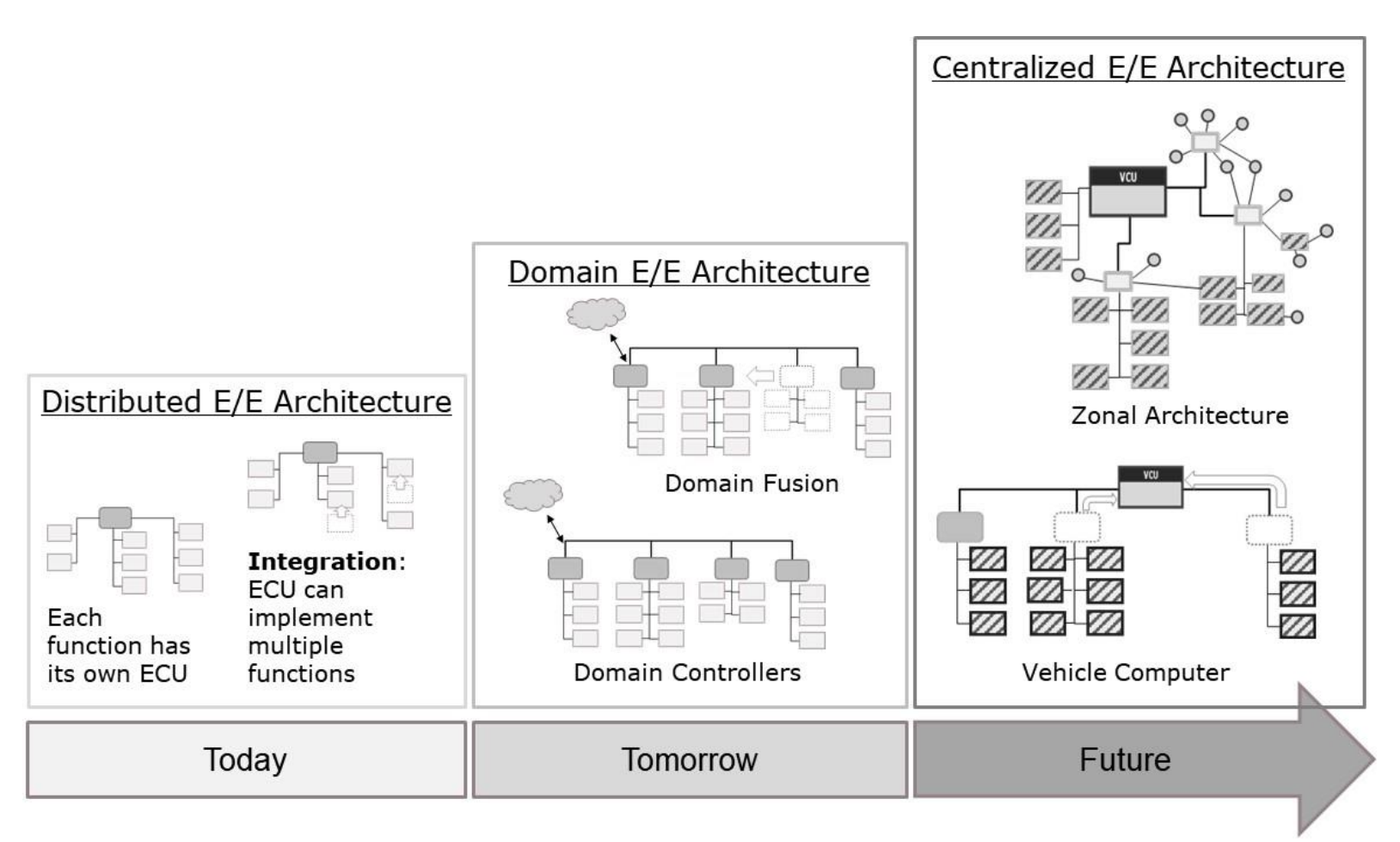
【算法】求{1,2,3}序列的全排列,邻里交换法(Java)
代码如下:
public class Main{static int count;static int a[]= {1,2,3};public static void main(String[] args) {f(a,0);System.out.println(count);}public static void f(int a[],int step) {if(step==a.length-1) {count++;return;}for(int i=step;i<a.length;i++) {{int x=a[i];//交换a[i]=a[step];a[step]=x;}f(a,step+1);{int x=a[i];//还原数据a[i]=a[step];a[step]=x;}}} }图解如下:
执行过程如下:这段代码实现了对数组
a中元素的全排列,并在count中记录排列的数量。下面是每一步的具体细节:
初始状态:
a[] = {1, 2, 3}count = 0调用
f(a, 0),进入函数f:
a[] = {1, 2, 3}step = 0进入
for循环,i = 0:
- 交换
a[0]和a[0](实际上没有变化)- 进入递归,调用
f(a, 1):
a[] = {1, 2, 3}step = 1进入
for循环,i = 1:
- 交换
a[1]和a[1](实际上没有变化)- 进入递归,调用
f(a, 2):
a[] = {1, 2, 3}step = 2
step == a.length - 1成立,执行count++:
count = 1返回上一层递归,恢复数组
a到初始状态:
a[] = {1, 2, 3}继续
for循环,i = 2:
- 交换
a[2]和a[1],得到a[] = {1, 3, 2}- 进入递归,调用
f(a, 2):
a[] = {1, 3, 2}step = 2
step == a.length - 1成立,执行count++:
count = 2返回上一层递归,恢复数组
a到初始状态:
a[] = {1, 2, 3}返回上一层递归,恢复数组
a到初始状态:
a[] = {1, 2, 3}继续
for循环,i = 1:
- 交换
a[1]和a[0],得到a[] = {2, 1, 3}- 进入递归,调用
f(a, 1):
a[] = {2, 1, 3}step = 1进入
for循环,i = 1:
- 交换
a[1]和a[1](实际上没有变化)- 进入递归,调用
f(a, 2):
a[] = {2, 1, 3}step = 2
step == a.length - 1成立,执行count++:
count = 3返回上一层递归,恢复数组
a到初始状态:
a[] = {2, 1, 3}继续
for循环,i = 2:
- 交换
a[2]和a[1],得到a[] = {2, 3, 1}- 进入递归,调用
f(a, 2):
a[] = {2, 3, 1}step = 2
step == a.length - 1成立,执行count++:
count = 4返回上一层递归,恢复数组
a到初始状态:
a[] = {2, 1, 3}返回上一层递归,恢复数组
a到初始状态:
a[] = {1, 2, 3}继续
for循环,i = 2:
- 交换
a[2]和a[0],得到a[] = {3, 2, 1}- 进入递归,调用
f(a, 1):
a[] = {3, 2, 1}step = 1进入
for循环,i = 1:
- 交换
a[1]和a[1](实际上没有变化)- 进入递归,调用
f(a, 2):
a[] = {3, 2, 1}step = 2
step == a.length - 1成立,执行count++:
count = 5返回上一层递归,恢复数组
a到初始状态:
a[] = {3, 2, 1}继续
for循环,i = 2:
- 交换
a[2]和a[1](实际上没有变化)- 进入递归,调用
f(a, 2):
a[] = {3, 2, 1}step = 2
step == a.length - 1成立,执行count++:
count = 6返回上一层递归,恢复数组
a到初始状态:
a[] = {3, 2, 1}返回上一层递归,恢复数组
a到初始状态:
a[] = {1, 2, 3}返回上一层递归,主函数结束。
最终输出
count的值为6,表示数组[1, 2, 3]