显然我们直接看前一半，然后我们按照斜行看，我们发现斜行是递增的，而同一行从左向右也是递增的，因此我们可以直接二分，同时我们发现对称轴的数为Ck,2k.

我们从16斜行枚举即可

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
int n;
LL C(int a,int b){LL res=1;for(int i=a,j=1;j<=b;i--,j++){res=res*i/j;if(res>n) return res;}return res;
}
bool check(int k){LL l=k*2,r=n;if(l>r) return 0;while(l<r){LL mid=l+r>>1;if(C(mid,k)>=n) r=mid;else l=mid+1;}if(C(r,k)!=n) return 0;cout<<(r+1)*r/2+k+1;return 1;
}
int main(){cin>>n;for(int k=16;;k--){if(check(k)){break;}}
}

2.spfa的本质（妙）

我们令f[i][j]表示在i步以内可以生成j作物的方法的集合，我们记录其最小时间，答案就是f[n-1][t]，对于初始值，f[0][xi]=0，对于f[i][j]，我们可以看看j的生成方式即可，即f[i][j]=min(f[i][j],max(f[i-1][x],f[i-1][y])),复杂度为(n-1)k,我们加个spfa思想优化，j是由x,y更新的，只有x,y更新j才可能更新，

下面是AC代码：

#include<bits/stdc++.h>
using namespace std;
const int N=2010,M=200010;
int n,m;
int h[N],e[M],w[N],target[M],ne[M],idx;
int dis[N];
queue<int> q;
bool st[N];
void add(int a,int b,int c){e[idx]=b,target[idx]=c,ne[idx]=h[a],h[a]=idx++;
}
void spfa(){while(q.size()){int x=q.front();q.pop();st[x]=0;for(int i=h[x];i!=-1;i=ne[i]){int y=e[i],z=target[i];if(dis[z]>max(dis[x],dis[y])+max(w[x],w[y])){dis[z]=max(dis[x],dis[y])+max(w[x],w[y]);if(!st[z]){q.push(z);st[z]=1;}}}}
}
int main(){int k,T;cin>>n>>m>>k>>T;memset(h,-1,sizeof(h));for(int i=1;i<=n;i++) scanf("%d",&w[i]);memset(dis,0x3f,sizeof(dis));while(m--){int x;scanf("%d",&x);dis[x]=0;q.push(x);st[x]=1;}while(k--){int a,b,c;scanf("%d%d%d",&a,&b,&c);add(a,b,c);add(b,a,c);}spfa();cout<<dis[T];
}

3.欧拉函数：

下面是数学推导：

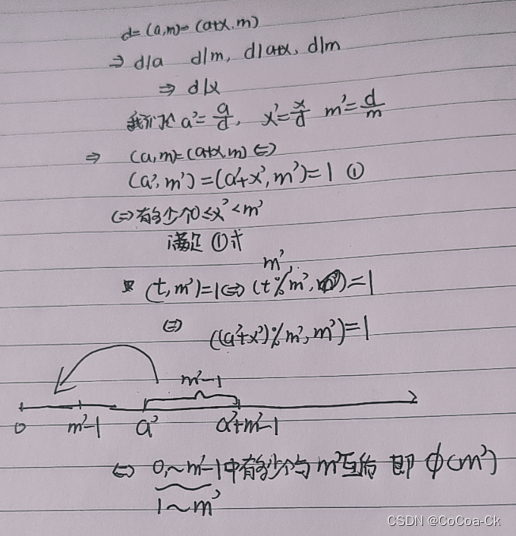
下面是AC代码：

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
LL gcd(LL a,LL b){return b?gcd(b,a%b):a;
}
LL phi(LL m){LL res=m;for(LL i=2;i<=m/i;i++){if(m%i==0){while(m%i==0) m/=i;res=res/i*(i-1);}}if(m>1) res=res/m*(m-1);return res;
}
int main(){int T;cin>>T;while(T--){LL a,m;cin>>a>>m;LL d=gcd(a,m);cout<<phi(m/d)<<endl;}
}