【三十六】【算法分析与设计】综合练习（3），39. 组合总和，784. 字母大小写全排列，526. 优美的排列

39. 组合总和

对每一个位置进行枚举

枚举每一个数出现的次数

784. 字母大小写全排列

526. 优美的排列

结尾

39. 组合总和

给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ，找出 candidates 中可以使数字和为目标数 target 的所有 不同组合 ，并以列表形式返回。你可以按 任意顺序 返回这些组合。

candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同，则两种组合是不同的。

对于给定的输入，保证和为 target 的不同组合数少于 150 个。

示例 1：
输入：candidates = [2,3,6,7], target = 7输出：[[2,2,3],[7]] 解释： 2 和 3 可以形成一组候选，2 + 2 + 3 = 7 。注意 2 可以使用多次。 7 也是一个候选， 7 = 7 。仅有这两种组合。

示例 2：
输入: candidates = [2,3,5], target = 8 输出: [[2,2,2,2],[2,3,3],[3,5]]

示例 3：
输入: candidates = [2], target = 1 输出: []

提示：

1 <= candidates.length <= 30

2 <= candidates[i] <= 40

candidates 的所有元素 互不相同

1 <= target <= 40

对每一个位置进行枚举

定义节点信息，定义path存储路径，定义sum存储当前节点的数字和。这两个变量表示一个节点位置。

定义pos表示孩子节点从哪个下表位置开始枚举。223和322是同一种情况，也就是当排序好了的序列只会出现一次。因此子树每一次都是从根节点的数字开始枚举。这样保证枚举的情况都是非递减，也就保证的不重复。

定义ret存储结果序列。

递归出口，如果sum==aim，将path加入ret结果序列中，return。

剪枝，如果sum>aim，不需要再枚举，直接返回return。

递归遍历整个树。

对于每一棵树根节点，遍历整个树相当于遍历该节点所有的子树。

class Solution {
public:vector<vector<int>> ret;vector<int> path;int sum = 0;int aim;vector<vector<int>> combinationSum(vector<int>& nums, int target) {aim = target;dfs(nums, 0);return ret;}void dfs(vector<int>& nums, int pos) {if (sum == aim) {ret.push_back(path);return;}if (sum > aim)return;for (int i = pos; i < nums.size(); i++) {path.push_back(nums[i]);sum = sum + nums[i];dfs(nums, i);path.pop_back();sum = sum - nums[i];}}
};

将全局遍历int类型写到递归函数作为非引用参数，此时不需要再手动回溯，提高效率。

但是不将vector类型写到递归函数作为非引用参数，因为每一次都需要开辟vector的空间，效率反而可能下降。

但是每次开辟int类型的空间，效率影响比较小。

class Solution {
public:vector<vector<int>> ret;vector<int> path;int aim;vector<vector<int>> combinationSum(vector<int>& nums, int target) {aim = target;dfs(nums, 0, 0);return ret;}void dfs(vector<int>& nums, int pos, int sum) {if (sum == aim) {ret.push_back(path);return;}if (sum > aim)return;for (int i = pos; i < nums.size(); i++) {path.push_back(nums[i]);dfs(nums, i, sum + nums[i]);path.pop_back();}}
};

枚举每一个数出现的次数

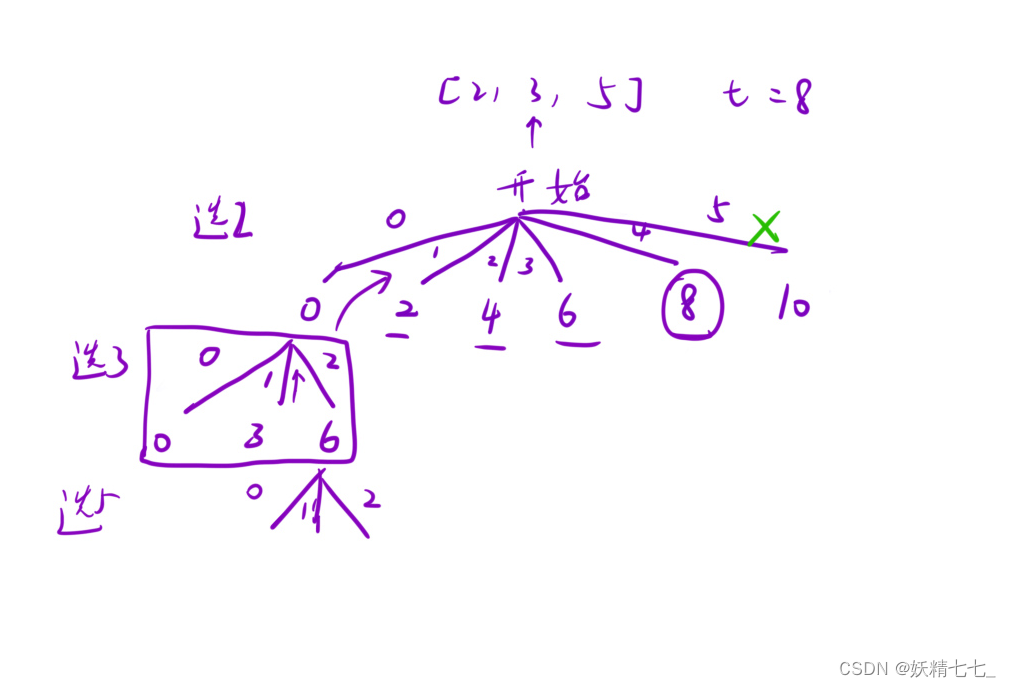
这种情况的剪枝操作多了一个，就是当pos孩子枚举的位置是nums.size()，此时不需要再继续下去了。

class Solution {
public:vector<vector<int>> ret;vector<int> path;int aim;vector<vector<int>> combinationSum(vector<int>& nums, int target) {aim = target;dfs(nums, 0, 0);return ret;}void dfs(vector<int>& nums, int pos, int sum) {if (sum == aim) {ret.push_back(path);return;}if (sum > aim || nums.size() == pos)return;for (int i = 0; i * nums[pos] <= aim; i++) {if (i)path.push_back(nums[pos]);dfs(nums, pos + 1, sum + i * nums[pos]);}for (int i = 1; i * nums[pos] <= aim; i++)path.pop_back();}
};

784. 字母大小写全排列

给定一个字符串 s ，通过将字符串 s 中的每个字母转变大小写，我们可以获得一个新的字符串。

返回 所有可能得到的字符串集合 。以 任意顺序 返回输出。

示例 1：

输入：s = "a1b2" 输出：["a1b2", "a1B2", "A1b2", "A1B2"]

示例 2:

输入: s = "3z4" 输出: ["3z4","3Z4"]

提示:

1 <= s.length <= 12

s 由小写英文字母、大写英文字母和数字组成

定义path表示节点的序列。

定义pos表示下一个可能出现的字符，也就是对应孩子节点的选取。

递归函数遍历整个树。

递归出口，path.size()==s.size()。

class Solution {
public:vector<string> ret;string path;vector<string> letterCasePermutation(string s) {dfs(s, 0);return ret;}void dfs(string& s, int pos) {if (path.size() == s.size()) {ret.push_back(path);return;}// 变if (s[pos] > '9' || s[pos] < '0') {path.push_back(change(s[pos]));dfs(s, pos + 1);path.pop_back();}// 不变path.push_back(s[pos]);dfs(s, pos + 1);path.pop_back();}char change(char& ch) {if (ch <= 'z' && ch >= 'a')return ch - 32;elsereturn ch + 32;}
};

526. 优美的排列

假设有从 1 到 n 的 n 个整数。用这些整数构造一个数组 perm（下标从 1 开始），只要满足下述条件之一，该数组就是一个 优美的排列 ：

perm[i] 能够被 i 整除

i 能够被 perm[i] 整除

给你一个整数 n ，返回可以构造的 优美排列 的数量。

示例 1：

输入：n = 2 输出：2 解释： 第 1 个优美的排列是 [1,2]： - perm[1] = 1 能被 i = 1 整除 - perm[2] = 2 能被 i = 2 整除第 2 个优美的排列是 [2,1]: - perm[1] = 2 能被 i = 1 整除 - i = 2 能被 perm[2] = 1 整除

示例 2：

输入：n = 1 输出：1

提示：

1 <= n <= 15

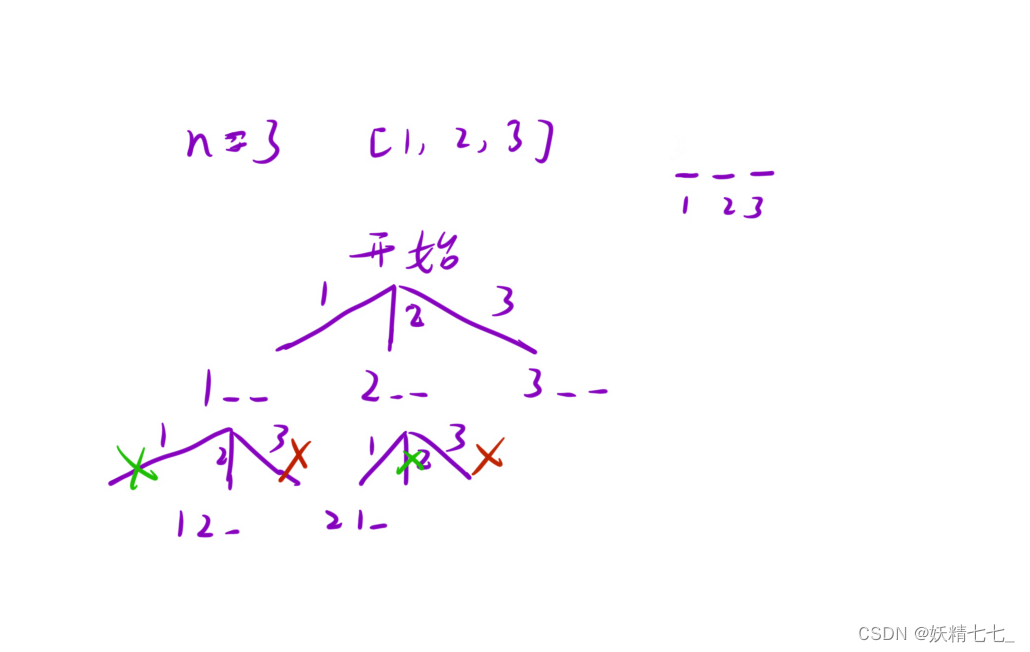
定义ret存储结果个数。

定义check存储当前节点之前已经使用的数字。

定义pos表示孩子节点枚举的位置。

每一个节点都需要维护这一节点的定义。也就是回溯。

class Solution {
public:int ret;vector<bool> check;int countArrangement(int n) {check.resize(16);dfs(1, n);return ret;}void dfs(int pos, int n) {if (pos == n + 1) {ret++;return;}for (int i = 1; i <= n; i++) {if (!check[i] && (i % pos == 0 || pos % i == 0)) {check[i] = true;dfs(pos + 1, n);check[i] = false;}}}
};