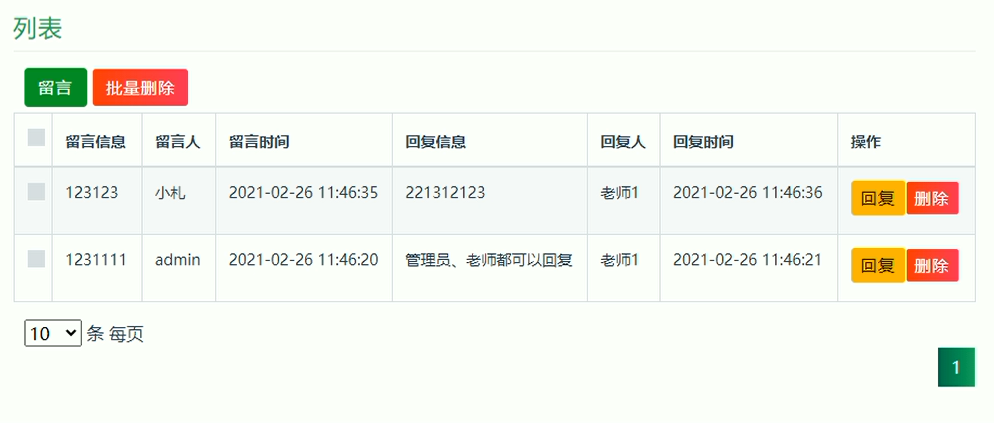
一:动态规划概述:
动态规划实际上是一种将原本的 '大' 方面的问题转化为许许多多的 '小方面' 的一种应用, 在一定程度上避免数据的重复, 并且能够将数据以自己希望的方式进行存储, 用来解决多阶段的数学问题, 从而提高算法的效率
在算法当中, 动态规划主要包括有:
递推, 线性DP 记忆化搜索 背包问题 属性DP 区间DP 数位DP 状压DP 几种算法
二.背包问题:
背包问题动态规划的一种, 这里我们重点讲解背包问题
1.发现背包问题:
背包问题往往都比较容易观察出来, 即给出总的容量, 以及物品的总数, 之后输入物品的价值以及占用容量, 求对空间的最大利用价值......本题当中也是类似的
2."规划"背包
在发现这一类是背包问题之后, 我们就可以开始着手整理"背包"的模板(几乎这类问题的基础模板都是彼此类似的)
在做题之前, 我们先以简单的例子来初步理解背包的构造
同时, 之后对于这类型的题目, 我们都可以使用表格来帮助我们更好的去理解
2.1> 例子:
背包总的容量是8 装入4个物品 所有物品只能够放一次
物品1 2WEIGHT 3VALUE
物品2 3WEIGHT 4VALUE
物品3 4WEIGHT 5VALUE
物品4 5WEIGHT 6VALUE
第二个数字代表其重量, 第三个代表这个物品的价值
2.2>创建背包
我们规定最左边的一列代表物品, 最上边的一行代表的是这个背包的容量(0~8)

并且由于第0个物品时不存在的, 所以第一行的各种背包都不存放, 价值都为0, 同样的, 第一列因为容量为0, 所以任何的物品都装不下, 也都为0

当我们来到物品为1, 背包容量为2的时候, 我们发现已经可以装进去物品1了, 这个时候其价值应当为3

继续向下进行填写, 来到了另外一个转折点, 背包容量为3的时候, 我们发现容量为3的物品2能够装进去
能够装进去之后, 我们还需要考虑两种情况:
①:能装但不装进去
②:能装并且装进去
对于第一种情况, 如果不装进去, 那么跟上一行的最大价值应该时一样的
对于第二种情况, 如果装进去了, 那么其价值应该时当前物品的价值, 加上剩余容量能装的最大价值, 也需要我们返回上一行去寻找
这两种情况我们都需要考虑, 并且选出其中最大的一个作为当前的容纳量的最大价值(毕竟单个价值大的不一定比单个价值小数量多的价值和大~~~~)
以物品2 容量为3举例:
①:不装进去, 跟上一行的价值一样为 3
②:装进去, 物品2价值为4 装了物品2之后的剩余容量为0, 对应价值为0 所以最大价值就是 4 + 0 =4
两者相互比较, 发现装进去的价值大, 我们就选择填入 4
依照上面的方法, 我们得到最终的表单

2.3>创建"数据"背包
在了解过外层原理了之后, 我们开始构建代码版本的背包, 表格的形式也让人自然的想起了二维数组, 没茅台!
使用二维数组, 我们存放N个物品, 每一个物品有0~W的重量背包
也就是:
int[] dp = new int[N+1][W+1]
加一是因为我们在索引为0处不存放任何数据, 让其默认值为0即可
再加上一些循环的操作, 我们就能够实现这个 "数据背包"
这里, 我们以values[] 和 weight[] 接收对应的价值以及重量
2.4.梳理思路:
两大类+两小类组合方式
一:物品weight[i]比当前的容量大, 无法装进去
二:物品weight[i]小于等于当前容量, 可以装进去
1.能够装但是不装进去:
如果不装进去, 那么跟上一行的最大价值应该时一样的
即dp[i][i1]=dp[i-1][i1]
2.能够装并且装进去:
如果装进去了, 那么其价值应该时当前物品的价值, 加上剩余容量能装的最大价值, 也需要我们返回上一行去寻找
即dp[i][i1]=max(dp[i-1][i1],weight[i]+dp[i-1][i1-weight[i]]);
整体的背包构建方式代码:
for (int i = 1; i < dp.length; i++) {for (int i1 = 0; i1 < dp[i].length; i1++) {
// 装不进去if(weights[i]>i1){dp[i][i1]=dp[i-1][i1];}
// 可以装进去else {dp[i][i1]=max(dp[i-1][i1],values[i]+dp[i-1][i1-weights[i]]);}}}三.当堂训练:
上案例:
这里我们以洛谷P1048为一个基础案例:
P1048 [NOIP2005 普及组] 采药 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)![]() https://www.luogu.com.cn/problem/P1048
https://www.luogu.com.cn/problem/P1048
题目描述
辰辰是个天资聪颖的孩子,他的梦想是成为世界上最伟大的医师。为此,他想拜附近最有威望的医师为师。医师为了判断他的资质,给他出了一个难题。医师把他带到一个到处都是草药的山洞里对他说:“孩子,这个山洞里有一些不同的草药,采每一株都需要一些时间,每一株也有它自身的价值。我会给你一段时间,在这段时间里,你可以采到一些草药。如果你是一个聪明的孩子,你应该可以让采到的草药的总价值最大。”
如果你是辰辰,你能完成这个任务吗?
输入格式
第一行有 22 个整数 T和M,用一个空格隔开,T 代表总共能够用来采药的时间,M 代表山洞里的草药的数目。
接下来的 M 行每行包括两个在 11 到 100100 之间(包括 11 和 100100)的整数,分别表示采摘某株草药的时间和这株草药的价值。
输出格式
输出在规定的时间内可以采到的草药的最大总价值。
输入 #1
70 3 71 100 69 1 1 2
输出 #1
3
最后附上答案, 好孩子都是自己先做再看题解的哦>*<
import java.util.*;import static sun.swing.MenuItemLayoutHelper.max;public class p1048 {public static void main(String[] args) {Scanner in =new Scanner(System.in);int T=in.nextInt();int M=in.nextInt();
// T代表时间 -- > 背包总重量 M代表个数
// 问题实际上是一个背包问题, 可以采用二维数组的方式int[] times=new int[M+1];int[] values=new int[M+1];for (int i = 1; i <=M; i++) {int time=in.nextInt();int value=in.nextInt();times[i]=time;values[i]=value;}
// 使用二维数组进行接收int[][] end=new int[M+1][T+1];
// 开始进行背包问题的循环for (int i = 1; i < end.length; i++) {for (int i1 = 0; i1 < end[i].length; i1++) {
// 一.第一种情况,判断是否够装进去if(times[i]>i1){end[i][i1]=end[i-1][i1];}else {end[i][i1]=max(values[i]+end[i-1][i1-times[i]],end[i-1][i1]);}}}System.out.println(end[M][T]);}
}