理论基础
刷题大纲:

动态规划5步曲:
1、确定dp数组以及下标的含义
2、确定递推公式
3、dp数组如何初始化
4、确定遍历顺序
5、举例推导dp数组
509. 斐波那契数
509. 斐波那契数 - 力扣(LeetCode)
代码随想录 (programmercarl.com)
手把手带你入门动态规划 | LeetCode:509.斐波那契数_哔哩哔哩_bilibili
斐波那契数 (通常用
F(n)表示)形成的序列称为 斐波那契数列 。该数列由0和1开始,后面的每一项数字都是前面两项数字的和。也就是:F(0) = 0,F(1) = 1 F(n) = F(n - 1) + F(n - 2),其中 n > 1给定
n,请计算F(n)。示例 1:
输入:n = 2 输出:1 解释:F(2) = F(1) + F(0) = 1 + 0 = 1示例 2:
输入:n = 3 输出:2 解释:F(3) = F(2) + F(1) = 1 + 1 = 2示例 3:
输入:n = 4 输出:3 解释:F(4) = F(3) + F(2) = 2 + 1 = 3提示:
0 <= n <= 30
动规五部曲:
用一个一维dp数组来保存递归的结果:
1、确定dp数组以及下标的含义
dp[i]的定义为:第i个数的斐波拉契值是dp[i]
2、确定递归公式:
这道题的公式:dp[i]=dp[i-1]+dp[i-2]
3、dp数组如何初始化:
该题:dp[0]=0; dp[1]=1
4、确定遍历顺序:后一个数的值依赖于前一个数的值,所以遍历的顺序应该是从前往后
for(int index = 2; index <= n; index++){}5、举例子推导dp数组:
当n为10,dp数组应该是如下的数列:0 1 1 2 3 5 8 13 21 34 55;写完代码之后可以手动带入看一下结果是否正确
综合代码:
// 非压缩状态的版本
class Solution {public int fib(int n) {if (n <= 1) return n; // 如果 n 小于等于 1,直接返回 nint[] dp = new int[n + 1]; // 创建一个数组 dp,长度为 n+1dp[0] = 0; // dp 数组的第一个元素为 0dp[1] = 1; // dp 数组的第二个元素为 1for (int index = 2; index <= n; index++){ // 循环从 2 到 ndp[index] = dp[index - 1] + dp[index - 2]; // 计算 Fibonacci 数列的第 index 项并存储到 dp 数组中}return dp[n]; // 返回 Fibonacci 数列的第 n 项}
}
70. 爬楼梯
70. 爬楼梯 - 力扣(LeetCode)
代码随想录 (programmercarl.com)
带你学透动态规划-爬楼梯(对应力扣70.爬楼梯)| 动态规划经典入门题目_哔哩哔哩_bilibili
假设你正在爬楼梯。需要
n阶你才能到达楼顶。每次你可以爬
1或2个台阶。你有多少种不同的方法可以爬到楼顶呢?示例 1:
输入:n = 2 输出:2 解释:有两种方法可以爬到楼顶。 1. 1 阶 + 1 阶 2. 2 阶示例 2:
输入:n = 3 输出:3 解释:有三种方法可以爬到楼顶。 1. 1 阶 + 1 阶 + 1 阶 2. 1 阶 + 2 阶 3. 2 阶 + 1 阶提示:
1 <= n <= 45
n=2,输出2;n=3,输出3;n=4,输出5..... 可以发现5=3+2, 这道题和上一道斐波拉契的解法相同。
动规五部曲:
定义一个一维数组来记录每级台阶的状态;
1、确定dp以及下标的含义:dp[i]: 爬到第i层楼,有dp[i]种方法;
2、确定递推公式:
从dp[i]的定义可以看出,dp[i] 可以有两个方向推出来。
首先是dp[i - 1],上i-1层楼梯,有dp[i - 1]种方法,那么再一步跳一个台阶不就是dp[i]了么。
还有就是dp[i - 2],上i-2层楼梯,有dp[i - 2]种方法,那么再一步跳两个台阶不就是dp[i]了么。
那么dp[i]就是 dp[i - 1]与dp[i - 2]之和!
所以dp[i] = dp[i - 1] + dp[i - 2] 。
3、dp数组如何初始化:dp[1] = 1,dp[2] = 2
4、确定遍历顺序:和斐波拉契一样,从前往后
5、举例推导dp数组:当n=5:
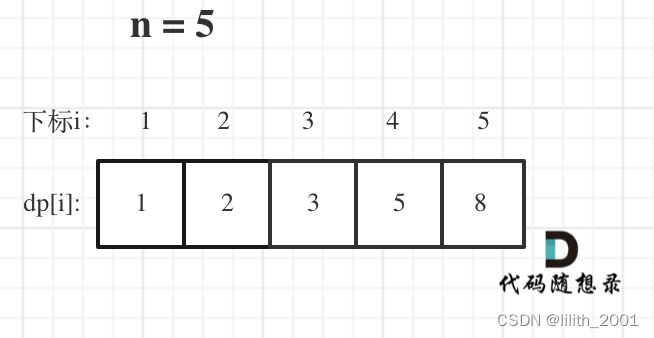
综合代码:
// 用变量记录代替数组
class Solution {public int climbStairs(int n) {if(n <= 2) return n;int a = 1, b = 2, sum = 0;for(int i = 3; i <= n; i++){sum = a + b; // f(i - 1) + f(i - 2)a = b; // 记录f(i - 1),即下一轮的f(i - 2)b = sum; // 记录f(i),即下一轮的f(i - 1)}return b;}
}以上代码中,迭代过程如下:
初始状态:
a = 1
b = 2
sum = 0第一次迭代:
a = 1
b = 2
sum = a + b = 1 + 2 = 3第二次迭代:
a = b = 2
b = sum = 3
sum = a + b = 2 + 3 = 5第三次迭代:
a = b = 3
b = sum = 5
sum = a + b = 3 + 5 = 8以此类推...