目录
x进制减法
数组切分
gcd
青蛙过河
x进制减法

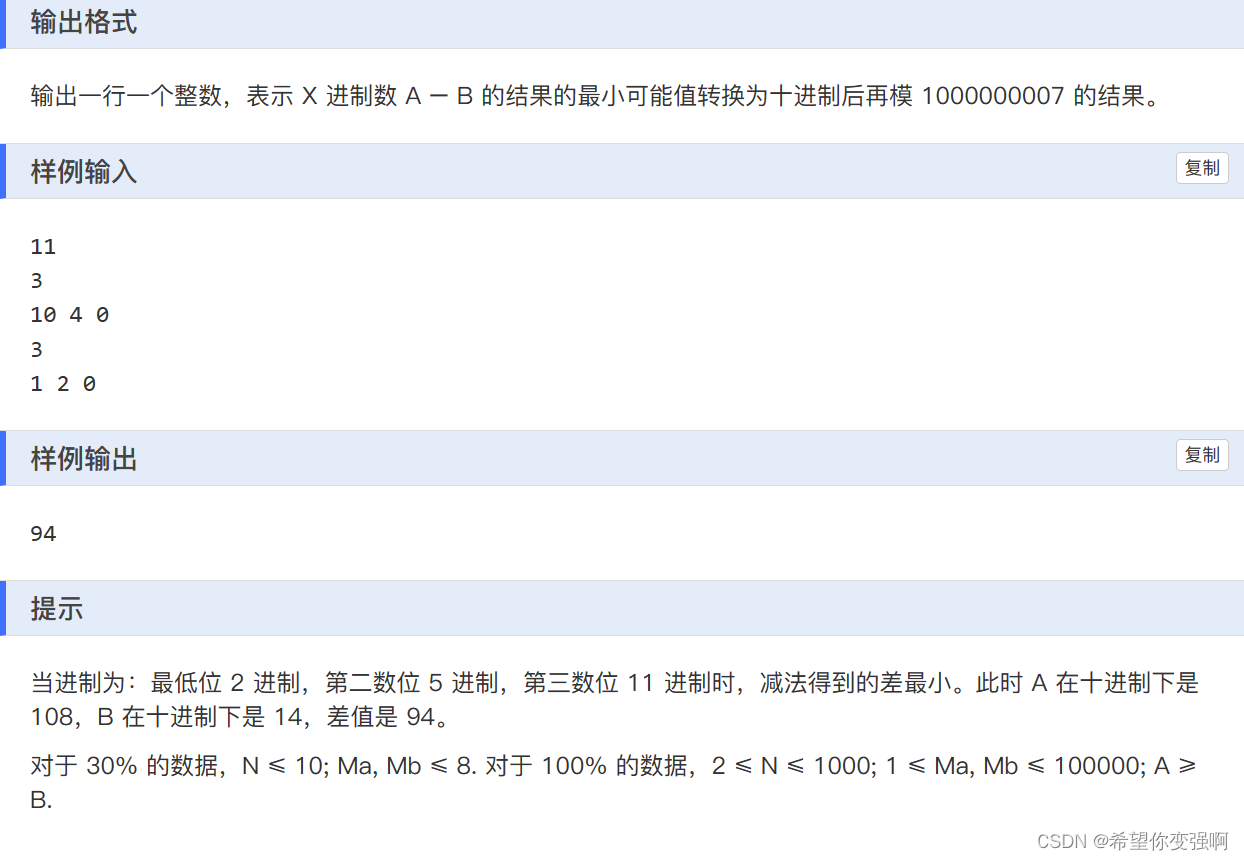
其实就是一道观察规律的题。你发现如果a这个位置上的数x,b这个位置上的数是y,那么此位置至少是max(x,y)+1进制。一定要把位置找对啊
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll N=1e5+10,mod=1000000007;
int len1,len2;
ll tmp,ans,a[N],b[N],c[N],n;
int main(){cin>>n;cin>>len1;for(int i=len1;i>=1;i--)cin>>a[i];cin>>len2;for(int i=len2;i>=1;i--)cin>>b[i];for(int i=len1;i>=1;i--){c[i]=max(max(a[i]+1,b[i]+1),2*1ll);a[i]=a[i]-b[i];}tmp=1;for(int i=1;i<=len1;i++){ans=(tmp*a[i]+ans)%mod;tmp=(tmp*c[i])%mod;}cout<<ans;return 0;
}
/*错解
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll N=1e5+10,mod=1000000007;
int len1,len2;
ll tmp,ans,a[N],b[N],c[N],n;
int main(){cin>>n;cin>>len1;for(int i=1;i<=len1;i++)cin>>a[i];cin>>len2;for(int i=1;i<=len2;i++)cin>>b[i];for(int i=1;i<=len1;i++){c[i]=max(max(a[i]+1,b[i]+1),2*1ll);a[i]=a[i]-b[i];//这个bug我找了两个小时,不能从高位开始减,}tmp=1;for(int i=len1;i>=1;i--){ans=(tmp*a[i]+ans)%mod;tmp=(tmp*c[i])%mod;}
cout<<ans;return 0;
}*/
数组切分
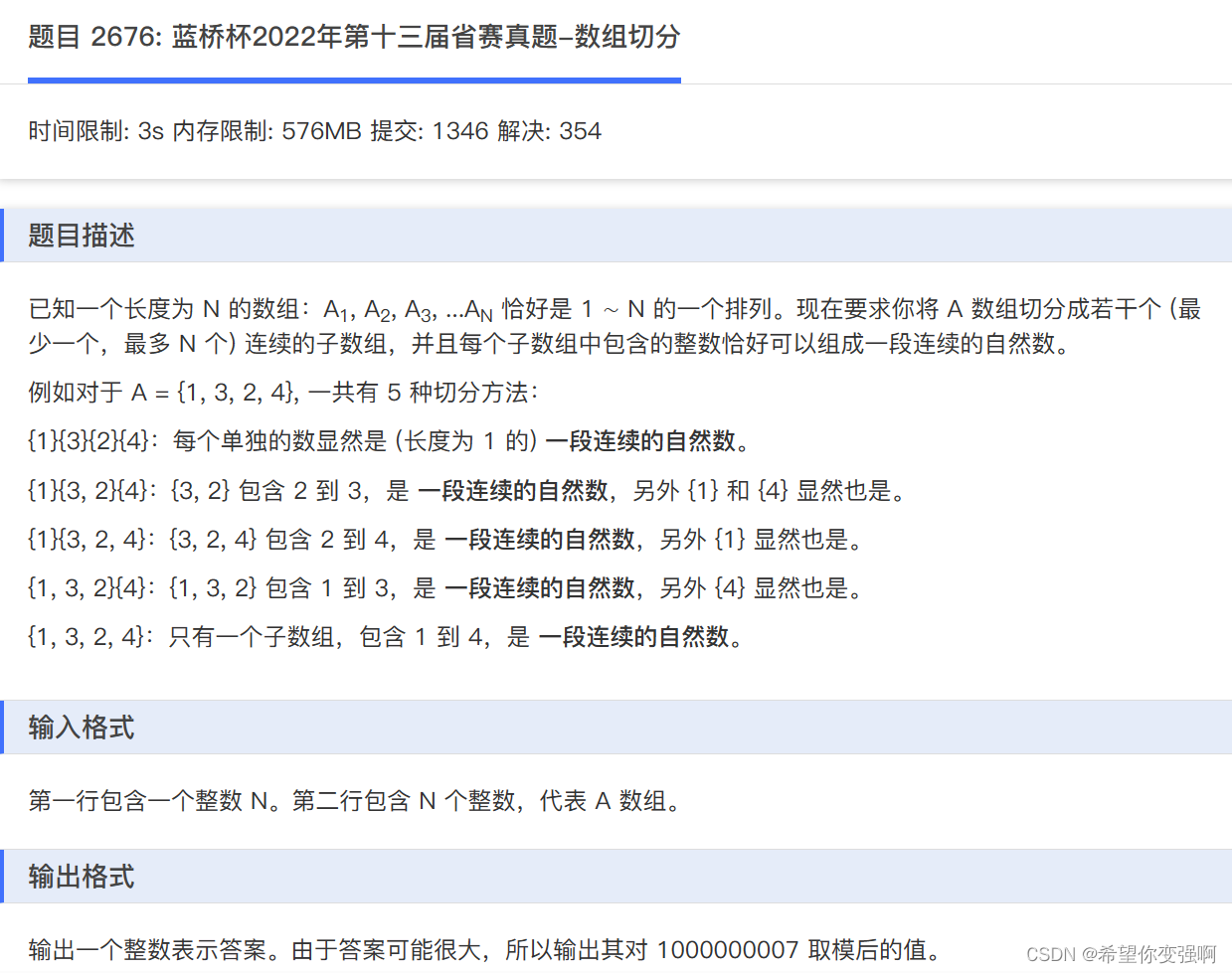
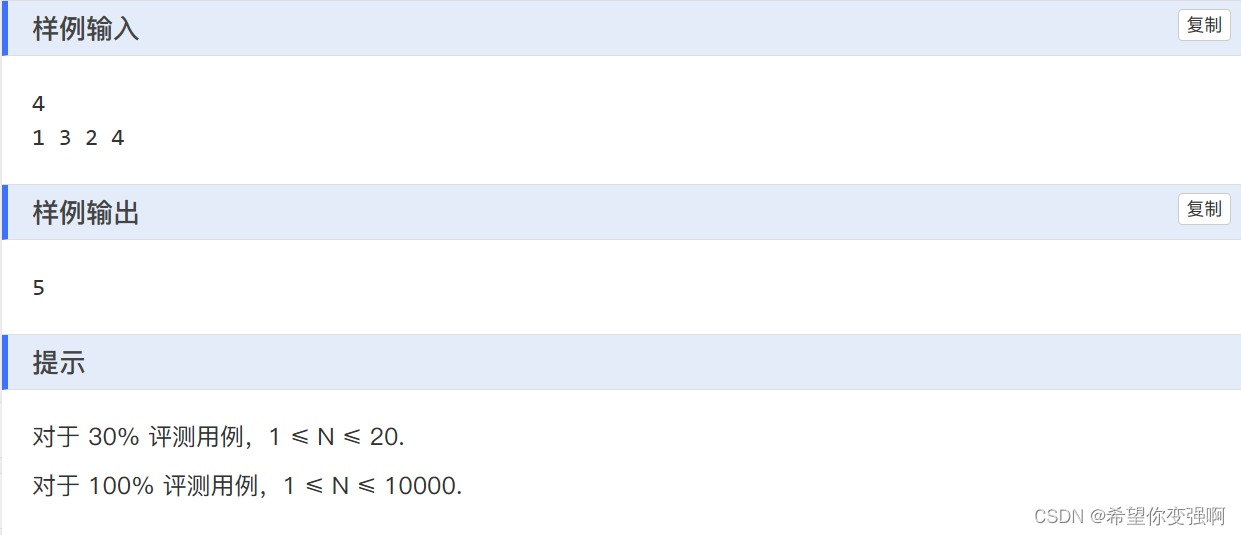
一道动态规划题,
我们设置f[i]表示从1到i区间的切法。那么可以从任意区间[j,i]转移,只要这个区间[j,i]也是满足题意的就行。那么如果判断[j,i]是否满足题意呢?
首先要注意到题上给出的是连续的的1~n的某个排列,然后我们只需要判断区间的极值和区间长度是否一样就行,如果相等,就说明此区间一定是连续的自然数。
#include <bits/stdc++.h>
using namespace std;
long long f[10010],mod =1000000007;
int a[10010],n;
int main(){cin>>n;for(int i=1;i<=n;i++)cin>>a[i];f[0]=1;for(int i=1;i<=n;i++){int ma=a[i],mi=a[i];for(int j=i;j>=1;j--){ma=max(ma,a[j]);mi=min(mi,a[j]);if(i-j==ma-mi){f[i]=(f[i]+f[j-1])%mod;}}}cout<<f[n];return 0;
}
gcd
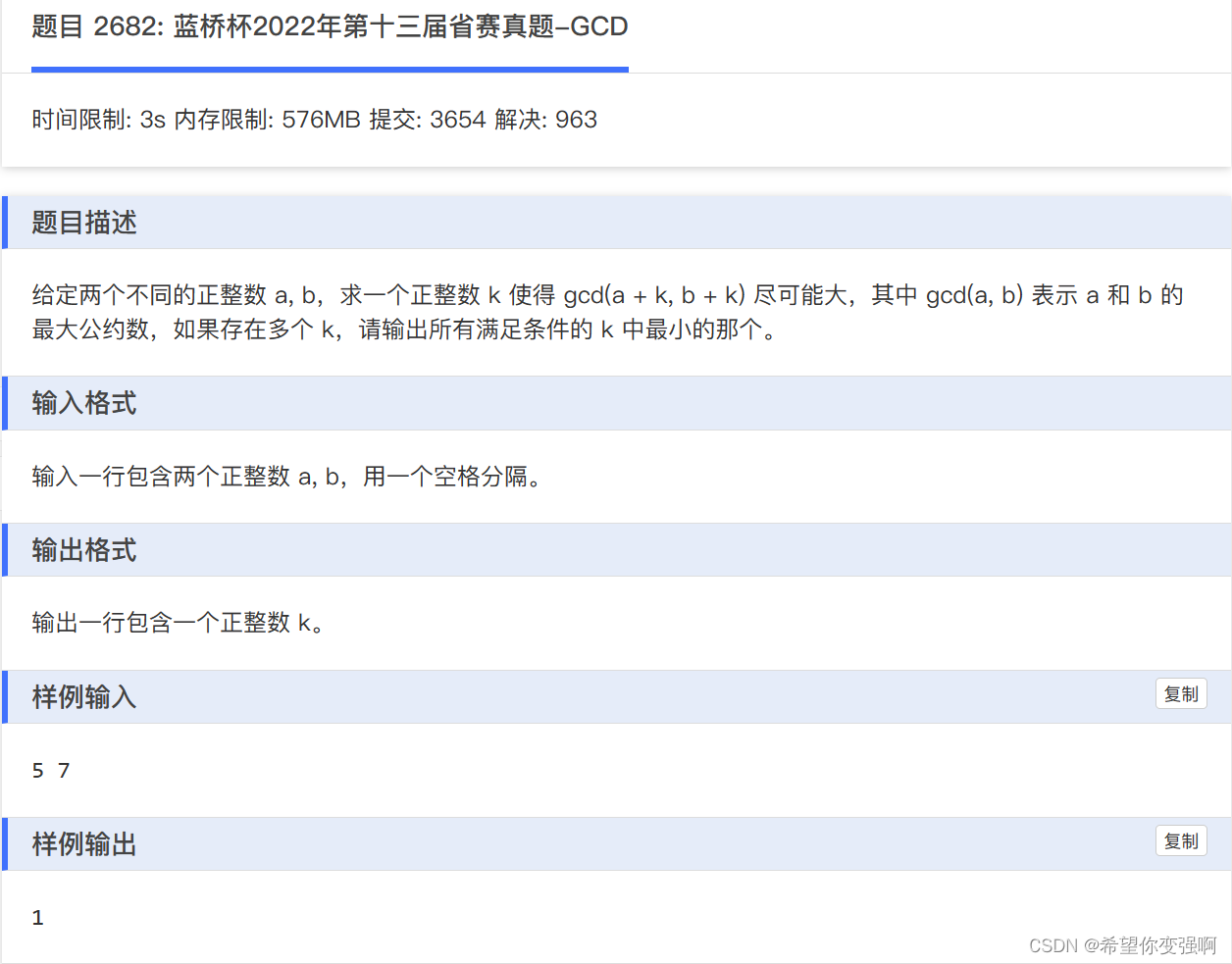

这道题本以为很麻烦,但是做着做着就发现了个不可思议的规律。
观察5和7,它们的最大gcd一定是2,为什么呢?因为你5+k和7+k始终保持差2,所以它们不可能有比2更大的gcd(因为它们两个一定是不等的)
对于一组a和b(假设b大于a),不妨另c=b-a。最终的a+k和b+k一定是差c,而且c必是它们的公因数。所以如果b+k是m*c的话,那么此时a+k必然也是c的倍数(因为它们两个差c啊),所以只需要枚举到b的下一个c的倍数即可,也就是(b/c+1)*c
验证5和9,它们差值为4,我们枚举到8和12时候发现gcd已经是4了,那么k就确定了
验证2和9,它们差值为7,我们一直枚举到7和14时发现gcd为7,那么此时k也确定了
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll a,b,s,c;
int main(){cin>>a>>b;c=abs(a-b);if(a>b)swap(a,b);s=b/c;cout<<(s+1)*c-b;return 0;
}
青蛙过河
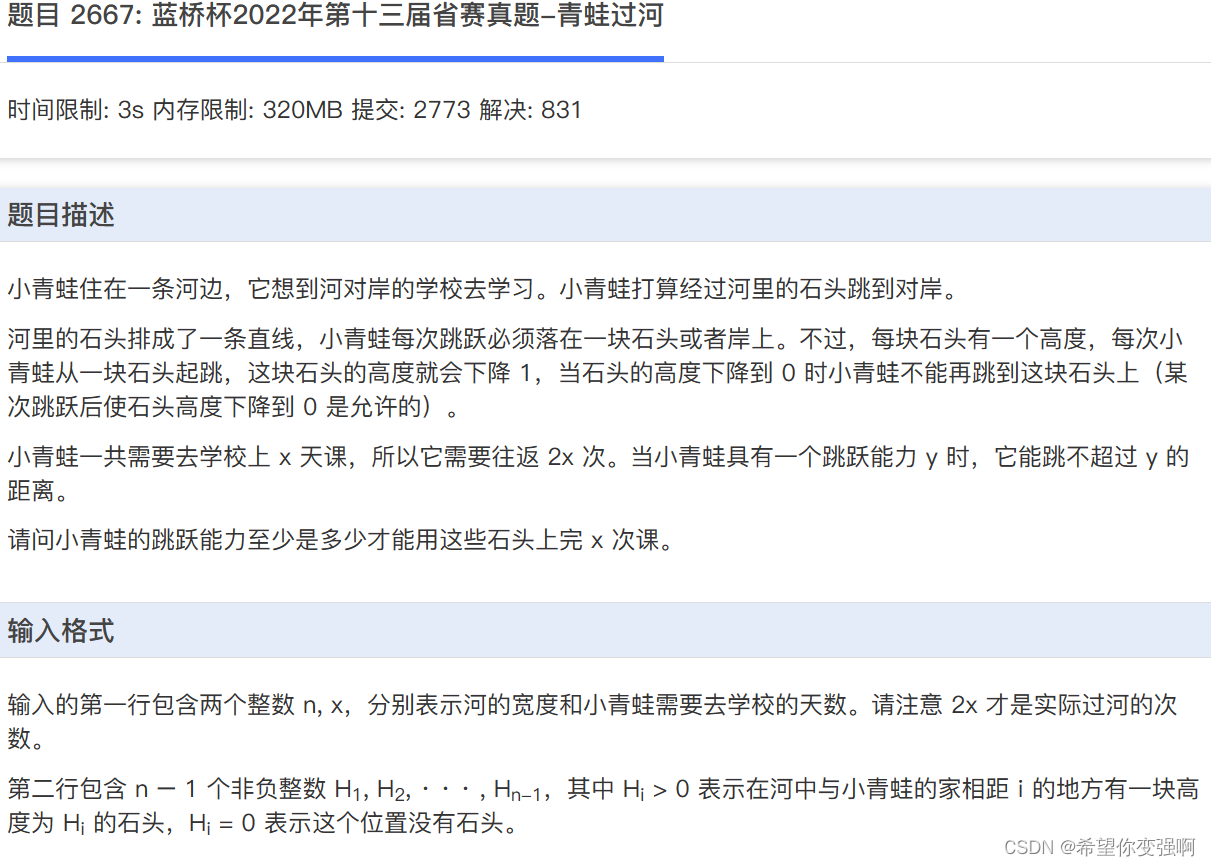

二分做法:
我们对跳跃距离二分,然后去判断这个距离能不能跑2x次即可,既然我们都已经确定了区间长度了。
那么不妨我们把这整个长度分成等长的mid区间,只需要保证所有的mid长度区间和都是大于2x的就行。
证明:(我只会反证法)
假设存在一组mid长度的区间和小于2x,那么经过x次来回,必然要经过此区间2x次,所以不成立。故原假设成立。
#include <bits/stdc++.h>
using namespace std;
const int N=1e5+10;
typedef long long ll;
int s[N];
ll n,x;
bool check(int m){for(int i=1;i+m<=n;i++){if(s[i+m-1]-s[i-1]<2*x) return false;}return true;
}
int main(){cin>>n>>x;int a;for(int i=1;i<n;i++)cin>>a,s[i]=s[i-1]+a;int l=1,r=n;while(l<=r){int mid=(l+r)>>1;if(check(mid)) r=mid-1;else l=mid+1;}cout<<l;return 0;
}