😎 作者介绍:我是程序员行者孙,一个热爱分享技术的制能工人。计算机本硕,人工制能研究生。公众号:AI Sun,视频号:AI-行者Sun
🎈 本文专栏:本文收录于《深入浅出算法》系列专栏,相信一份耕耘一份收获,我会系统全面的分享算法课程,届时可以拳打字节,脚踢腾讯
🤓 欢迎大家关注其他专栏,我将分享Web前后端开发、人工智能、机器学习、深度学习从0到1系列文章。
🖥 随时欢迎您跟我沟通,一起交流,一起成长、进步!

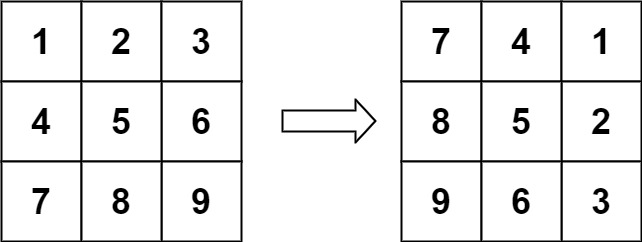
给定一个 n × n 的二维矩阵
matrix表示一个图像。请你将图像顺时针旋转 90 度。你必须在 原地 旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。
示例 1:
输入:matrix = [[1,2,3],[4,5,6],[7,8,9]] 输出:[[7,4,1],[8,5,2],[9,6,3]]示例 2:
输入:matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]] 输出:[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]提示:
n == matrix.length == matrix[i].length1 <= n <= 20-1000 <= matrix[i][j] <= 1000
思路一(正常思路,也是leetcode解法):

对于矩阵中第 i 行的第 j 个元素,在旋转后,它出现在倒数第 i 列的第 j 个位置。
void rotate(vector<vector<int>>& matrix) {auto temp=matrix;int n=matrix.size(),m=matrix[0].size();for(int i=0;i<n;i++)for(int j=0;j<m;j++)temp[j][n-i-1]=matrix[i][j]; matrix=temp;}思路二:原地操作(详细注释)
1.首先,我们遍历矩阵的上半部分行,用变量 i 迭代。
2.在每一行中,我们遍历矩阵的左半部分列,用变量 j 迭代。
3.对于每个元素 (i, j),我们将其旋转到正确的位置。具体而言,我们使用一个临时变量 temp 来保存当前元素的值。
4.然后,我们将当前元素移动到其在旋转后应该所在的位置。这涉及到四个位置的交换
- 将右上角的元素 (i, j) 移动到左上角 (i, n - j - 1)
- 将右下角的元素 (n - j - 1, i) 移动到右上角 (i, n - j - 1)
- 将左下角的元素 (n - i - 1, n - j - 1) 移动到右下角 (n - j - 1, i)
- 将左上角的元素 (j, n - i - 1) 移动到左下角 (n - i - 1, n - j - 1)
5.重复这个过程,直到完成所有位置的交换,实现了整个矩阵的旋转操作。
class Solution {
public:void rotate(vector<vector<int>>& matrix) {int n = matrix.size(); // 获取矩阵的大小for (int i = 0; i < n / 2; ++i) { // 遍历矩阵的上半部分行for (int j = 0; j < (n + 1) / 2; ++j) { // 遍历矩阵的左半部分列int temp = matrix[i][j]; // 保存当前元素的值matrix[i][j] = matrix[n - j - 1][i]; // 将右上角的元素移动到左上角matrix[n - j - 1][i] = matrix[n - i - 1][n - j - 1]; // 将右下角的元素移动到右上角matrix[n - i - 1][n - j - 1] = matrix[j][n - i - 1]; // 将左下角的元素移动到右下角matrix[j][n - i - 1] = temp; // 将左上角的元素移动到左下角}}}
};
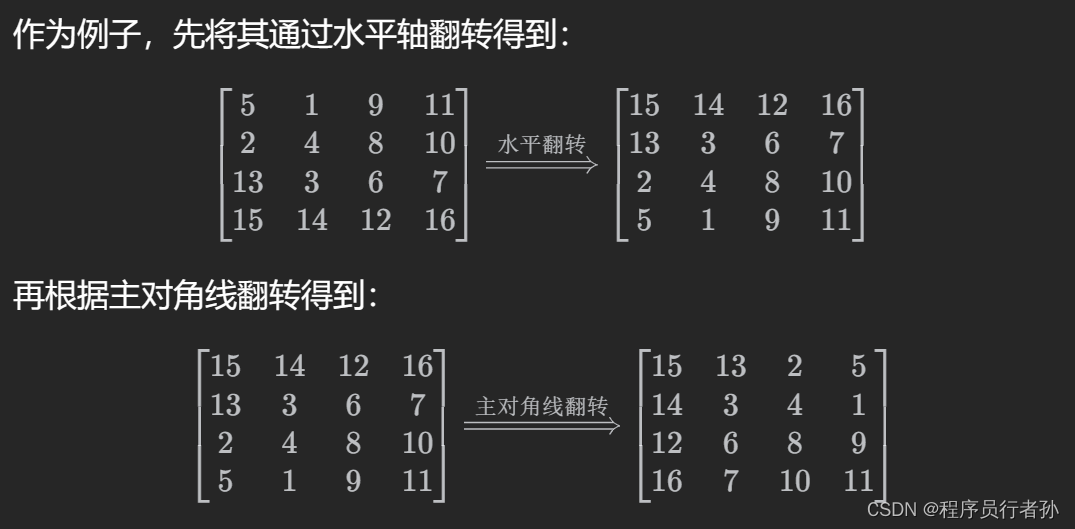
思路三: 翻转代替旋转
class Solution {
public:void rotate(vector<vector<int>>& matrix) {int n = matrix.size();// 水平翻转for (int i = 0; i < n / 2; ++i) {for (int j = 0; j < n; ++j) {swap(matrix[i][j], matrix[n - i - 1][j]);}}// 主对角线翻转for (int i = 0; i < n; ++i) {for (int j = 0; j < i; ++j) {swap(matrix[i][j], matrix[j][i]);}}}
};