D. Divisible Pairs

给出数组$a$，如果二元组$(i,j)$满足$a_i+a_{j}modx==0\&\&a_i-a_{j}mody==0$，则beauty。其中$i<j$

根据题意不难得出，符合条件的二元组应满足
$$\begin{gathered} a_i\mathrm{mod}x+a_j\mathrm{mod}x=x \\ {a}_i\mathrm{mod}y=a_j\mathrm{mod}y \end{gathered}$$

所以用$(a_i\mathrm{mod}x,a_i\mathrm{mod}y)$作为key，对于每个元素$a_i$查找$(x-a_i\mathrm{mod}x,a_i\mathrm{mod}y)$的个数

#include <iostream>
#include <string.h>
#include <algorithm>
#include <math.h>
#include <time.h>
#include <set>
#include <map>
#include <queue>#define IOS     ios::sync_with_stdio(0);cin.tie(0);
#define rep(index,start,end) for(int index = start;index < end; index ++)
#define drep(index,start,end) for(int index = start;index >= end; index --)using namespace std;typedef long long ll;
ll gcd(ll a, ll b){ll t;while(b){t = b;b = a % b;a = t;}return a;
}const int maxn = 2e5+5;typedef pair<int, int> key;
int n,x,y;
map<key, int> store;
int main() {IOSint t;cin>>t;while(t--) {store.clear();cin>>n>>x>>y;int tmp;ll sum = 0LL;rep(i,0,n) {cin>>tmp;int modx = tmp % x;int mody = tmp % y;key now ={modx, mody};// calint bmody = tmp % y;int bmodx = (x - tmp%x) % x;sum += store[{bmodx, bmody}];if (store.find(now) != store.end()) {store[now] += 1;} else {store[now] = 1;}}cout<<sum<<endl;}return 0;
}

---

E. Anna and the Valentine’s Day Gift 博弈论

俩人玩游戏，一个能选一个数reverse，一个能选一个数拼接，看最后的结果能不能大于$10^m$

如果想要减少最终结果的位数，那么必须reverse之后产生前导零，例如10000，反转后变成1。那么这道题就变成了对反转后产生前导零个数的排序。注意我们的对手不傻，当我们把产生最多前导零的数字反转后，对手肯定会把产生第二多的拼接保护，防止最终结果位数减少，所以只能减去排序结果的偶数位

#include <iostream>
#include <string.h>
#include <algorithm>
#include <math.h>
#include <time.h>
#include <set>
#include <map>
#include <queue>#define IOS     ios::sync_with_stdio(0);cin.tie(0);
#define rep(index,start,end) for(int index = start;index < end; index ++)
#define drep(index,start,end) for(int index = start;index >= end; index --)using namespace std;typedef long long ll;
ll gcd(ll a, ll b){ll t;while(b){t = b;b = a % b;a = t;}return a;
}const int maxn = 2e5+5;struct node{int digit;int zero;
};int n,m;
node store[maxn];
bool cmp(const node& a, const node& b) {return a.zero > b.zero;
}
int main() {IOSint t;cin>>t;while(t--) {int tmp;cin>>n>>m;int sum = 0;rep(i,0,n) {cin>>tmp;int dig = 0;int zero = 0;bool leading = true;while(tmp > 0) {dig ++;if (leading && !(tmp % 10)) {zero ++;} else {leading = false;}tmp /= 10;}
//            cout<<"dig :"<<dig<<" zero:"<<zero<<endl;store[i].digit = dig;store[i].zero = zero;sum += dig;}sort(store, store+n, cmp);
//        cout<<"test log:"<<store[0].zero<<endl;for(int i=0;i<n;i+=2) {sum -= store[i].zero;}if (sum < m+1) {cout<<"Anna"<<endl;} else {cout<<"Sasha"<<endl;}}return 0;
}

---

https://codeforces.com/contest/1931/problem/F 拓扑排序

给几个数组，第一位没有用，问有没有一个排列能满足这几个数组中元素的先后关系。

数组给出的顺序天然形成有向图。像$1\to 2$且$2\to 1$这种矛盾的顺序必然是不存在序列的，也就是说给出的关系不能有环。所以简单套一个拓扑排序就可以了

#include <iostream>
#include <string.h>
#include <algorithm>
#include <math.h>
#include <time.h>
#include <set>
#include <map>
#include <queue>#define IOS     ios::sync_with_stdio(0);cin.tie(0);
#define rep(index,start,end) for(int index = start;index < end; index ++)
#define drep(index,start,end) for(int index = start;index >= end; index --)using namespace std;const int maxn = 2e5+5;int store[maxn];
vector<int> adj[maxn];
int in_degrad[maxn];
queue<int> Q;
int main() {IOSint t;cin>>t;while(t--) {int n,k;cin>>n>>k;// initmemset(in_degrad, 0, sizeof(in_degrad));rep(i,0,n+1) adj[i].clear();while(!Q.empty()) Q.pop();rep(i,0,k) {rep(j,0,n) cin>>store[j];rep(j,1,n-1) {int commonA = store[j];int commonB = store[j+1];if (find(adj[commonA].begin(), adj[commonA].end(), commonB) == adj[commonA].end()) {adj[commonA].push_back(commonB);in_degrad[commonB] ++;}}}rep(i,1,n+1) {if (!in_degrad[i])Q.push(i);}while (!Q.empty()) {int now = Q.front();Q.pop();int len = adj[now].size();rep(i,0,len) {int next = adj[now][i];if (-- in_degrad[next] == 0)Q.push(next);}}bool _loop = false;rep(i,1,n+1)if (in_degrad[i]) {
//                cout<<i<<' '<<in_degrad[i]<<endl;_loop = true;break;}cout<<(_loop? "NO":"YES")<<endl;}return 0;
}

---

G. One-Dimensional Puzzle 高二排列组合问题

题干太长懒得翻译 有多少种排列方式可以把给出的所有形状拼成一个长条。

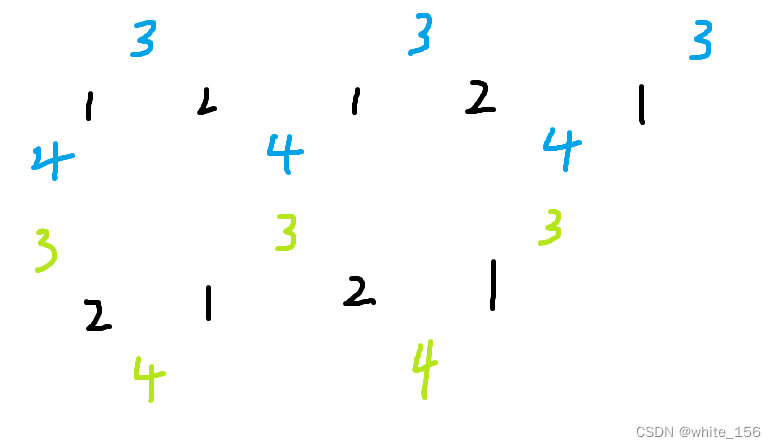
大概就是这么个拼接的方法。shape 1和shape 2的个数相差不能超过1，超过就拼不出来；shape 3和shape 4就是造成不同拼接方式的关键，穿插在shape 1和shape 2的间隙，要注意shape 3是可以自拼接，并不是每个间隙只能塞一个

#include <iostream>
#include <string.h>
#include <algorithm>
#include <math.h>
#include <time.h>
#include <set>
#include <map>
#include <queue>#define IOS     ios::sync_with_stdio(0);cin.tie(0);
#define mem(A,B) memset(A,B,sizeof(A));
#define rep(index,start,end) for(int index = start;index < end; index ++)
#define drep(index,start,end) for(int index = start;index >= end; index --)using namespace std;typedef long long ll;const int maxn = 3e6+5;
const int mod = 998244353;ll fact[maxn];ll pow_mod(ll x, ll p) {if (p == 0) {return 1;}if (p % 2 == 0) {ll y = pow_mod(x, p / 2);return (y * y) % mod;}return (x * pow_mod(x, p - 1)) % mod;
}ll inv(ll x) {return pow_mod(x, mod - 2);
}
ll cnk(ll n, ll k) {ll res = fact[n];res = (res * inv(fact[k])) % mod;res = (res * inv(fact[n - k])) % mod;
//    cout<<"n:"<<n<<" k:"<<k<<" res:"<<res<<endl;return res;
}
int abs(int num) {return num<0 ? -num :num;
}int store[5];
int main() {IOSfact[0] = fact[1] = 1;rep(i,2,maxn)fact[i] = (fact[i-1] * i) % mod;int t;cin>>t;while(t--) {rep(i,0,4) cin>>store[i];if (store[0] == 0 && store[1] == 0) {cout<<((store[2]!=0 && store[3] != 0)? 0:1)<<endl;continue;}int dfi = abs(store[1] - store[0]);if (dfi > 1) {cout<<0<<endl;continue;}ll ans = 0;if (dfi == 0) {// same and not 0int x3,x4;x3 = store[1];x4 = x3 + 1;ans += (cnk(store[2]+x3-1, store[2]) * cnk(store[3]+x4-1, store[3])) % mod;x4 = store[1];x3 = x4 + 1;ans = ans + (cnk(store[2]+x3-1, store[2]) * cnk(store[3]+x4-1, store[3])) % mod;ans = ans % mod;} else {// greater than oneint x3,x4;x3 = x4 = max(store[0], store[1]);ans = (cnk(store[2]+x3-1, store[2]) * cnk(store[3]+x4-1, store[3])) % mod;}cout<<ans<<endl;}return 0;
}