个人主页 ： zxctscl
如有转载请先通知

1. 14. 最长公共前缀

1.1 分析

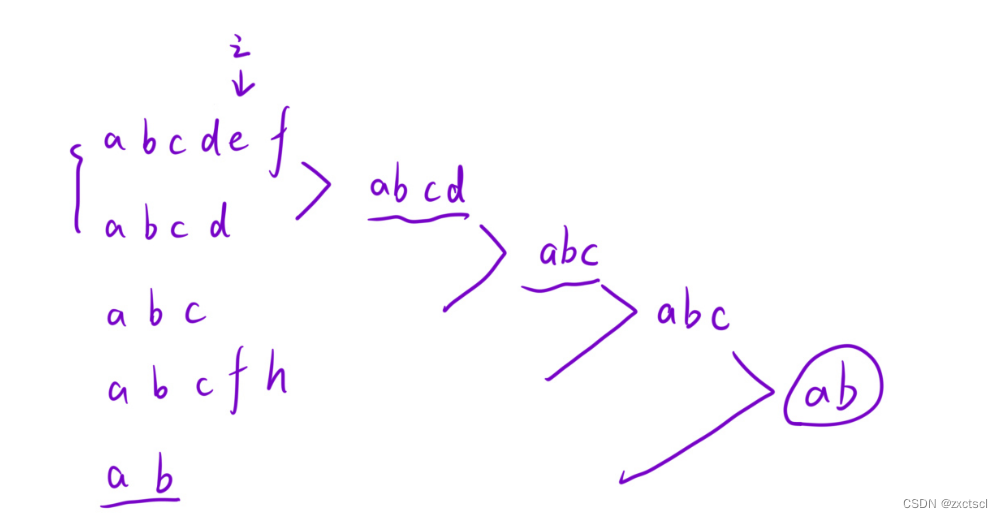
从第一个字符串开始两两比较，把比较相同的字符部分更新到一个存放目前相同字符的ret中，然后把ret继续向后面的字符串比较，继续更新ret就行。得注意一下，如果在比较中长度超过了那两个字符中叫小的一个，那么就这组比较就结束，换下一组来继续比较。

1.2 代码

class Solution {
public:string longestCommonPrefix(vector<string>& strs) {string ret=strs[0];for(int i=1;i<strs.size();i++){int j=0;while(j<min(ret.size(),strs[i].size())&&ret[j]==strs[i][j])j++;ret= ret.substr(0,j);}return ret;}    };

2. 5. 最长回文子串

2.1 分析

回文串有个特点，就是从中间扩展它的两边是对称的。
利用中心扩展算法，固定完中间位置后，用两个指针一个在走左边，一个走右边，如果两个指针执行的字符是一样的，就移动，一直到指针指向的字符不同，或者一个指针越界。
但是这里得分两种情况，如果回文串为奇数，这个方法是正确的；但是如果为偶数，把右边的中间位置加1，此时左右指针在同时移动的时候才是正确的。

总之就是，先固定一个中心点，然后从中心点开始向两边扩展，注意奇数长度以及偶数长度都需要考虑。

题目要的是最长回文子串，比较一下长度之后，更新一下最大的长度。

2.2 代码

class Solution {
public:string longestPalindrome(string s) {int begin=0,len=0,n=s.size();for(int i=0;i<n;i++){int left=i,right=i;//奇数while(left>=0&&right<n&&s[left]==s[right]){left--;right++;}if(right-left-1>len){begin=left+1;len=right-left-1;}left=i,right=i+1;//偶数while(left>=0&&right<n&&s[left]==s[right]){left--;right++;}if(right-left-1>len){begin=left+1;len=right-left-1;}}return s.substr(begin,len);}
};

3. 67. 二进制求和

3.1 分析

模拟的竖式计算的步骤，如果相加等于2，那么就进1，然后将这个字符取模就加到要返回的结果中，一直到两个字符串都结束。但是结果是与题目要的是相反的，所以得将得到字符串逆置。

3.2 代码

class Solution {
public:string addBinary(string a, string b) {string ret;int t=0;int cur1=a.size()-1,cur2=b.size()-1;while(cur1>=0||cur2>=0||t){if(cur1>=0) t+=a[cur1--]-'0';if(cur2>=0)t+=b[cur2--]-'0';ret+=t%2+'0';t/=2;}reverse(ret.begin(),ret.end());return ret;}
};

4. 43. 字符串相乘

4.1 分析

如果直接按照竖式计算来的话，思路是很简单的，但是代码不容易写，得处理进位和高位相乘要补上0，还得处理前导0和计算顺序，很多细节。
所以可以换一种方式，采用无进位相加。
把每一个位置的值相乘之后，先不进位，把每次计算的结果放在一个数组里面，最后再来处理进位。

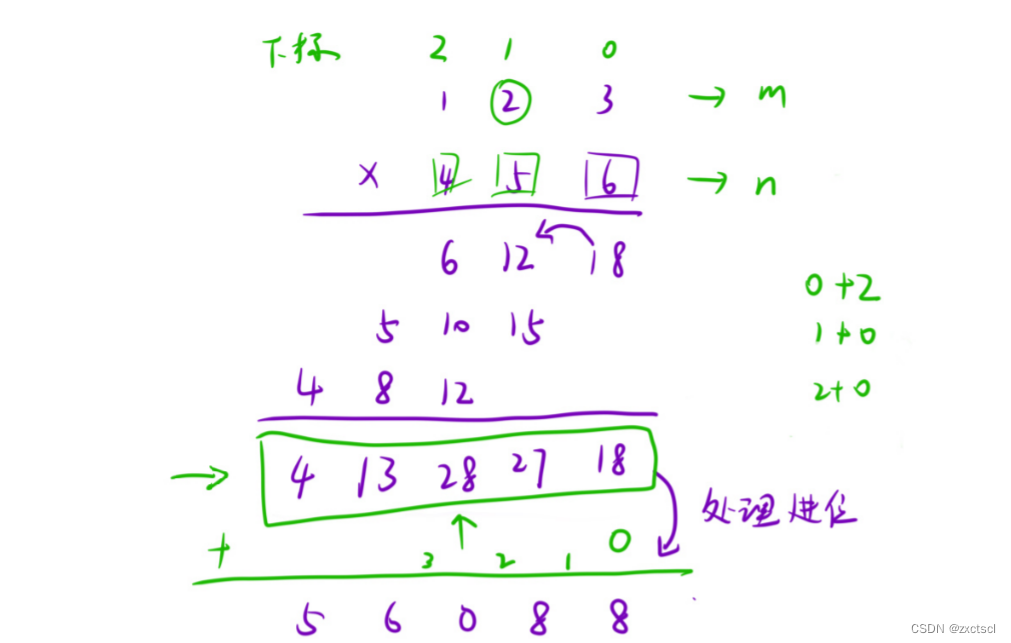
这里得先把两个字符串逆置,再无进位相乘相加，然后处理进位，最后处理前导0。

4.2 代码

class Solution {
public:string multiply(string num1, string num2) {int m=num1.size(),n=num2.size();reverse(num1.begin(),num1.end());reverse(num2.begin(),num2.end());vector<int> tmp(m+n-1);//无进位相乘相加for(int i=0;i<m;i++){for(int j=0;j<n;j++){tmp[i+j]+=(num1[i]-'0')*(num2[j]-'0');}}//处理进位int cur=0,t=0;string ret;while(cur<m+n-1||t!=0){if(cur<m+n-1)t+=tmp[cur++];ret+=t%10+'0';t/=10;}//处理前导0while(ret.size()>1&&ret.back()=='0')ret.pop_back();reverse(ret.begin(),ret.end());return ret;}
};

有问题请指出，大家一起进步！！！