节点的度：该节点拥有的孩子个数

叶子节点：度为0的节点

层数：根节点为第一层，根的子节点为第二层，以此类推

所有树的性质：所有节点的总度数等于节点数减一

完全m叉树性质

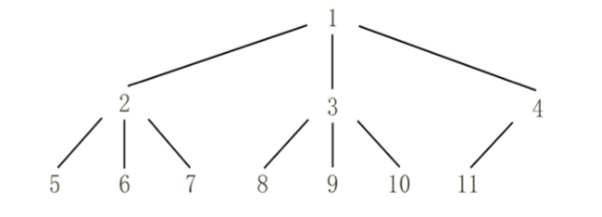
完全m 叉树，节点的度数最大为m ，且必须按照从上到下从左到右的顺序依次填满，叶子节点只出现在倒数第一层和倒数第二层，如以下为一个完全三叉树

(1)第i 层最多拥有的节点个数为

(2)d 层的完全m 叉树最多拥有的节点个数为

假设完全m 叉树有n 个节点

(3) n 个结点的完全m 叉树的深度为 , ceil 表示向上取整

(4) 当i<d 时，第i 层节点个数为

第d 层的节点个数为

(5)在满m 叉树中，一个编号为p 的结点(编号从1开始)，它的深度是 ，它的父节点编号为 ，易得该结点的第k-1 个孩子的编号为p*k ，所以推导出该结点的第i 个孩子的编号为  

(6)对于n 个结点的二叉树，按从上到下，从左到右依次给结点编号

i 的双亲结点为i//2 ，若n<2i ，则i 是叶子结点，若n≥2i ，则其左孩子为2i ，若n≥2i+1 ，则其右孩子是结点2i+1 ,若n<2i+1 ，则其无左孩子

(7) n 个结点的不同二叉树有 种

经典例题

已知一个二叉树有x0 个叶子结点，则该二叉树的总结点数至少是

需要最少的结点，则除了叶子结点外其它结点度数都为2，设度数为2的结点有x2 个，则根据度数性质：所有节点的总度数等于节点数减一

所以该二叉树的总结点数至少是