论文笔记：The Expressive Power of Transformers with Chain of Thought

ICLR 2024 reviewer 评分 6888【但是chair 很不喜欢】

1 intro

之前的研究表明，即使是具有理想参数的标准Transformer，也无法完美解决许多大规模的顺序推理问题，如模拟有限状态机、判断图中的节点是否相连，或解决矩阵等式问题
- 这里的直觉是，Transformer缺乏递归连接，而解决这些顺序推理问题需要递归
- 实证上，受这些结果启发的推理问题无法被最先进的变压器语言模型如ChatGPT和GPT-4所解决，且GPT-4的推理性能与问题的计算图深度负相关
- ——>结果表明某些类型的顺序推理对变压器构成挑战，并激励了解决这一问题的扩展
一种在提升Transformer顺序推理方面已经实证成功的方法是增加所谓的思考链（CoT）或草稿本
- 这些方法允许Transformer在回答前输出一系列中间令牌，而不是在读入输入后立即回答
- 直观上，这种方法可以在顺序推理问题上解锁更大的表现力，因为模型可以将每个中间令牌作为一种递归状态使用
论文描述在生成答案前采取中间步骤的Transformer解码器的推理能力，并将其与没有中间步骤的Transformer进行比较
- 提供了Transformer能力的上限和下限，取决于t(n)：允许的中间步骤数量作为输入大小n的函数。
  - 主要关注三种情况：
    - 对数步骤（当t(n) = Θ(log n)）
    - 线性步骤（当t(n) = Θ(n)）
    - 和多项式步骤
无中间步骤
- 没有任何中间步骤的Transformer解码器只能解决属于相当小的电路复杂度类和相关逻辑类的问题
  - ——>基本的Transformer远非图灵完备：它们甚至无法解决比 $TC^0$ 更大的类的完备问题，如模拟自动机（NC1-完备）、决定有向图连通性（NL-完备）或解决线性等式（P-完备）
对数步骤
- 通过对数数量的中间步骤，我们展示了Transformer的上界从TC0略微扩展到L
- ——>这意味着具有对数数量中间步骤的Transformer可能获得了一些能力，但它们仍然无法解决像有向图连通性这样的NL-完备问题或解决线性等式这样的P-完备问题
线性步骤
- 线性中间步骤允许具有预投影范数的Transformer模拟自动机（NC1-完备）
  - 如果没有中间步骤（除非TC0等于NC1），否则无法完成这一任务
多项式步骤
- 通过多项式数量的解码步骤，论文展示了具有严格因果注意力和预投影范数的Transformer等同于P类。
- 据我们所知，这是Transformer类与标准复杂度类之间的首次等价。

2 主要结论

2.1 具有中间解码的Transformer的能力

TIME(t(n)) 为存在一个在时间 O(t(n)) 内运行并接受语言 L 的图灵机的语言类
为在中的问题类
- 对于某些 k，这是当 t(n) ≥ n 时有意义的
SPACE(s(n)) 为存在一个带宽受 O(s(n)) 限制的图灵机接受语言 L 的语言类
CoT(t(n)) 表示一些使用 t(n) 解码步骤的变压器识别的语言集

——>具有 t(n) 步骤的Transformer与标准时间/空间复杂性类之间的以下关系

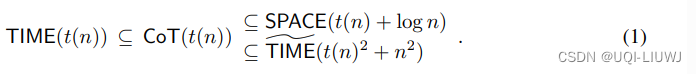
2.2 具有思考链的Transformer的能力

方程（1）的左侧表明，具有 Θ(n) 步骤的Transformer解码器可以模拟如自动机或计数机这类的实时计算模型
- 在复杂性理论的标准假设下，没有解码步骤的Transformer无法模拟所有自动机
- ——>线性数量的解码步骤显著增强了变压器的能力
同样，方程（1）的左侧意味着具有二次数量步骤的Transformer可以实现线性时间算法（用于随机访问图灵机）来解决有向图连通性问题，这是一个超出标准Transformer能力范围的问题
具有多项式数量解码步骤的变压器可以解决线性等式、霍恩子句满足性和通用上下文无关识别问题，这些都是 P-完备问题，标准变压器已知无法表达

2.3 具有思考链的Transformer的局限性

方程（1）的右侧确定了依赖于 t(n) 和 n 的变压器解码器中间步骤的两个上界。
论文探讨了这一总结果在不同 t(n) 情形下的含义：
- 对数步骤：具有 O(log n) 中间步骤的变压器解码器只能识别 L = SPACE(log n) 中的语言
  - ——>具有 O(log n) 中间步骤的变压器无法解决如有向图连通性这样的 NL-或 P-完备问题，就像没有中间解码步骤的变压器一样
- 线性步骤：具有 O(n) 中间步骤的变压器解码器只能识别同时位于和 SPACE(n) 中的语言
  - 由于 SPACE(n) 属于上下文敏感语言——>具有线性步骤的变压器最多可以识别上下文敏感语言
  - 结合我们的下界，这表明具有 Θ(n) 步骤的变压器解码器在乔姆斯基层级结构中处于正则语言和上下文敏感语言之间
- 多项式步骤：
  - 如果 t(n) = O(n^c) 对于某些 c，我们得到的上限是 $P= \bigcup_0^\infty TIME(n^c)$
  - 结合我们的下界，这表明具有多项式数量步骤的变压器解码器精确地识别 P 类问题
  - ——>多项式数量的步骤将Transformer转化为强大的推理器，尽管在实践中使用大型Transformer运行多项式数量的前向传递可能是不切实际的