实验8:分类与预测建模
一:实验目的与要求
1:学习和掌握回归分析、决策树、人工神经网络、KNN算法、朴素贝叶斯分类等机器学习算法在R语言中的应用。
2:了解其他分类与预测算法函数。
3:学习和掌握分类与预测算法的评价。
二:实验内容
【回归分析】
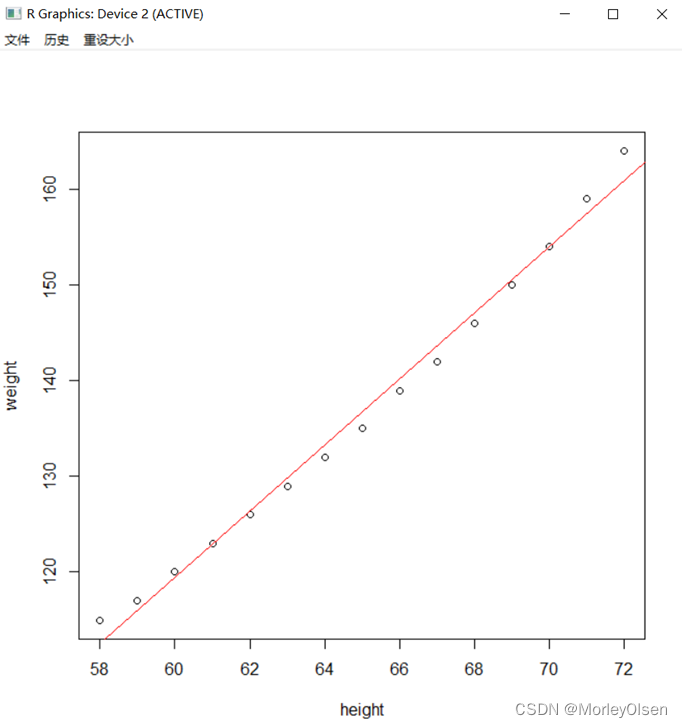
Eg.1:
| attach(women) fit<-lm(weight ~ height) plot(height,weight) abline(fit,col="red") detach(women) |
【线性回归模型】
Eg.1:利用数据集women建立简单线性回归模型
| data(women) lm.model <- lm( weight ~ height - 1, data = women) # 建立线性回归模型 summary(lm.model) # 输出模型的统计信息 coefficients(lm.model) # 输出参数估计值 confint(lm.model, parm = "speed", level = 0.95) # parm缺省则计算所有参数的置信区间 fitted(lm.model) # 列出拟合模型的预测值 anova(lm.model) # 生成一个拟合模型的方差分析表 vcov(lm.model) # 列出模型参数的协方差矩阵 residuals(lm.model) # 列出模型的残差 AIC(lm.model) # 输出AIC值 par(mfrow = c(2, 2)) plot(lm.model) # 生成评价拟合模型的诊断图 |




【逻辑回归模型】
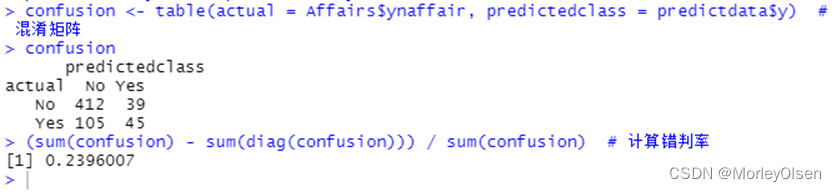
Eg.1:结婚时间、教育、宗教等其它变量对出轨次数的影响
| install.packages("AER") library(AER) data(Affairs, package = "AER") # 由于变量affairs为正整数,为了进行Logistic回归先要将其转化为二元变量。 Affairs$ynaffair[Affairs$affairs > 0] <- 1 Affairs$ynaffair[Affairs$affairs == 0] <- 0 Affairs$ynaffair <- factor(Affairs$ynaffair, levels = c(0, 1), labels = c("No", "Yes")) # 建立Logistic回归模型 model.L <- glm(ynaffair ~ age + yearsmarried + religiousness + rating, data = Affairs, family = binomial (link = logit)) summary(model.L) # 展示拟合模型的详细结果 predictdata <- data.frame(Affairs[, c("age", "yearsmarried", "religiousness", "rating")]) # 由于拟合结果是给每个观测值一个概率值,下面以0.4作为分类界限 predictdata$y <- (predict(model.L, predictdata, type = "response") > 0.4) predictdata$y[which(predictdata$y == FALSE)] = "No" # 把预测结果转换成原先的值(Yes或No) predictdata$y[which(predictdata$y == TRUE)] = "Yes" confusion <- table(actual = Affairs$ynaffair, predictedclass = predictdata$y) # 混淆矩阵 confusion (sum(confusion) - sum(diag(confusion))) / sum(confusion) # 计算错判率 |


【Bonferroni离群点检验】
Eg.1:对美国妇女的平均身高和体重数据进行Bonferroni离群点检验
| install.packages("car") library(car) fit <- lm(weight ~ height, data = women) # 建立线性模型 outlierTest(fit) # Bonferroni离群点检验 women[10, ] <- c(70, 200) # 将第10个观测的数据该成height = 70,weight = 200 fit <- lm(weight ~ height, data = women) outlierTest(fit) # Bonferroni离群点检验 |

【检验误差项的自相关性】
Eg.1:对模型lm.model的误差做自相关性检验
| durbinWatsonTest(lm.model) |

【自变量选择】
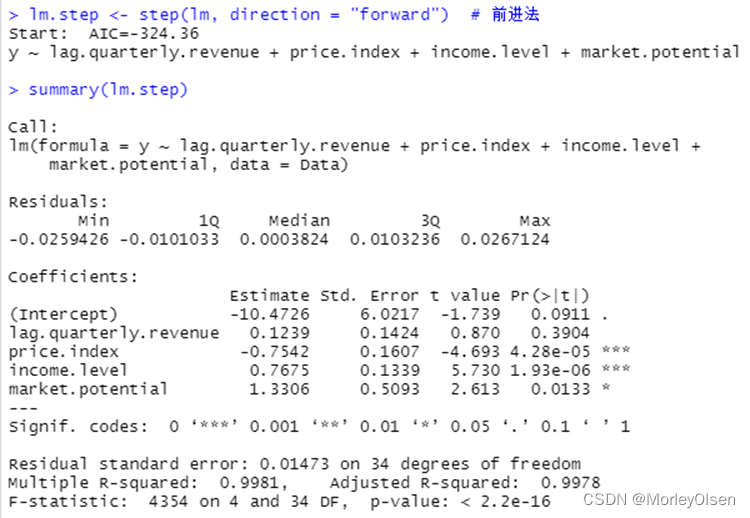
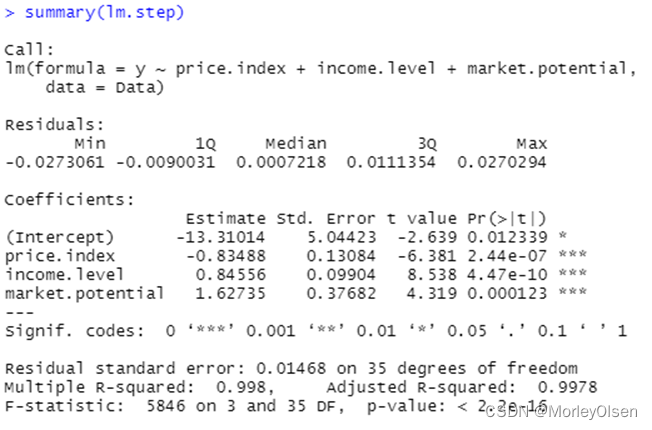
Eg.1:使用数据集freeny建立逻辑回归模型,并进行自变量选择
| Data <- freeny lm <- lm(y ~ ., data = Data) # logistic回归模型 summary(lm) lm.step <- step(lm, direction = "both") # 一切子集回归 summary(lm.step) lm.step <- step(lm, direction = "forward") # 前进法 summary(lm.step) lm.step <- step(lm, direction = "backward") # 后退法 summary(lm.step) |




【C4.5决策树】
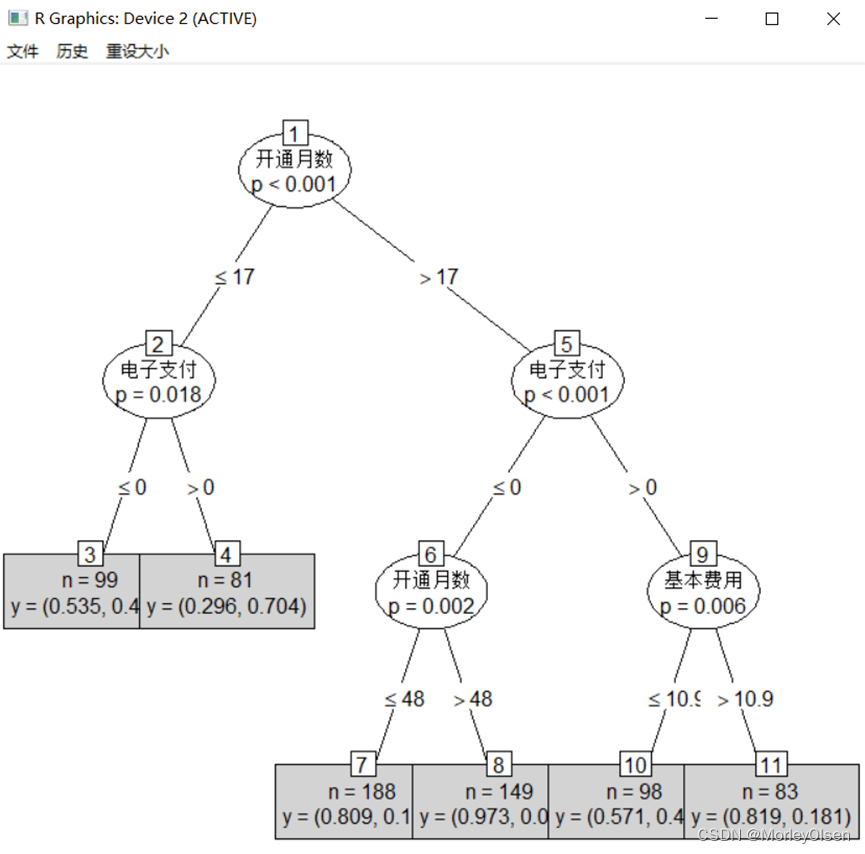
Eg.1:C4.5决策树预测客户是否流失
| Data <- read.csv("Telephone.csv",fileEncoding = "GB2312") # 读入数据 Data[, "流失"] <- as.factor(Data[, "流失"]) # 将目标变量转换成因子型 set.seed(1234) # 设置随机种子 # 数据集随机抽70%定义为训练数据集,30%为测试数据集 ind <- sample(2, nrow(Data), replace = TRUE, prob = c(0.7, 0.3)) traindata <- Data[ind == 1, ] testdata <- Data[ind == 2, ] # 建立决策树模型预测客户是否流失 install.packages("matrixStats") install.packages("party") library(party) # 加载决策树的包 ctree.model <- ctree(流失 ~ ., data = traindata) # 建立C4.5决策树模型 plot(ctree.model, type = "simple") # 输出决策树图 # 预测结果 train_predict <- predict(ctree.model) # 训练数据集 test_predict <- predict(ctree.model, newdata = testdata) # 测试数据集 # 输出训练数据的分类结果 # 输出训练数据的分类结果 train_predictdata <- cbind(traindata, predictedclass = train_predict) #输出训练数据的混淆矩阵 (train_confusion <- table(actual = traindata$流失, predictedclass = train_predict) ) # 输出测试数据的分类结果 test_predictdata <- cbind(testdata, predictedclass = test_predict) # 输出测试数据的混淆矩阵 (test_confusion <- table(actual = testdata$流失, predictedclass = test_predict)) |

【CART决策树】
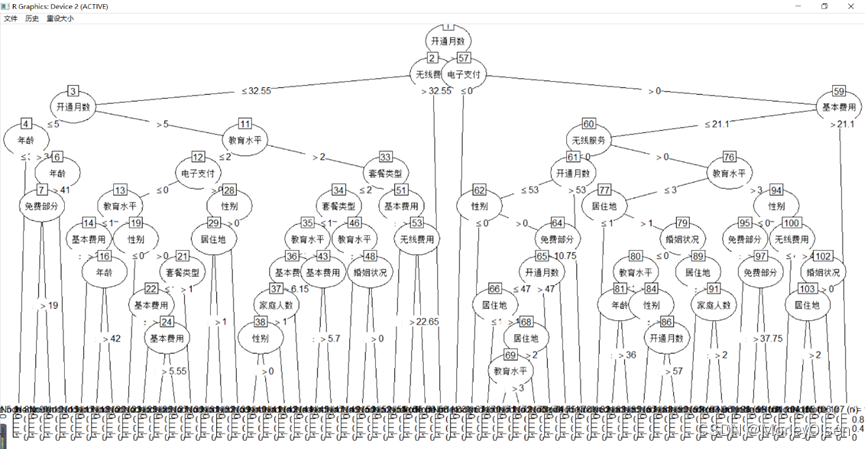
Eg.1:CART决策树预测客户是否流失
| Data <- read.csv("telephone.csv",fileEncoding = "GB2312") # 读入数据 Data[, "流失"] <- as.factor(Data[, "流失"]) # 将目标变量转换成因子型 set.seed(1234) # 设置随机种子 # 数据集随机抽70%定义为训练数据集,30%为测试数据集 ind <- sample(2, nrow(Data), replace = TRUE, prob = c(0.7, 0.3)) traindata <- Data[ind == 1, ] testdata <- Data[ind == 2, ] # 建立决策树模型预测客户是否流失 install.packages("tree") library(tree) # 加载决策树的包 tree.model <- tree(流失 ~ ., data = traindata) # 建立CART决策树模型 plot(tree.model, type = "uniform") # 输出决策树图 text(tree.model) # 预测结果 train_predict <- predict(tree.model, type = "class") # 训练数据集 test_predict <- predict(tree.model, newdata = testdata, type = "class") # 测试数据集 # 输出训练数据的分类结果 train_predictdata <- cbind(traindata, predictedclass = train_predict) # 输出训练数据的混淆矩阵 (train_confusion <- table(actual = traindata$流失, predictedclass = train_predict)) # 输出测试数据的分类结果 test_predictdata <- cbind(testdata, predictedclass = test_predict) # 输出测试数据的混淆矩阵 (test_confusion <- table(actual = testdata$流失, predictedclass = test_predict)) |


【C5.0决策树】
Eg.1:C5.0决策树预测客户是否流失
| Data <- read.csv("telephone.csv",fileEncoding = "GB2312") # 读入数据 Data[, "流失"] <- as.factor(Data[, "流失"]) # 将目标变量转换成因子型 set.seed(1234) # 设置随机种子 # 数据集随机抽70%定义为训练数据集,30%为测试数据集 ind <- sample(2, nrow(Data), replace = TRUE, prob = c(0.7, 0.3)) traindata <- Data[ind == 1, ] testdata <- Data[ind == 2, ] # 建立决策树模型预测客户是否流失 install.packages("C50") library(C50) # 加载决策树的包 c50.model <- C5.0(流失 ~ ., data = traindata) # 建立C5.0决策树模型 plot(c50.model) # 输出决策树图 # 预测结果 train_predict <- predict(c50.model, newdata = traindata, type = "class") # 训练数据集 test_predict <- predict(c50.model, newdata = testdata, type = "class") # 测试数据集 # 输出训练数据的分类结果 train_predictdata <- cbind(traindata, predictedclass = train_predict) # 输出训练数据的混淆矩阵 (train_confusion <- table(actual = traindata$流失, predictedclass = train_predict)) # 输出测试数据的分类结果 test_predictdata <- cbind(testdata, predictedclass = test_predict) # 输出测试数据的混淆矩阵 (test_confusion <- table(actual = testdata$流失, predictedclass = test_predict)) |

【BP神经网络】
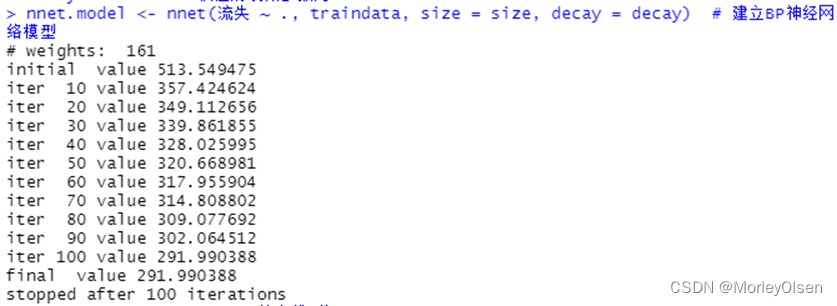
Eg.1:BP神经网络算法预测客户是否流失
| Data[, "流失"] <- as.factor(Data[, "流失"]) # 将目标变量转换成因子型 set.seed(1234) # 设置随机种子 # 数据集随机抽70%定义为训练数据集,30%为测试数据集 ind <- sample(2, nrow(Data), replace = TRUE, prob = c(0.7, 0.3)) traindata <- Data[ind == 1, ] testdata <- Data[ind == 2, ] # BP神经网络建模 library(nnet) #加载nnet包 # 设置参数 size <- 10 # 隐层节点数为10 decay <- 0.05 # 权值的衰减参数为0.05 nnet.model <- nnet(流失 ~ ., traindata, size = size, decay = decay) # 建立BP神经网络模型 summary(nnet.model) # 输出模型概要 # 预测结果 train_predict <- predict(nnet.model, newdata = traindata, type = "class") # 训练数据集 test_predict <- predict(nnet.model, newdata = testdata, type = "class") # 测试数据集 # 输出训练数据的分类结果 train_predictdata <- cbind(traindata, predictedclass = train_predict) # 输出训练数据的混淆矩阵 (train_confusion <- table(actual = traindata$流失, predictedclass = train_predict)) # 输出测试数据的分类结果 test_predictdata <- cbind(testdata, predictedclass = test_predict) # 输出测试数据的混淆矩阵 (test_confusion <- table(actual = testdata$流失, predictedclass = test_predict)) |



【KNN算法】
Eg.1:KNN算法预测客户是否流失
| Data[, "流失"] <- as.factor(Data[, "流失"]) # 将目标变量转换成因子型 set.seed(1234) # 设置随机种子 # 数据集随机抽70%定义为训练数据集,30%为测试数据集 ind <- sample(2, nrow(Data), replace = TRUE, prob = c(0.7, 0.3)) traindata <- Data[ind == 1, ] testdata <- Data[ind == 2, ] # 使用kknn函数建立knn分类模型 install.packages("kknn") library(kknn) # 加载kknn包 # knn分类模型 kknn.model <- kknn(流失 ~ ., train = traindata, test = traindata, k = 5) # 训练数据 kknn.model2 <- kknn(流失 ~ ., train = traindata, test = testdata, k = 5) # 测试数据 summary(kknn.model) # 输出模型概要 # 预测结果 train_predict <- predict(kknn.model) # 训练数据 test_predict <- predict(kknn.model2) # 测试数据 # 输出训练数据的混淆矩阵 (train_confusion <- table(actual = traindata$流失, predictedclass = train_predict)) # 输出测试数据的混淆矩阵 (test_confusion <- table(actual = testdata$流失, predictedclass = test_predict)) # 使用knn函数建立knn分类模型 library(class) # 加载class包 # 建立knn分类模型 knn.model <- knn(traindata, testdata, cl = traindata[, "流失"]) # 输出测试数据的混淆矩阵 (test_confusion = table(actual = testdata$流失, predictedclass = knn.model)) # 使用train函数建立knn分类模型 install.packages("caret") library(caret) # 加载caret包 # 建立knn分类模型 train.model <- train(traindata, traindata[, "流失"], method = "knn") # 预测结果 train_predict <- predict(train.model, newdata = traindata) #训练数据集 test_predict <- predict(train.model, newdata = testdata) #测试数据集 # 输出训练数据的混淆矩阵 (train_confusion <- table(actual = traindata$流失, predictedclass = train_predict)) # 输出测试数据的混淆矩阵 (test_confusion <- table(actual = testdata$流失, predictedclass = test_predict)) |
运行结果:
| 模型概要输出 |
| Call: kknn(formula = 流失 ~ ., train = traindata, test = traindata, k = 5) Response: "nominal" fit prob.0 prob.1 1 1 0.33609798 0.66390202 2 1 0.25597771 0.74402229 3 0 0.97569952 0.02430048 4 0 0.51243637 0.48756363 5 0 1.00000000 0.00000000 6 1 0.17633839 0.82366161 7 0 0.59198438 0.40801562 8 0 1.00000000 0.00000000 9 0 1.00000000 0.00000000 10 1 0.36039846 0.63960154 11 0 0.74402229 0.25597771 12 0 0.84796209 0.15203791 13 0 0.89557925 0.10442075 14 0 1.00000000 0.00000000 15 0 1.00000000 0.00000000 16 0 0.74402229 0.25597771 17 1 0.02430048 0.97569952 18 1 0.15203791 0.84796209 19 0 1.00000000 0.00000000 20 0 0.97569952 0.02430048 21 0 0.97569952 0.02430048 22 0 1.00000000 0.00000000 23 0 0.76784183 0.23215817 24 0 0.74354135 0.25645865 25 0 0.74402229 0.25597771 26 0 1.00000000 0.00000000 27 0 1.00000000 0.00000000 28 0 0.51186411 0.48813589 29 0 1.00000000 0.00000000 30 0 0.97569952 0.02430048 31 0 1.00000000 0.00000000 32 0 0.56768390 0.43231610 33 0 0.84796209 0.15203791 34 0 0.66390202 0.33609798 35 1 0.00000000 1.00000000 36 0 1.00000000 0.00000000 37 0 1.00000000 0.00000000 38 0 0.84796209 0.15203791 39 1 0.25597771 0.74402229 40 1 0.48813589 0.51186411 41 1 0.36039846 0.63960154 42 0 0.97569952 0.02430048 43 0 0.89557925 0.10442075 44 0 1.00000000 0.00000000 45 0 0.51243637 0.48756363 46 0 0.66390202 0.33609798 47 0 0.74402229 0.25597771 48 0 1.00000000 0.00000000 49 0 1.00000000 0.00000000 50 0 1.00000000 0.00000000 51 1 0.36039846 0.63960154 52 0 0.91987973 0.08012027 53 0 1.00000000 0.00000000 54 0 0.91987973 0.08012027 55 1 0.25597771 0.74402229 56 0 0.89557925 0.10442075 57 0 0.91987973 0.08012027 58 0 1.00000000 0.00000000 59 0 0.56768390 0.43231610 60 1 0.48813589 0.51186411 61 0 1.00000000 0.00000000 62 0 1.00000000 0.00000000 63 1 0.48756363 0.51243637 64 0 0.51243637 0.48756363 65 0 0.51243637 0.48756363 66 0 0.84796209 0.15203791 67 0 0.84796209 0.15203791 68 0 0.76784183 0.23215817 69 1 0.02430048 0.97569952 70 1 0.00000000 1.00000000 71 0 0.84796209 0.15203791 72 0 0.76784183 0.23215817 73 0 0.76784183 0.23215817 74 1 0.15203791 0.84796209 75 1 0.02430048 0.97569952 76 0 1.00000000 0.00000000 77 0 0.51243637 0.48756363 78 1 0.36039846 0.63960154 79 0 0.71972181 0.28027819 80 0 0.82366161 0.17633839 81 1 0.36039846 0.63960154 82 1 0.23215817 0.76784183 83 0 0.76784183 0.23215817 84 1 0.00000000 1.00000000 85 0 1.00000000 0.00000000 86 0 0.66390202 0.33609798 87 0 1.00000000 0.00000000 88 0 0.91987973 0.08012027 89 1 0.23215817 0.76784183 90 0 1.00000000 0.00000000 91 0 0.91987973 0.08012027 92 0 1.00000000 0.00000000 93 0 1.00000000 0.00000000 94 1 0.10442075 0.89557925 95 0 0.91987973 0.08012027 96 0 0.74354135 0.25645865 97 1 0.25645865 0.74354135 98 1 0.33609798 0.66390202 99 0 0.91987973 0.08012027 100 1 0.25645865 0.74354135 101 0 1.00000000 0.00000000 102 1 0.28027819 0.71972181 103 0 0.66390202 0.33609798 104 0 0.51186411 0.48813589 105 0 0.56768390 0.43231610 106 0 0.84796209 0.15203791 107 0 0.76784183 0.23215817 108 0 1.00000000 0.00000000 109 0 0.76784183 0.23215817 110 0 0.91987973 0.08012027 111 1 0.43231610 0.56768390 112 0 1.00000000 0.00000000 113 0 0.97569952 0.02430048 114 0 1.00000000 0.00000000 115 0 0.76784183 0.23215817 116 0 0.63960154 0.36039846 117 0 0.97569952 0.02430048 118 1 0.15203791 0.84796209 119 0 0.74402229 0.25597771 120 0 1.00000000 0.00000000 121 0 1.00000000 0.00000000 122 0 0.91987973 0.08012027 123 0 1.00000000 0.00000000 124 0 0.74354135 0.25645865 125 0 1.00000000 0.00000000 126 1 0.43231610 0.56768390 127 0 0.71972181 0.28027819 128 1 0.08012027 0.91987973 129 0 0.91987973 0.08012027 130 1 0.10442075 0.89557925 131 0 1.00000000 0.00000000 132 0 0.91987973 0.08012027 133 0 0.51243637 0.48756363 134 0 0.66390202 0.33609798 135 1 0.02430048 0.97569952 136 0 1.00000000 0.00000000 137 0 0.74354135 0.25645865 138 0 0.97569952 0.02430048 139 0 1.00000000 0.00000000 140 0 1.00000000 0.00000000 141 1 0.25597771 0.74402229 142 0 1.00000000 0.00000000 143 0 1.00000000 0.00000000 144 1 0.36039846 0.63960154 145 0 1.00000000 0.00000000 146 0 0.74402229 0.25597771 147 0 0.84796209 0.15203791 148 0 0.91987973 0.08012027 149 0 0.51243637 0.48756363 150 0 1.00000000 0.00000000 151 1 0.28027819 0.71972181 152 0 1.00000000 0.00000000 153 0 0.59198438 0.40801562 154 0 0.51243637 0.48756363 155 1 0.33609798 0.66390202 156 0 0.97569952 0.02430048 157 0 1.00000000 0.00000000 158 0 1.00000000 0.00000000 159 0 0.59198438 0.40801562 160 1 0.48756363 0.51243637 161 0 1.00000000 0.00000000 162 0 0.97569952 0.02430048 163 1 0.25645865 0.74354135 164 1 0.33609798 0.66390202 165 0 0.51186411 0.48813589 166 1 0.43231610 0.56768390 167 0 1.00000000 0.00000000 168 0 1.00000000 0.00000000 169 0 1.00000000 0.00000000 170 0 1.00000000 0.00000000 171 0 1.00000000 0.00000000 172 0 0.76784183 0.23215817 173 0 0.56768390 0.43231610 174 0 0.76784183 0.23215817 175 0 0.84796209 0.15203791 176 0 1.00000000 0.00000000 177 0 0.51243637 0.48756363 178 0 0.51243637 0.48756363 179 0 0.63960154 0.36039846 180 0 0.74402229 0.25597771 181 0 1.00000000 0.00000000 182 1 0.15203791 0.84796209 183 0 0.66390202 0.33609798 184 1 0.02430048 0.97569952 185 0 0.97569952 0.02430048 186 1 0.23215817 0.76784183 187 0 0.97569952 0.02430048 188 0 0.51186411 0.48813589 189 1 0.25597771 0.74402229 190 0 1.00000000 0.00000000 191 0 1.00000000 0.00000000 192 0 1.00000000 0.00000000 193 0 1.00000000 0.00000000 194 0 1.00000000 0.00000000 195 0 0.91987973 0.08012027 196 0 1.00000000 0.00000000 197 0 0.91987973 0.08012027 198 0 0.74402229 0.25597771 199 0 1.00000000 0.00000000 200 0 1.00000000 0.00000000 201 0 1.00000000 0.00000000 202 0 1.00000000 0.00000000 203 0 0.97569952 0.02430048 204 0 0.84796209 0.15203791 205 1 0.00000000 1.00000000 206 0 0.89557925 0.10442075 207 0 1.00000000 0.00000000 208 0 1.00000000 0.00000000 209 0 0.91987973 0.08012027 210 0 0.84796209 0.15203791 211 0 1.00000000 0.00000000 212 0 0.74402229 0.25597771 213 0 0.74402229 0.25597771 214 0 0.66390202 0.33609798 215 0 1.00000000 0.00000000 216 0 0.91987973 0.08012027 217 0 1.00000000 0.00000000 218 0 1.00000000 0.00000000 219 0 0.51186411 0.48813589 220 0 1.00000000 0.00000000 221 1 0.00000000 1.00000000 222 1 0.15203791 0.84796209 223 0 0.51243637 0.48756363 224 1 0.28027819 0.71972181 225 1 0.08012027 0.91987973 226 0 1.00000000 0.00000000 227 0 1.00000000 0.00000000 228 1 0.25597771 0.74402229 229 1 0.15203791 0.84796209 230 1 0.15203791 0.84796209 231 0 0.51243637 0.48756363 232 1 0.08012027 0.91987973 233 1 0.28027819 0.71972181 234 1 0.40801562 0.59198438 235 0 0.51186411 0.48813589 236 0 1.00000000 0.00000000 237 1 0.43231610 0.56768390 238 0 0.89557925 0.10442075 239 1 0.33609798 0.66390202 240 0 0.74354135 0.25645865 241 0 0.97569952 0.02430048 242 0 1.00000000 0.00000000 243 0 0.97569952 0.02430048 244 0 0.89557925 0.10442075 245 0 0.74402229 0.25597771 246 0 1.00000000 0.00000000 247 0 1.00000000 0.00000000 248 0 0.84796209 0.15203791 249 1 0.36039846 0.63960154 250 0 0.84796209 0.15203791 251 1 0.48813589 0.51186411 252 0 1.00000000 0.00000000 253 0 1.00000000 0.00000000 254 0 0.91987973 0.08012027 255 0 0.56768390 0.43231610 256 0 1.00000000 0.00000000 257 0 0.84796209 0.15203791 258 1 0.33609798 0.66390202 259 0 0.76784183 0.23215817 260 0 1.00000000 0.00000000 261 1 0.36039846 0.63960154 262 0 1.00000000 0.00000000 263 0 1.00000000 0.00000000 264 1 0.48756363 0.51243637 265 1 0.48756363 0.51243637 266 0 0.89557925 0.10442075 267 0 1.00000000 0.00000000 268 0 0.66390202 0.33609798 269 0 0.56768390 0.43231610 270 0 0.74402229 0.25597771 271 1 0.25597771 0.74402229 272 0 1.00000000 0.00000000 273 0 0.66390202 0.33609798 274 0 1.00000000 0.00000000 275 0 1.00000000 0.00000000 276 0 0.89557925 0.10442075 277 0 1.00000000 0.00000000 278 0 0.51243637 0.48756363 279 0 0.84796209 0.15203791 280 0 1.00000000 0.00000000 281 0 0.84796209 0.15203791 282 0 0.91987973 0.08012027 283 0 1.00000000 0.00000000 284 0 1.00000000 0.00000000 285 0 0.97569952 0.02430048 286 0 1.00000000 0.00000000 287 0 1.00000000 0.00000000 288 0 1.00000000 0.00000000 289 0 1.00000000 0.00000000 290 0 0.91987973 0.08012027 291 0 1.00000000 0.00000000 292 0 1.00000000 0.00000000 293 0 0.91987973 0.08012027 294 0 0.76784183 0.23215817 295 1 0.17633839 0.82366161 296 1 0.10442075 0.89557925 297 0 0.84796209 0.15203791 298 0 0.97569952 0.02430048 299 1 0.36039846 0.63960154 300 0 1.00000000 0.00000000 301 0 0.84796209 0.15203791 302 0 0.91987973 0.08012027 303 0 0.89557925 0.10442075 304 0 0.97569952 0.02430048 305 0 1.00000000 0.00000000 306 1 0.02430048 0.97569952 307 1 0.15203791 0.84796209 308 1 0.40801562 0.59198438 309 0 0.84796209 0.15203791 310 1 0.00000000 1.00000000 311 0 0.89557925 0.10442075 312 0 1.00000000 0.00000000 313 0 1.00000000 0.00000000 314 1 0.48756363 0.51243637 315 0 0.51243637 0.48756363 316 0 0.97569952 0.02430048 317 0 1.00000000 0.00000000 318 0 0.97569952 0.02430048 319 1 0.25645865 0.74354135 320 0 1.00000000 0.00000000 321 1 0.08012027 0.91987973 322 1 0.33609798 0.66390202 323 0 0.91987973 0.08012027 324 0 0.89557925 0.10442075 325 0 0.91987973 0.08012027 326 0 1.00000000 0.00000000 327 1 0.25597771 0.74402229 328 0 1.00000000 0.00000000 329 0 1.00000000 0.00000000 330 1 0.43231610 0.56768390 331 0 0.84796209 0.15203791 332 0 0.51243637 0.48756363 333 1 0.33609798 0.66390202 [ reached 'max' / getOption("max.print") -- omitted 365 rows ] |


【朴素贝叶斯分类算法】
Eg.1:朴素贝叶斯算法预测客户是否流失
| Data[, "流失"] <- as.factor(Data[, "流失"]) # 将目标变量转换成因子型 set.seed(1234) # 设置随机种子 # 数据集随机抽70%定义为训练数据集,30%为测试数据集 ind <- sample(2, nrow(Data), replace = TRUE, prob = c(0.7, 0.3)) traindata <- Data[ind == 1, ] testdata <- Data[ind == 2, ] # 使用naiveBayes函数建立朴素贝叶斯分类模型 library(e1071) # 加载e1071包 naiveBayes.model <- naiveBayes(流失 ~ ., data = traindata) # 建立朴素贝叶斯分类模型 # 预测结果 train_predict <- predict(naiveBayes.model, newdata = traindata) # 训练数据集 test_predict <- predict(naiveBayes.model, newdata = testdata) # 测试数据集 # 输出训练数据的分类结果 train_predictdata <- cbind(traindata, predictedclass = train_predict) # 输出训练数据的混淆矩阵 (train_confusion <- table(actual = traindata$流失, predictedclass = train_predict)) # 输出测试数据的分类结果 test_predictdata <- cbind(testdata, predictedclass = test_predict) # 输出测试数据的混淆矩阵 (test_confusion <- table(actual = testdata$流失, predictedclass = test_predict)) # 使用NaiveBayes函数建立朴素贝叶斯分类模型 install.packages("klaR") library(klaR) # 加载klaR包 NaiveBayes.model <- NaiveBayes(流失 ~ ., data = traindata) # 建立朴素贝叶斯分类模型 # 预测结果 train_predict <- predict(NaiveBayes.model) # 训练数据集 test_predict <- predict(NaiveBayes.model, newdata = testdata) # 测试数据集 # 输出训练数据的分类结果 train_predictdata <- cbind(traindata, predictedclass = train_predict$class) # 输出训练数据的混淆矩阵 (train_confusion <- table(actual = traindata$流失, predictedclass = train_predict$class)) # 输出测试数据的分类结果 test_predictdata <- cbind(testdata, predictedclass = test_predict$class) # 输出测试数据的混淆矩阵 (test_confusion <- table(actual = testdata$流失, predictedclass = test_predict$class)) |


【lda模型】
Eg.1:建立lda模型并进行分类预测
| Data[, "流失"] <- as.factor(Data[, "流失"]) #将目标变量转换成因子型 set.seed(1234) # 设置随机种子 # 数据集随机抽70%定义为训练数据集,30%为测试数据集 ind <- sample(2, nrow(Data), replace = TRUE, prob = c(0.7, 0.3)) traindata <- Data[ind == 1, ] testdata <- Data[ind == 2, ] # 建立lda分类模型 install.packages("MASS") library(MASS) lda.model <- lda(流失 ~ ., data = traindata) # 预测结果 train_predict <- predict(lda.model, newdata = traindata) # 训练数据集 test_predict <- predict(lda.model, newdata = testdata) # 测试数据集 # 输出训练数据的分类结果 train_predictdata <- cbind(traindata, predictedclass = train_predict$class) # 输出训练数据的混淆矩阵 (train_confusion <- table(actual = traindata$流失, predictedclass = train_predict$class)) # 输出测试数据的分类结果 test_predictdata <- cbind(testdata, predictedclass = test_predict$class) # 输出测试数据的混淆矩阵 (test_confusion <- table(actual = testdata$流失, predictedclass = test_predict$class)) |

【rpart模型】
Eg.1:构建rpart模型并进行分类预测
| Data[, "流失"] <- as.factor(Data[, "流失"]) # 将目标变量转换成因子型 set.seed(1234) # 设置随机种子 # 数据集随机抽70%定义为训练数据集,30%为测试数据集 ind <- sample(2, nrow(Data), replace = TRUE, prob = c(0.7, 0.3)) traindata <- Data[ind == 1, ] testdata <- Data[ind == 2, ] # 建立rpart分类模型 library(rpart) install.packages("rpart.plot") library(rpart.plot) rpart.model <- rpart(流失 ~ ., data = traindata, method = "class", cp = 0.03) # cp为复杂的参数 # 输出决策树图 rpart.plot(rpart.model, branch = 1, branch.type = 2, type = 1, extra = 102, border.col = "blue", split.col = "red", split.cex = 1, main = "客户流失决策树") # 预测结果 train_predict <- predict(rpart.model, newdata = traindata, type = "class") # 训练数据集 test_predict <- predict(rpart.model, newdata = testdata, type = "class") # 测试数据集 # 输出训练数据的分类结果 train_predictdata <- cbind(traindata, predictedclass = train_predict) # 输出训练数据的混淆矩阵 (train_confusion <- table(actual = traindata$流失, predictedclass = train_predict)) # 输出测试数据的分类结果 test_predictdata <- cbind(testdata, predictedclass = test_predict) # 输出测试数据的混淆矩阵 (test_confusion <- table(actual = testdata$流失, predictedclass = test_predict)) |


【bagging模型】
Eg.1:构建bagging模型并进行分类预测
| Data[, "流失"] <- as.factor(Data[, "流失"]) # 将目标变量转换成因子型 set.seed(1234) # 设置随机种子 # 数据集随机抽70%定义为训练数据集,30%为测试数据集 ind <- sample(2, nrow(Data), replace = TRUE, prob = c(0.7, 0.3)) traindata <- Data[ind == 1, ] testdata <- Data[ind == 2, ] # 建立bagging分类模型 install.packages("adabag") library(adabag) bagging.model <- bagging(流失 ~ ., data = traindata) # 预测结果 train_predict <- predict(bagging.model, newdata = traindata) # 训练数据集 test_predict <- predict(bagging.model, newdata = testdata) # 测试数据集 # 输出训练数据的分类结果 train_predictdata <- cbind(traindata, predictedclass = train_predict$class) # 输出训练数据的混淆矩阵 (train_confusion <- table(actual = traindata$流失, predictedclass = train_predict$class)) # 输出测试数据的分类结果 test_predictdata <- cbind(testdata, predictedclass = test_predict$class) # 输出测试数据的混淆矩阵 (test_confusion <- table(actual = testdata$流失, predictedclass = test_predict$class)) |

【randomForest模型】
Eg.1:构建randomForest模型并进行分类预测
| Data[, "流失"] <- as.factor(Data[, "流失"]) # 将目标变量转换成因子型 set.seed(1234) # 设置随机种子 # 数据集随机抽70%定义为训练数据集,30%为测试数据集 ind <- sample(2, nrow(Data), replace = TRUE, prob = c(0.7, 0.3)) traindata <- Data[ind == 1, ] testdata <- Data[ind == 2, ] # 建立randomForest模型 install.packages("randomForest") library(randomForest) randomForest.model <- randomForest(流失 ~ ., data = traindata) # 预测结果 test_predict <- predict(randomForest.model, newdata = testdata) # 测试数据集 # 输出训练数据的混淆矩阵 (train_confusion <- randomForest.model$confusion) # 输出测试数据的混淆矩阵 (test_confusion <- table(actual = testdata$流失, predictedclass = test_predict)) |

【svm模型】
Eg.1:构建svm模型并进行分类预测
| Data[, "流失"] = as.factor(Data[, "流失"]) # 将目标变量转换成因子型 set.seed(1234) # 设置随机种子 # 数据集随机抽70%定义为训练数据集,30%为测试数据集 ind <- sample(2, nrow(Data), replace = TRUE, prob = c(0.7, 0.3)) traindata <- Data[ind == 1, ] testdata <- Data[ind == 2, ] # 建立svm模型 install.packages("e1071") library(e1071) svm.model <- svm(流失 ~ ., data = traindata) # 预测结果 train_predict <- predict(svm.model, newdata = traindata) # 训练数据集 test_predict <- predict(svm.model, newdata = testdata) # 测试数据集 # 输出训练数据的分类结果 train_predictdata <- cbind(traindata, predictedclass = train_predict) # 输出训练数据的混淆矩阵 (train_confusion <- table(actual = traindata$流失, predictedclass = train_predict)) # 输出测试数据的分类结果 test_predictdata <- cbind(testdata, predictedclass = test_predict) # 输出测试数据的混淆矩阵 (test_confusion <- table(actual = testdata$流失, predictedclass = test_predict)) |

【ROC曲线和PR曲线】
Eg.1:ROC曲线和PR曲线图代码
| install.packages("ROCR") library(ROCR) library(gplots) # 预测结果 train_predict <- predict(lda.model, newdata = traindata) # 训练数据集 test_predict <- predict(lda.model, newdata = testdata) # 测试数据集 par(mfrow = c(1, 2)) # ROC曲线 # 训练集 predi <- prediction(train_predict$posterior[, 2], traindata$流失) perfor <- performance(predi, "tpr", "fpr") plot(perfor, col = "red", type = "l", main = "ROC曲线", lty = 1) # 训练集的ROC曲线 # 测试集 predi2 <- prediction(test_predict$posterior[, 2], testdata$流失) perfor2 <- performance(predi2, "tpr", "fpr") par(new = T) plot(perfor2, col = "blue", type = "l", pch = 2, lty = 2) # 测试集的ROC曲线 abline(0, 1) legend("bottomright", legend = c("训练集", "测试集"), bty = "n", lty = c(1, 2), col = c("red", "blue")) # 图例 # PR曲线 # 训练集 perfor <- performance(predi, "prec", "rec") plot(perfor, col = "red", type = "l", main = "PR曲线", xlim = c(0, 1), ylim = c(0, 1), lty = 1) # 训练集的PR曲线 # 测试集 perfor2 <- performance(predi2, "prec", "rec") par(new = T) plot(perfor2, col = "blue", type = "l", pch = 2, xlim = c(0, 1), ylim = c(0, 1), lty = 2) # 测试集的PR曲线 abline(1, -1) legend("bottomleft", legend = c("训练集", "测试集"), bty = "n", lty = c(1, 2), col = c("red", "blue")) # 图例 |

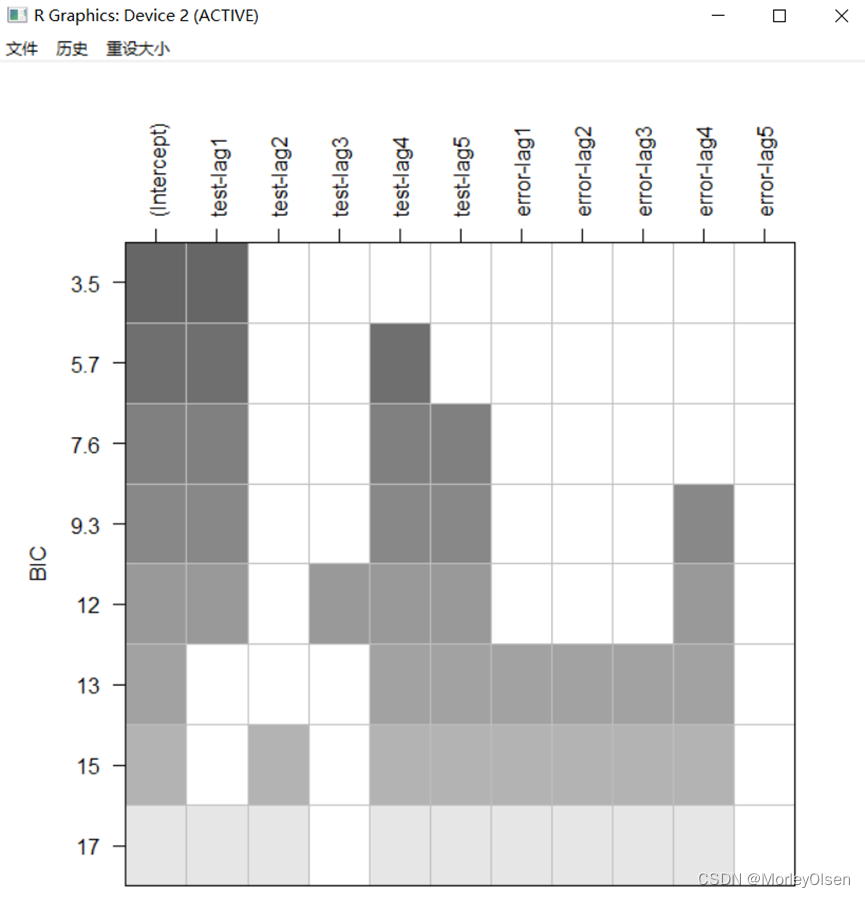
【BIC图和一阶差分】
Eg.1:
| install.packages("TSA") library(TSA) Data <- read.csv("arima_data.csv", header = T,fileEncoding = "GB2312")[, 2] sales <- ts(Data) plot.ts(sales, xlab = "时间", ylab = "销量 / 元") # 一阶差分 difsales <- diff(sales) # BIC图 res <- armasubsets(y = difsales, nar = 5, nma = 5, y.name = 'test', ar.method = 'ols') plot(res) |

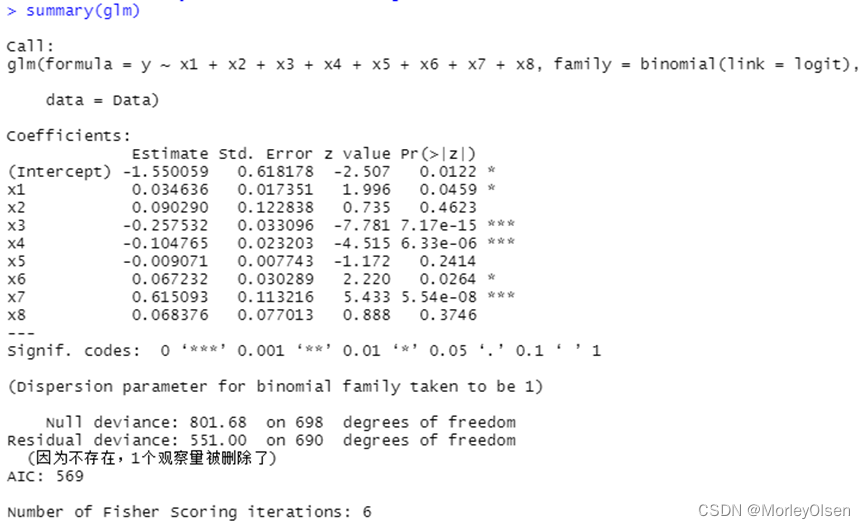
【逻辑回归】
Eg.1:
| Data <- read.csv("bankloan.csv",fileEncoding = "GB2312")[2:701, ] # 数据命名 colnames(Data) <- c("x1", "x2", "x3", "x4", "x5", "x6", "x7", "x8", "y") # logistic回归模型 glm <- glm(y ~ x1 + x2 + x3 + x4 + x5 + x6 + x7 + x8, family = binomial(link = logit), data = Data) summary(glm) # 逐步寻优法 logit.step <- step(glm, direction = "both") summary(logit.step) # 前向选择法 logit.step <- step(glm, direction = "forward") summary(logit.step) # 后向选择法 logit.step <- step(glm, direction = "backward") summary(logit.step) |







【ID3_decision_tree】
Eg.1:
| data <- read.csv("sales_data.csv",fileEncoding = "GB2312")[, 2:5] # 数据命名 colnames(data) <- c("x1", "x2", "x3", "result") # 计算一列数据的信息熵 calculateEntropy <- function(data) { t <- table(data) sum <- sum(t) t <- t[t != 0] entropy <- -sum(log2(t / sum) * (t / sum)) return(entropy) } # 计算两列数据的信息熵 calculateEntropy2 <- function(data) { var <- table(data[1]) p <- var/sum(var) varnames <- names(var) array <- c() for (name in varnames) { array <- append(array, calculateEntropy(subset(data, data[1] == name, select = 2))) } return(sum(array * p)) } buildTree <- function(data) { if (length(unique(data$result)) == 1) { cat(data$result[1]) return() } if (length(names(data)) == 1) { cat("...") return() } entropy <- calculateEntropy(data$result) labels <- names(data) label <- "" temp <- Inf subentropy <- c() for (i in 1:(length(data) - 1)) { temp2 <- calculateEntropy2(data[c(i, length(labels))]) if (temp2 < temp) { temp <- temp2 label <- labels[i] } subentropy <- append(subentropy,temp2) } cat(label) cat("[") nextLabels <- labels[labels != label] for (value in unlist(unique(data[label]))) { cat(value,":") buildTree(subset(data,data[label] == value, select = nextLabels)) cat(";") } cat("]") } # 构建分类树 buildTree(data) |

【bp_neural_network】
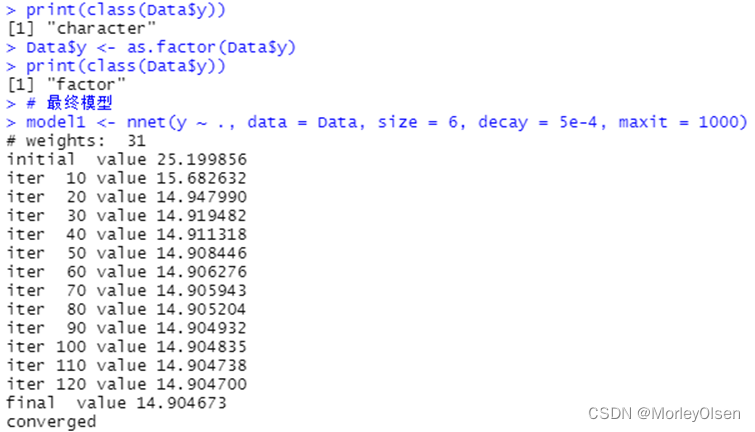
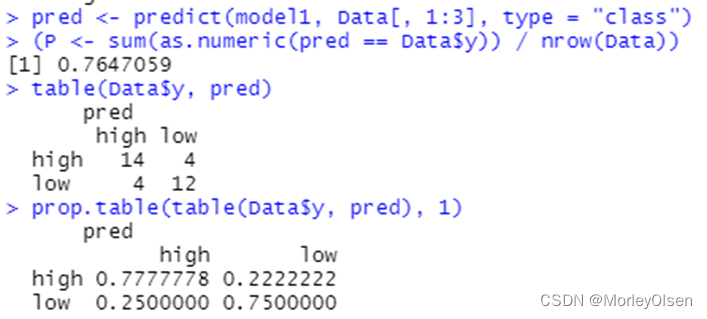
Eg.1:
| Data <- read.csv("sales_data.csv",fileEncoding = "GB2312")[, 2:5] # 数据命名 library(nnet) colnames(Data) <- c("x1", "x2", "x3", "y") print(names(Data)) print(class(Data$y)) Data$y <- as.factor(Data$y) print(class(Data$y)) # 最终模型 model1 <- nnet(y ~ ., data = Data, size = 6, decay = 5e-4, maxit = 1000) pred <- predict(model1, Data[, 1:3], type = "class") (P <- sum(as.numeric(pred == Data$y)) / nrow(Data)) table(Data$y, pred) prop.table(table(Data$y, pred), 1) |