今天让我们来看看整型的数据和浮点型的数据在内存中是怎么存储的呢
整型数据在内存中的存储
整型数据在内存中存储的是二进制的补码
正数的话也没什么可说的,原码反码补码都相同
我们来看看负数:
以-5为例
原码:10000000 00000000 00000000 00000101
反码:11111111 11111111 11111111 11111010
补码:11111111 11111111 11111111 11111011
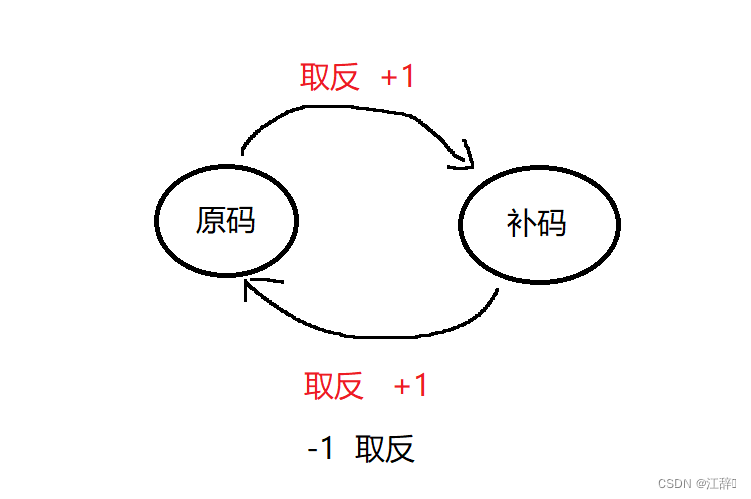
负数的反码就是符号位不变,其他位按位取反。负数的补码就是反码+1.
为什么内存要存补码?
在计算机系统中,数值一律使用补码的方式来表示和储存。我们使用补码的原因在于,使用补码可以将符号位和数值域统一处理。
同时,加法和减法也可以使用补码来统一处理,因为CPU中其实只有加法器。
此外,补码与原码相互转换,它们的运算过程是相同的,不需要额外的硬件电路去进行补码到原码的额外转换;大致情况如图:
我们还是以-5为例
原码: 10000000 00000000 00000000 00000101
补码: 11111111 11111111 11111111 11111011
补码取反: 10000000 00000000 00000000 00000100
加一: 10000000 00000000 00000000 00000101
我们通过运算可以看到,结果无误,补码取反加一之后确实可以得到原码。
其实在我们之前的一篇博客中解释过了大小端存储,我们使用的vs2022使用的就是小端字节序存储方式。
还是以-5为例

我们通过程序的调试可以发现,在a的地址0x012ff87c中a存储的值为fb ff ff ff,那么我们再来看看-5的补码:
补码:11111111 11111111 11111111 11111011
十六进制为:ff ff ff fb
十六进制数中1111(十进制为15)是f,1011(十进制为11)是b
小端存储方式是数据的高位存储在高地址,数据的低位存储在低地址,这里也印证了我们之前的结论。
了解了整型在内存中的存储,我们再来看看浮点型在内存中是怎么存储的吧
浮点型数据在内存中的存储
在了解浮点型存储方式之前,想邀请大家来猜一猜以下的代码输出的值都是多少
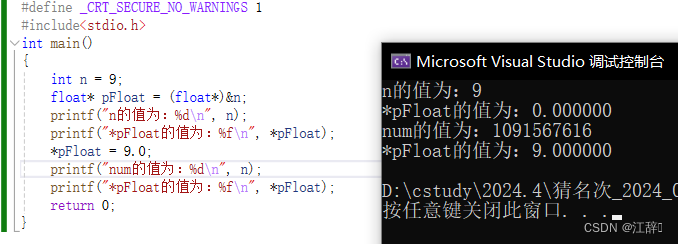
int main()
{int n = 9;float *pFloat = (float *)&n;printf("n的值为:%d\n",n);printf("*pFloat的值为:%f\n",*pFloat);*pFloat = 9.0;printf("num的值为:%d\n",n);printf("*pFloat的值为:%f\n",*pFloat);return 0;
}大家要好好想一想哦
浮点型存储的标准
既然这里这样说了,那么我们就了解浮点型与整型在内存中的存储方式肯定是不一样的了,那我们来看看浮点型存储的标准
根据国际标准IEEE(电气和电子工程协会)754规定,任意一个二进制浮点数V可以表示成下面的形式:
(-1)^S*M*2^E
-1^S表示符号位,当S=0,V是正数;当S=1,V为负数。
M表示有效数字,M表示的值大于等于1,小于2。就是将数字变为科学计数法
2^E表示指数位
大家是不是一脸懵逼啊,我刚刚看到的时候也是,给大家举几个例子理解一下
假设V=5.5
二进制表示:101.1
在转换为2进制的时候要注意小数点之后的权重,从小数点第一位开始,往后的权重依次为2^-1,2^-2,2^-3......
这里我们来看,有效数字M要求是大于等于1,小于2,那么我们这里就需要将101.1的小数点往前移动两位可以达到要求,那么我们这里就变为了1.011*2^2,我们这里是2进制数字,乘的底数就为2,小数点往前移几位,咋们就乘2的多少次方。
这里我们基本上就解决了,那么我们的V应该怎么写呢
V=5.5=(-1)^0*1.011*2^2
S=0(数字为正数)
M = 1.011(有效数字)
E = 2
IEEE 754 规定
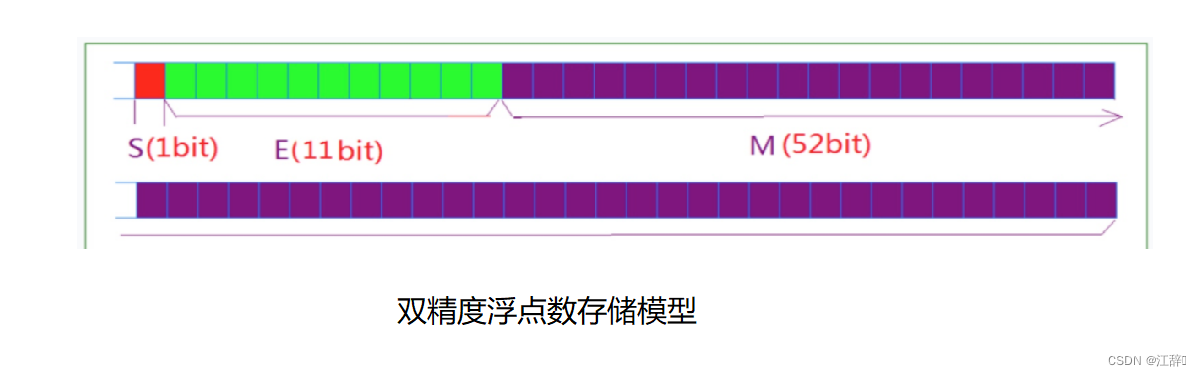
在内存中,对于32位的浮点数,最高的1位是符号位s,接着的8位是指数E,剩下的23位为有效数字M。
图示:

对于64位的浮点数,最高一位是符号位S,接着的11位是指数E,剩下的52位为指数S。
有效数字M
有效数字M,我们M的值只能是1~2之间的话,那么我们表示M就可以使用1.xxxxxx的形式,xxxxxx表示小数部分
IEEE 754 规定,在计算机内部保存M的时候,默认这个数的第一位总是1,因此可以被舍去,只保存后面的xxxxxx部分。
比如保存1.01的时候,我们可以直接保存01,等到我们需要读取的时候,再把第一位加上去。我们这样做的目的是,节省一位有效数字。以32位浮点数为例,留给M的只有23位,我们将第一位舍弃之后,就可以保存24位的有效数字
指数E的复杂情况
首先我们需要了解的是E的类型是unsigend int类型,它是一个无符号整数,那么这意味着,当E在单精度浮点型里为8位的时候它的取值是0~255,但是我们知道在科学计数法中,E是可以出现负数的,那么我们针对这个问题IEEE 754规定,输入内存时E的真实值必须再加上一个中间数,对于8位E,这个中间数为127,11位的话是1023。
那么当我们要在内存中存的e为10的时候,我们需要将10+127,存放137进入内存,E=10001001。
之后指数E从内存中取出还要分3种情况
E不全为0或E不全为1
这时浮点数采用以下规则表示,即指数E的计算减去127(或1023),得到真实值,之后将有效数字M前加上第一位的1.
例如:
0.5的二进制表示为0.1,由于规定正数部分必须为1,即将小数点右移一位,则为1.0*2^(-1),其阶码为-1+127=126,表示为:01111110,而尾数部分去掉整数部分为0,补齐0到23位00000000000000000000000,则其二进制表示为
0 01111110 00000000000000000000000
E全为0
这个时候,浮点数的指数e等于1-127或者(1-1023)即为真实值,有效数字M不再加上第一位的1,而是还原成0.xxxxxx的小数。这样是为了表示+-0,以及接近与0的很小的数字。
E全为1
这时,如果有效数字M全为0,表示+-无穷大,正负取决于符号位s。
现在大家对之前的题有答案了嘛
我们来看看
代码运行结果
疑问与下回分解
在n=9的时候为什么*pFloat的值会是0.000000呢?为什么num的值会那么大呢?为什么在n的值为9.0 的时候*pFloat的值会是9.000000呢?
写不动喽,我们有很多疑问,大家可以先消化一下今天的知识,我们每天再来为大家详细解释。