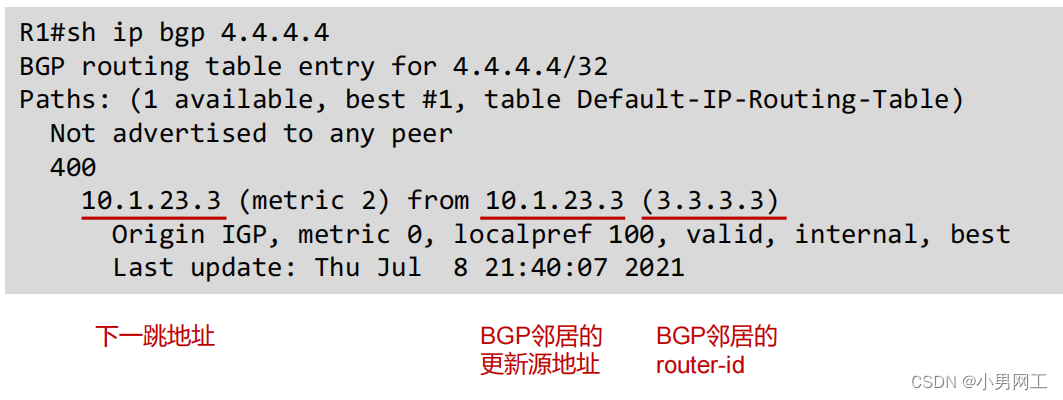
在介绍 堆 和 加强堆 的文章中,我们探讨了当有新的元素加入时,如何实时更新前 K 个元素的方法。
(还没学习过的小伙伴赶快关注,在 「堆」 合集里查看哦!)
今天我们介绍一种新的方法,使用 bfptr 算法求解第 K 小(大) 的数。
BFPTR 算法
BFPRT 是一种 改进版 的 快速排序 算法。
为什么说是改进版的快排呢?简单回顾一下 快排 的步骤:
- 随机选择一个元素(或者当前划分的首或尾元素)作为初始的 基准元素 。
- 遍历每个元素并与基准元素进行比较:
- 所有比基准值 小 的元素放在左侧;
- 所有比基准值 大 的元素放在右侧;
- 中间位置是所有与基准元素 相等 的元素。
- 对左右两部分分别递归进行快速排序。
其时间复杂度为 O ( N l o g N ) O(NlogN) O(NlogN),但最坏情况下的时间复杂度退化为 O ( n 2 ) O(n^2) O(n2) 。
原因在于如果选择的基准值“太偏”时,两侧未排好的元素数量不均匀,起不到快排的效果,时间复杂度退化为了 O ( n 2 ) O(n^2) O(n2) 。
因此,选择一个好的基准元素至关重要,BFPRT算法 就是 用来选择一个较好的基准元素,避免最坏情况的产生。
选取原则
- 将待排序的数组按 5 个元素一组进行分组,最后不足 5 个的也划分到新的一组中。
- 将每一个小组中的 5 个元素进行排序,并取第 3 个元素(即 5 个元素的中位数)。最后一组若有偶数个元素,取上中位数。
- 将得到的每组的中位数再次进行排序,取其中位数作为本次划分的基准元素。
- 选好基准元素后,剩下的步骤同快速排序。
因此,BFPTR 算法又叫做 中位数的中位数算法 ,其实就是对快速排序第一步中 如何选择基准元素 进行了一定的改进和优化,其它步骤与快速排序无任何差别。
提示:对于 5 个元素的排序,选择最简单的 插入排序 即可。
主要代码
// bfprt 算法
public static void minKth(int[] array, int k) {// 拷贝一份,不破坏原有数组int[] arr = copyArray(array);// 第 k 小的数,下标为 k-1int ans = bfprt(arr, 0, arr.length - 1, k - 1);System.out.println(ans);
}// 如果 arr[L..R] 有序时,返回 index 位置上的数
public static int bfprt(int[] arr, int L, int R, int index) {if (L == R) {return arr[L];}// 划分 基准元素int pivot = medianOfMedians(arr, L, R);// 对 pivot 元素进行快排划分// 返回等于 pivot 元素的范围下标[L,R]数组int[] range = partition(arr, L, R, pivot);// 下标index 在 等于 pivot 元素的范围下标[L,R] 中,直接返回if (index >= range[0] && index <= range[1]) {return arr[index];} else if (index < range[0]) {// 对左侧继续递归return bfprt(arr, L, range[0] - 1, index);} else {// 对右侧继续递归return bfprt(arr, range[1] + 1, R, index);}
}
以上部分其实就是改进过后的快速排序代码,无需对所有的元素进行排序,只需对左右其中一侧进行递归排序,直至找到下标 index (即 k-1 下标)元素。
划分代码
// 选择中位数的中位数
public static int medianOfMedians(int[] arr, int L, int R) {int size = R - L + 1;// 判断是否有不足 5 个为一组的int offset = size % 5 == 0 ? 0 : 1;int[] mArr = new int[size / 5 + offset];// 每 5 个一组的中位数计入mArr中for (int team = 0; team < mArr.length; team++) {// 计算每组的起始位置int teamFirst = L + team * 5;// 起始位置teamFirst 到结尾位置teamFirst + 4这一组进行插入排序// 若最后不足 5 个了,结尾位置为 RmArr[team] = getMedian(arr, teamFirst, Math.min(R, teamFirst + 4));}// 再求 mArr 的中位数,即 mArr.length / 2 位置上的数是几return bfprt(mArr, 0, mArr.length - 1, mArr.length / 2);
}// 返回排序后的中位数
public static int getMedian(int[] arr, int L, int R) {insertionSort(arr, L, R);return arr[(L + R) / 2];
}// 插入排序
public static void insertionSort(int[] arr, int L, int R) {for (int i = L + 1; i <= R; i++) {for (int j = i - 1; j >= L && arr[j] > arr[j + 1]; j--) {swap(arr, j, j + 1);}}
}
函数间的调用有点儿多,仔细理解每个函数的功能,相信小伙伴能够轻松搞懂代码逻辑。
该算法的时间复杂度为:
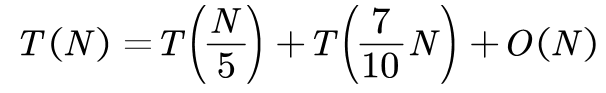
能够证明出,上述式子的时间复杂度为 O ( N ) O(N) O(N) 。具体的推导及证明过程,感兴趣的小伙伴可以参照《算法导论》 9.3节 Selection in worst-case linear time 的内容进行理解。关注回复「算法导论」 获取该书籍。

虽然证明出了该方法避免了最坏的时间复杂度,但其实使用最初的快速排序也不会太差,ACM算法竞赛入门这本书中提到了这样的一句话:实践中几乎不可能达到最坏情况。 在 O ( N ) O(N) O(N)的时间复杂度内能够求出第 k 大(小)的元素。关注回复「ACM紫书」 获取该书籍。


~ 点赞 ~ 关注 ~ 星标 ~ 不迷路 ~!!!
回复「ACM紫书」获取 ACM 算法书籍 ~
回复「算法导论」获取 算法导论第3版 ~









![[Java EE] 多线程(五):单例模式与阻塞队列](https://img-blog.csdnimg.cn/direct/f0735e2549b642828382bde20623bbca.png)