数量分析方法(四)
- 常见概率分布
- 基本概念
- 离散型随机变量与连续型随机变量
- 离散型随机变量
- 连续型随机变量
- 分布函数
- 概率密度函数(PDF)
- 累积分布函数(CDF)
- 离散分布
- 离散均匀分布
- 伯努利分布
- 二项分布
- 定义
- 股价二叉树
- 连续分布
- 连续均匀分布
- 正态分布
- 基本概念与性质
- 标准正态分布及其应用
- 亏空风险
- 罗伊安全第一比例
- 对数正态分布
- 学生t分布
- 多元分布
- 模拟
- 蒙特卡洛模拟
- 历史法模拟
常见概率分布
基本概念
离散型随机变量与连续型随机变量
随机变量依据结果分布状况分为两种:离散型随机变量与连续型随机变量,其对应概率分布分别为离散分布与连续分布。
离散型随机变量
当随机变量的取值结果是可数的时候,则称其为离散型随机变量。可数具有两层含义:随机变量的可能取值要么是有限的,要么是无限但可数的。例如,抛骰子实验中,骰子的点数记为随机变量X,X的可能取值是有限的,即{1,2,3,4,5,6},因此随机变量X是离散的。又如,记某一天内来某银行办理业务的人数为随机变量Y,Y的可能取值虽然是无限多个,但可以逐个数出,即{0,1,2,…},因此随机变量Y也是离散的。这里需要注意,一天内来银行办理业务的人数可以是任意大的非负整数,只是较大正整数的取值概率极小而已。换言之,可数的数学含义即可用自然数下标把所有可能结果列出,如{y1,y2,…,yn,…}。反之,如果随机变量的可能取值在某一连续区间内,而不是离散开来的,则该随机变量就不是离散的。
连续型随机变量
当随机变量的可能取值为无限且不可数时,则称其为连续型随机变量。换言之,连续型随机变量的可能取值可以充满某个区间。例如,记某一天某地的降雨量为随机变量Y,Y的取值范围为[0,+∞],则随机变量Y为连续型随机变量有一些特殊规定与性质:
- 连续型随机变量的取值范围通常为某一区间,即使区间存在上下界,可能取值仍然为无穷多个;
- 由于连续型随机变量的可能取值结果是无穷多个,相应地每一点对应的概率可以近似看成为 P ( Y = y ) = 1 ∞ = 0 P(Y=y)=\frac 1 \infty=0 P(Y=y)=∞1=0。
- 在研究一些问题时,可以把离散变量近似看成连续型随机变量。例如,某股票当天收盘价为10元,假设10%的涨停板,第二天收盘价的取值范围[9,11]。然而,由于交易所要求股票报价的最小单位为“分”,即股票报价最多精确到两位数,不可能有10.001元。因此Z的取值是一个有限的离散型随机变量。即{9.00,9.01,9.02,…,10.00}。但为了研究方便,我们通常也将Z看成是连续型随机变量。
分布函数
概率密度函数(PDF)
概率密度函数就是对某个随机变量的所有可能取值及对应概率进行描述的函数。对于离散型随机变量而言,描述其概率分布最简单并且最直观的方法就是通过表格的方式,把每一可能取值对应的概率逐一列出。当随机变量X取值xi时对应的概率记为p(xi)。
| 随机变量X | X=x1 | X=x2 | … | X=xn | … |
|---|---|---|---|---|---|
| 取值概率 | p(x1) | p(x2) | … | p(xn) | … |
有些情形下p(xi)可以写成函数形式,则p(xi)即为离散型随机变量的概率函数。例如,假定随机变量X可能取值为{1,2,3,4,5},概率密度函数为p(x)=x/15。那么X=3的概率就是3/15=20%。此外,p(x)非负,且有1/15+2/15+…+5/15=1。p(x)符合概率的基本定义。
对于连续型随机变量,由于取值不可列,无法采用逐一列示的方法来描述概率分布。因此。研究连续型随机变量时,关注的是随机变量在某一区间内的概率,而不是某一点的概率。例如,研究股价恰好是10.02元还是10.03元、降雨量恰好是2000002毫米等问题是没有意义的(连续型随机变量取某一单点的概率都是0),更值得关注的是股价在[10.00,10.30]元范围内的概率是多少,降雨量在[20,30]毫米之间的概率是多少。计算区间概率就要引入连续型随机变量的概率密度函数。
连续型随机变量PDF有以下几个性质:
- 概率密度函数通常用f(x)表示,函数图像与x轴上区间[x1,x2]围成的面积即代表随机变量X在区间[x1,x2]内的概率;此面积实际上即为 ∫ x 1 x 2 f ( x ) d x \int_{x_1}^{x_2}f(x)dx ∫x1x2f(x)dx。
- 概率密度函数f(x)非负且与x轴围成的面积为1(与概率的定义相对应)。
- 由于连续型随机变量取任意单点的概率为0,所以在研究连续型随机变量时,区间是开区间还是闭区间是无所谓的。
累积分布函数(CDF)
累积分布函数,顾名思义代表“累积”的概率,即随机变量X小于某特定值x的概率,通常记为F(x)=P(X≤x)。由累积分布函数的定义可直接得到CDF的几条性质:
- 累积分布函数是有界的,即 F ( − ∞ ) = P ( X ≤ − ∞ ) = 0 F(-\infin)=P(X\le-\infin)=0 F(−∞)=P(X≤−∞)=0, F ( + ∞ ) = P ( X ≤ + ∞ ) = 1 F(+\infin)=P(X\le+\infin)=1 F(+∞)=P(X≤+∞)=1;
- 累积分布函数是单调递增的,即如果 x 1 ≤ x 2 x_1\le{x_2} x1≤x2,则 F ( x 1 ) ≤ F ( x 2 ) F(x_1)\le{F(x_2)} F(x1)≤F(x2);
- P ( x 1 < X ≤ x 2 ) = P ( X ≤ x 2 ) − P ( X ≤ x 1 ) = F ( x 2 ) − F ( x 1 ) P(x_1<X \le x_2)=P(X \le x_2)-P(X \le x_1)=F(x_2)-F(x_1) P(x1<X≤x2)=P(X≤x2)−P(X≤x1)=F(x2)−F(x1);
- 离散型随机变量的累积分布函数呈现出阶梯状;
- 连续型概率密度函数(PDF)与累积分布函数(CDF)的关系见下图。
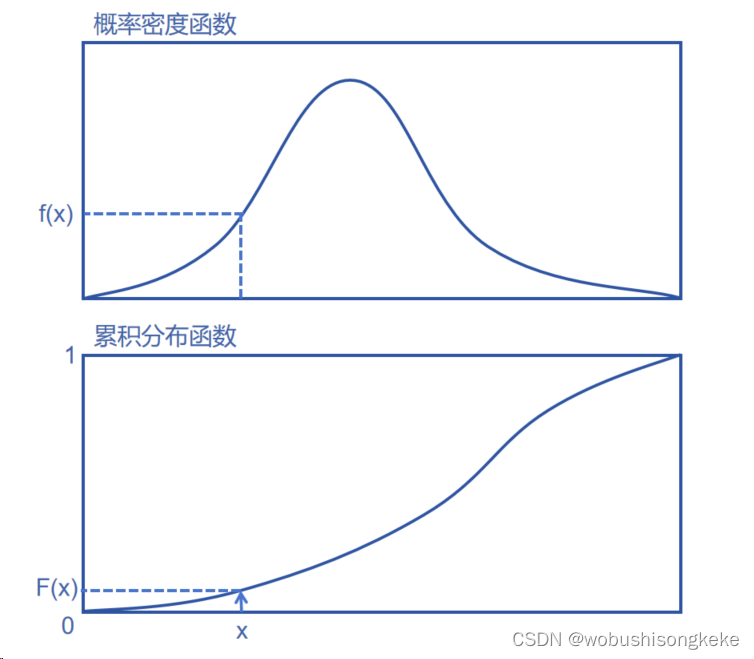
上图为概率密度函数f(x),下图为累积分布函数F(x)。其中,F(x)是单调递增,且上界为1,下界为0.由于 F ( x ) = P ( X ≤ x ) F(x)=P(X\le x) F(x)=P(X≤x),因此F(x)在下图中的取值实际上就是上图中f(x)函数与区间(-∞,x)围成的面积。
离散分布
离散均匀分布
均匀分布是指随机变量的每个取值对应的概率是相等的,即“均匀”的。服从离散均匀分布的随机变量X有n个可能取值,即{x1,x2,…,xn},P(X=xj)=1/n。
伯努利分布
伯努利分布又称两点分布,是指随机变量X只有两个可能取值结果1与0。当X=1时代表“成功”,其对应概率为p;当X=0时,代表“失败”,对应概率为1-p。最典型的伯努利分布就是抛硬币实验,硬币正面朝上表示“成功”,即X=1对应概率为50%;硬币反面朝上表示“失败”,即X=0对应概率为50%。
二项分布
定义
如果将伯努利分布中的事件“成功”或“失败”看成一次试验的话,二项分布则就是度量进行n次伯努利实验,成功次数为X=x的概率(x为0到n之间的任意整数),记为B(n,p)。其中,n与p为二项分布的两个参数。二项分布隐含假定:
- 不同次试验是指相互独立的;
- 每次试验的成功概率为常数p。
一般地,定义随机变量X为n次伯努利试验中成功的次数,每次成功概率为p,则P(X=x)的概率为:
P ( x ) = C n x p x ( 1 − p ) n − x = n ! ( n − x ) ! x ! p x ( 1 − p ) n − x P(x)=C_n^xp^x(1-p)^{n-x}=\frac {n!} {(n-x)!x!}p^x(1-p)^{n-x} P(x)=Cnxpx(1−p)n−x=(n−x)!x!n!px(1−p)n−x
对于伯努利分布来说,进行一次伯努利试验成功概率为p,根据定义可求均值与方差为p即p(1-p)。对于二项分布来说,相当于进行n次伯努利试验,其均值与方差分别为n乘以伯努利分布的均值与方差,即np及np(1-p)。
| 均值 | 方差 | |
|---|---|---|
| 伯努利分布 | p | p(1-p) |
| 二项分布 | np | np(1-p) |
股价二叉树
在t=0时期,股票价格为S。为研究方便,假定每期股价只会有两种变动可能:(1)上涨(u-1)倍,对应概率为p;(2)下跌(1-d)倍,对应概率为1-p。3期后股价为uudS的概率为多少?(其中,u>1,d=1/u<1)
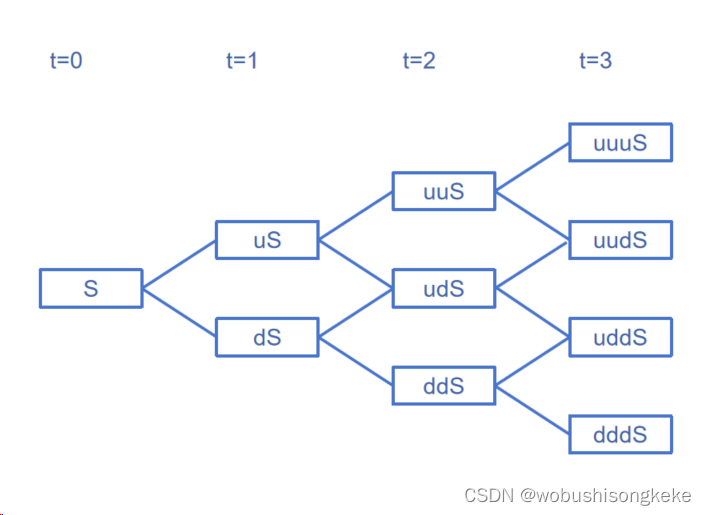
股价最终为uudS可以通过路径达到:udu、uud以及duu,固有:
P ( u u d S ) = 3 ! ( 3 − 2 ) ! ∗ 2 ! p 2 ( 1 − p ) P(uudS)=\frac {3!} {(3-2)!*2!}p^2(1-p) P(uudS)=(3−2)!∗2!3!p2(1−p)
连续分布
连续均匀分布
离散均匀分布是指随机变量每一取值的概率相等,连续均匀分布实际上也有类似的含义。然而,对于连续分布来说,每一单点概率都为0,因此“均匀”主要是针对区间而言,连续均匀分布的概率密度函数PDF为:
f ( x ) = { 1 b − a ( a ≤ x ≤ b ) 0 ( o t h e r w i s e ) f(x) = \begin{cases} \frac 1 {b-a} &\text (a \le x \le b) \\ 0 &\text (otherwise) \end{cases} f(x)={b−a10(a≤x≤b)(otherwise)
连续均匀分布的PDF图形见左图。可以看出,连续均匀分布的PDF在区间[a,b]为常数1/(b-a),超出这一范围取值均为0。随机变量X在[x1,x2]之间的概率为区间[x1,x2]与PDF围成的面积,这一面积实际就是长为(x2-x1)、高为1/(b-a)的矩形面积,即:
P ( x 1 ≤ X ≤ x 2 ) = x 2 − x 1 b − a P(x_1 \le X \le x_2)=\frac {x_2-x_1} {b-a} P(x1≤X≤x2)=b−ax2−x1
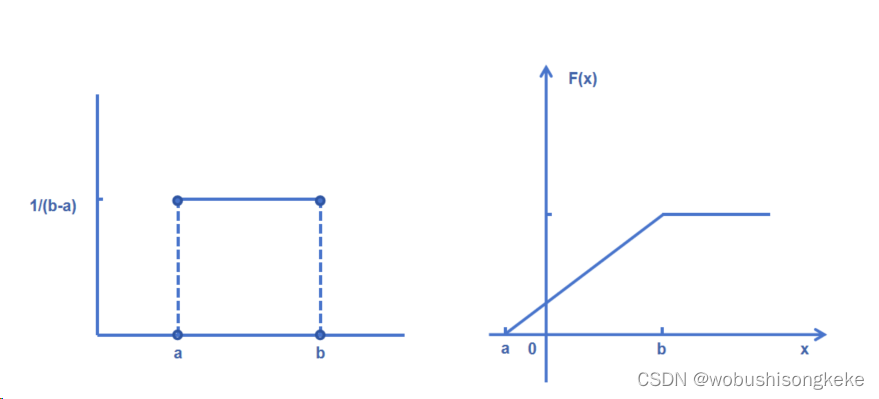
利用公式即可推导出连续均匀分布的累积分布函数。根据CDF的定义,F(x)即为P(X≤x)。当x在a与b之间时,利用公式有P(X≤x)即为(x-a)/(b-a)。而随机变量X在[a,b]范围之外概率均为0,故CDF图形如右图所示,其表达式为:
F ( x ) = { 0 ( x ≤ a ) x − a b − a ( a < x < b ) 1 ( x ≥ b ) F(x) = \begin{cases} 0 &\text ( x \le a) \\ \frac {x-a} {b-a} &\text (a<x<b) \\ 1 &\text (x \ge b) \end{cases} F(x)=⎩ ⎨ ⎧0b−ax−a1(x≤a)(a<x<b)(x≥b)
正态分布
基本概念与性质
正态分布可以说是概率论与数理统计中最重要的一个分部,同时也是在金融研究中运用最广泛的一个分布。在现实生活中很多随机变量的概率分布都可以用正态分布描述或近似描述。
正态分布的概率密度函数是一条钟形曲线,中间高两端低,左右关于其均值对称,两端无限延伸,见下图。
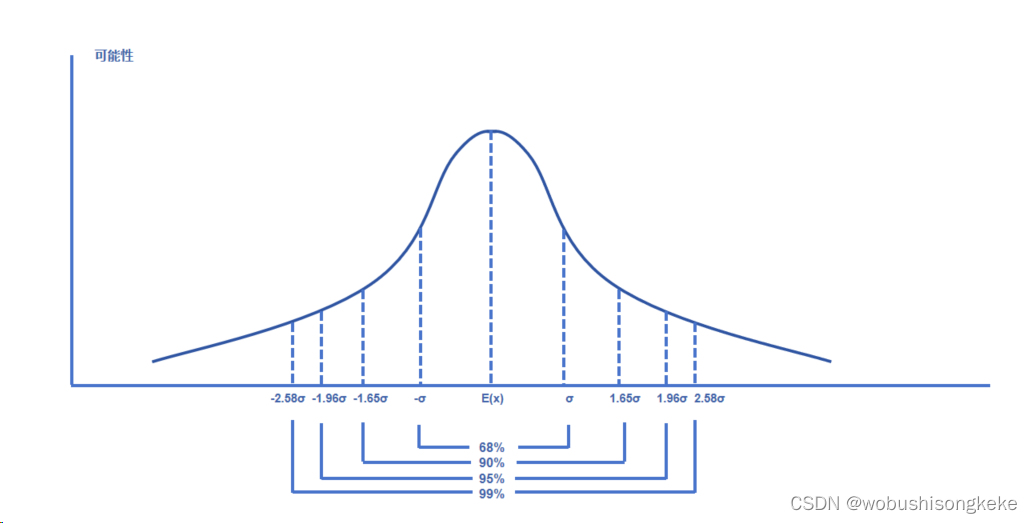
有关正态分布的PDF,重点掌握以下几点性质。
- 正态分布的PDF可由均值和方差完全刻画,通常记为N(μ,σ2)。其中μ表示均值,σ2表示方差。
- 根据PDF的图形,在均值μ附近取值的概率较大,而取极大值或极小值的概率较小。
- 正态分布的偏度为0,峰度为3。
- 服从正态分布且相互独立的随机变量的线性组合仍然服从正态分布。即如果随机变量X与随机变量Y均服从正态分布,则aX+bY也服从正态分布。
- 如果随机变量X服从正态分布,则有:
X落在[μ-σ,μ+σ]的概率为68%。
X落在[μ-1.65σ,μ+1.65σ]的概率为90%。
X落在[μ-1.96σ,μ+1.96σ]的概率为95%。
X落在[μ-2.58σ,μ+2.58σ]的概率为99%。
标准正态分布及其应用
如前所述,正态分布的PDF完全可以由其均值和方差所刻画。为了考察任一正态分布N(μ,σ2)有关事件的概率,需要引入标准正态分布。均值为0,方差为1的正态分布即为标准正态分布,通常称为Z分布。于是,通过标准正态分布表就可以计算任一正态分布N(μ,σ2)相关事件的概率了。
例如,已知随机变量X服从正态分布N(μ,σ2),则可以证明(X-μ)/σ服从标准正态分布Z(0,1)。因此有:
P ( X ≤ x ) = P ( X − μ σ ≤ x − μ σ ) = Φ ( x − μ σ ) P(X \le x)=P({\frac {X-\mu} {\sigma}}\le{\frac {x-\mu} {\sigma}})=\Phi(\frac {x-\mu} {\sigma}) P(X≤x)=P(σX−μ≤σx−μ)=Φ(σx−μ)
其中, Φ ( x ) \Phi(x) Φ(x)代表标准正态分布的CDF。
亏空风险
正态分布在现代资产组合理论中有着非常广泛地运用。例如,通常假设资产收益率服从正态分布,那么收益率的方差就衡量了资产收益率变动的风险。用方差来衡量风险主要是强调收益率的不确定性。这种不确定性即包括收益率低于均值的情况,也包括收益率高于均值的情况。然而,在有些情况下,投资者并不认为收益率高于均值的情况是风险,更想单独考察收益率低于某个特定水平的风险,这就要引入亏空风险的概念。
亏空风险是指资产收益率在一段时期内低于最低可接受水平RL的概率。注意,亏空风险是一个概率。如果资产收益率服从正态分布,亏空风险就是P(R<RL),也就是下图中阴影部分面积。
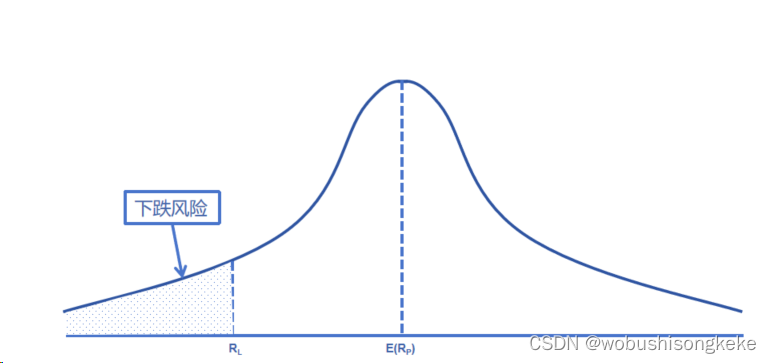
罗伊安全第一比例
对于投资者来说资产收益率低于RL是不可接受的,那么在进行投资时就必须最小化亏空风险P(R<RL)。投资者也可以通过最大化罗伊安全第一比例来实现这一目的。罗伊安全第一比例的公式为:
S F r a t i o = E ( R p ) − R L σ p , R L = S h o r t f a l l l e v e l SF \; ratio=\frac {E(R_p)-R_L} {\sigma_p},R_L=Shortfall\;level SFratio=σpE(Rp)−RL,RL=Shortfalllevel
其中,E(Rp)与σp分别为资产p收益率的均值与标准差。
对数正态分布
正态分布并不适用于描述资产价格。这是因为正态分布的取值范围在负无穷到正无穷之间,但资产价格不可能为负数。这就要引入对数正态分布。
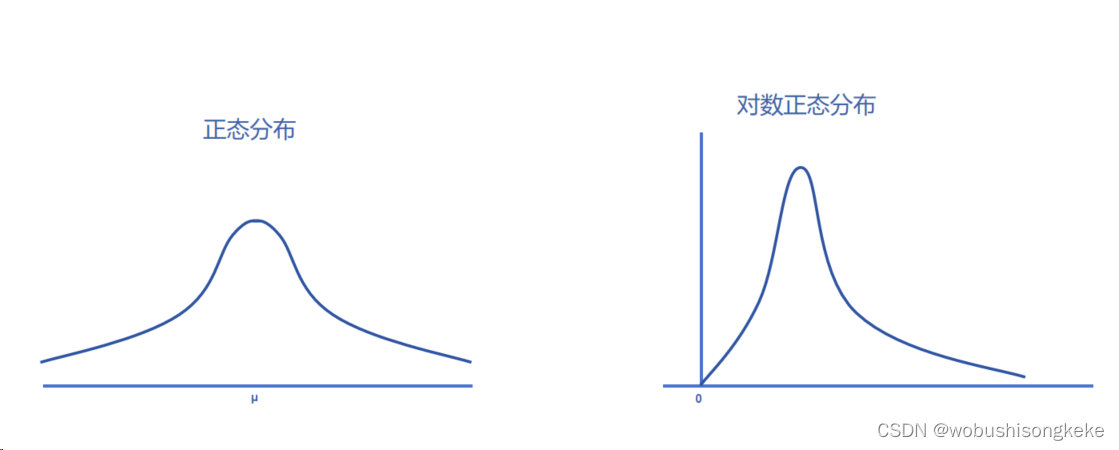
对数正态分布定义为:对于随机变量X,如果lnX服从正态分布,那么X服从对数正态分布。有关对数正态分布,主要需要掌握以下几点性质。
- 对数正态分布的概率密度函数是非负的;
- 对数正态分布的概率密度函数是正偏的;
- 对数正态分布是用来衡量资产价格的,而正态分布主要是用来衡量收益率的。
学生t分布
t分布是统计学中非常重要的一类分布,有英国统计学家哥赛特发现。当时哥赛特在一家酿酒厂担任检验师。在对酿酒数据进行分析时,哥赛特发现当样本容量较小时,实验数据并不服从正态分布,其概率分布形状与正态分布类似但尾部更厚。哥赛特以“Student”为笔名,发表了相关研究结果,因此后人将此分布称为学生t分布。t分布具有划时代意义,它打破了以往人们局限于正态分布的认知,开创了小样本统计推断的时代。
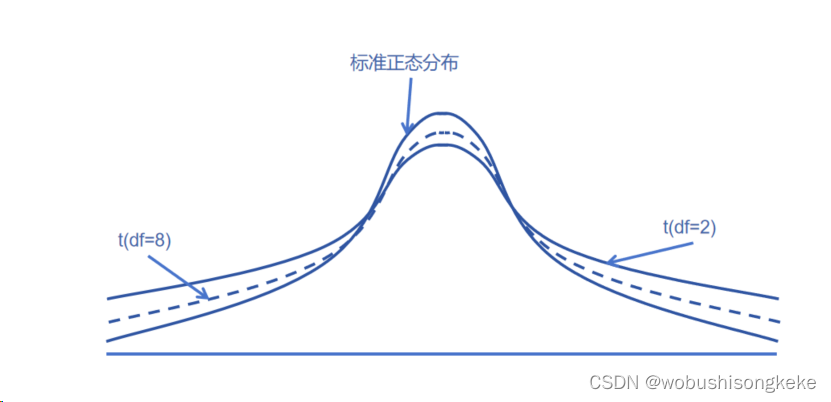
- t分布的概率密度函数可以由一个参数完全刻画:自由度,通常记为t(n)。其中n代表自由度,为正整数。
- t分布的概率密度函数也是一条钟形曲线,左右对称,但尾部比正态函数更厚(即偏度=0,峰度>3)。
- 当t分布的自由度增加并趋近于无穷大时,t分布的概率密度函数会无限趋近于标准正态分布的概率密度函数。
多元分布
目前为止,介绍的分布均为一元分布,即描述一个随机变量的概率分布。然而,基金经理在进行资产配置时,往往需要涉及多种资产,这就需要用到多元分布,用于衡量一组随机变量的概率分布。
利用多元正态分布可以衡量资产组合的概率分布。刻画多元正态分布只需知道三类参数:
- 资产组合中每个资产收益率的均值。
- 资产组合中每个资产收益率的方差。
- 资产组合中不同资产之间的相关系数。假设资产组合共有n个资产,那么需要知道的相关系数个数为 C n 2 = n ( n − 1 ) / 2 C_n^2=n(n-1)/2 Cn2=n(n−1)/2。
模拟
蒙特卡洛模拟
在经济金融研究中,很多情形是无法预估的,这就限制了传统统计学方法的分析范围。例如,1999年1月1日欧元诞生,这导致欧洲许多国家股票之间的相关系数大幅上升。为了防范系统性风险,许多经济金融学家会关注这样一个问题:如果欧洲一体化趋势持续,股票市场间相关系数上升到99%,对整个金融市场影响如何?反之,如果脱欧浪潮兴起,欧盟瓦解,相关系数急剧下降,对金融市场与资产配置的影响又如何?由于此类事件以往历史上未曾发生过,用历史数据的方法来进行分析是行不通的,只能引入模拟的方法来进行情景分析。
实务中最常使用的模拟方法就是蒙特卡洛模拟。蒙特卡洛模拟的基本思想是:假设与资产组合相关的各风险因子服从特定的概率分布,根据这些假定的概率分布进行抽样。随后,依据抽样数据计算资产最终价值。反复重复上述步骤N次,可求得N个资产的最终价值,从而形成资产最终价值的概率分布。
例如,某基金经理现有1000万元资金,全部投资于上证50ETF。已知上证50ETF日收益率为r,一个交易日后资金的价值将变为多少?如果按照传统的方法解决这个问题,将根据历史数据估算出上证50ETF的日均收益率r0,以此数值带入1000(1+r),即可求得期望资金终值。然而,如果利用蒙特卡洛模拟法则有所不同,步骤如下:
- 蒙特卡洛模拟将假设收益率r服从某个特定的分布,比如正态分布;
- 随后,依据正态分布的概率分布,对r的可能取值进行抽样;
- 根据抽样数据计算出对应的资产终值1000(1+ri);
- 重复步骤1到步骤3共N次,当N足够大时就可以画出资产终值在各个区间内的直方图,并用计算机模拟出资产终值的概率分布。
通过上述步骤可以看出,蒙特卡洛模拟与传统方法的最大区别在于:传统模拟的方法只会计算出一个资产终值,而蒙特卡洛模拟可以计算出资产终值的概率分布。因此,在假定分布正确的情况下,蒙特卡洛模拟可以依据资产终值的概率分布进行情景分析。
蒙特卡洛模拟同样存在以下缺点。
- 蒙特卡洛模拟相当复杂,当模拟次数N非常大时,对计算机的性能要求也相当高。
- 蒙特卡洛模拟结论的准确性极其依赖于假设分布。如果对风险因子服从的分布假设不准确,则由蒙特卡洛模拟得出的结论也是不准确的。
历史法模拟
在蒙特卡洛模拟中,是由分析师决定风险因子的概率分布。历史法模拟则是根据实际历史数据来决定风险因子的概率分布。通过定义就可以看出,历史法模拟的准确性依赖于历史数据,其缺点如下所示:
- 历史法只能反映历史数据存在的风险,如果分析对象出现结构性改变,则历史法得出的结论就不准确;
- 历史法是基于已经发生的历史数据,因而无法进行情景分析。