1909 - 跳石头
题目描述
一年一度的“跳石头”比赛又要开始了!
这项比赛将在一条笔直的河道中进行,河道中分布着一些巨大岩石。组委会已经选择好了两块岩石作为比赛起点和终点。在起点和终点之间,有 N 块岩石(不含起点和终点的岩石)。在比赛过程中,选手们将从起点出发,每一步跳向相邻的岩石,直至到达终点。
为了提高比赛难度,组委会计划移走一些岩石,使得选手们在比赛过程中的最短跳跃距离尽可能长。由于预算限制,组委会至多从起点和终点之间移走 M 块岩石(不能移走起点和终点的岩石)。
输入
第一行包含三个整数 L,N,M ,分别表示起点到终点的距离,起点和终点之间的岩石数,以及组委会至多移走的岩石数。保证L≥1 且 N≥M≥0 。
接下来 N 行,每行一个整数,第 i 行的整数 Di( 0 < Di < L), 表示第 i 块岩石与起点的距离。这些岩石按与起点距离从小到大的顺序给出,且不会有两个岩石出现在同一个位置。
输出
一个整数,即最短跳跃距离的最大值。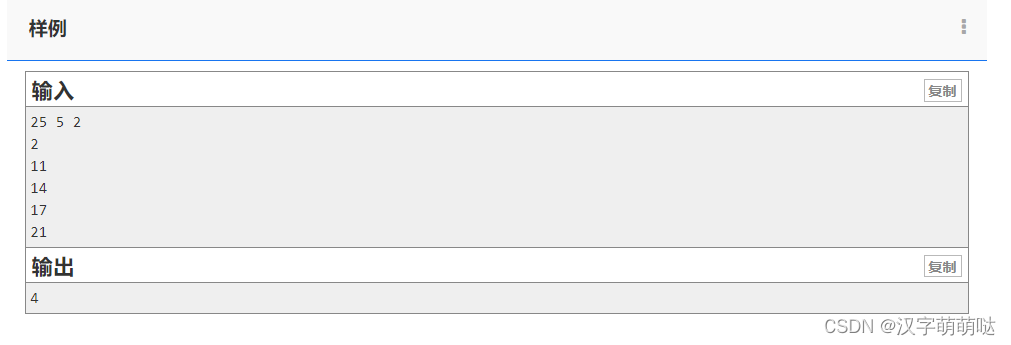

#include <bits/stdc++.h>
using namespace std;
/*c<=m说明最短跳跃距离太小,要放大
否则,缩小*/
const int N=50100;
int a[N];
int n,m,l;//l河道长度
bool check(int mid) {int c=0;//搬走的数量int p=0;//人的位置for(int i=1; i<=n; i++) {if(a[i]-p<mid) {c++;} else {p=a[i];}}if(l-p<mid) c++;return c<=m;
}
int main() {cin>>l>>n>>m;for(int i=1; i<=n; i++) {cin>>a[i];}int left=1,right=l,mid;while(left<=right) {mid=left+right>>1;//mid=(left+right)/2if(check(mid)) {left=mid+1;} else {right=mid-1;}}cout<<left-1;return 0;
}1908 - 伐木工
题目描述
伐木工人米尔科需要砍倒M米长的木材。这是一个对米尔科来说很容易的工作,因为他有一个漂亮的新伐木机,可以像野火一样砍倒森林。不过,米尔科只被允许砍倒单行树木。
米尔科的伐木机工作过程如下:米尔科设置一个高度参数H(米),伐木机升起一个巨大的锯片到高度H,并锯掉所有的树比H高的部分(当然,树木不高于H米的部分保持不变)。米尔科就得到树木被锯下的部分。
例如,如果一行树的高度分别为20,15,10和17,米尔科把锯片升到15米的高度,切割后树木剩下的高度将是15,15,10和15,而米尔科将从第1棵树得到5米,从第4棵树得到2米,共得到7米木材。
米尔科非常关注生态保护,所以他不会砍掉过多的木材。这正是他为什么尽可能高地设定伐木机锯片的原因。帮助米尔科找到伐木机锯片的最大的整数高度H,使得他能得到木材至少为M米。换句话说,如果再升高1米,则他将得不到M米木材。
输入
第1行:2个整数N和M,N表示树木的数量(1<=N<=106),M表示需要的木材总长度(1<=M<=2 * 109)
第2行:N个整数表示每棵树的高度,值均不超过109。所有木材长度之和大于M,因此必有解。
输出
1个整数,表示砍树的最高高度。
#include <bits/stdc++.h>
using namespace std;
const int N=1000010;
long long a[N];
long long n,m,l=1,r,mid;
bool check(long long x){long long s=0;for(int i=1;i<=n;i++){if(x<a[i]) s=s+a[i]-x;if(s>=m) return true;}return false;
}
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++){cin>>a[i];r=max(a[i],r);}
while(l<=r){mid=l+r>>1;if(check(mid)){l=mid+1;}else{r=mid-1;}
}
cout<<l-1;return 0;
}1898 - 同时出现的数
题目描述
MedusaMedusa 同学拿到了 22 组数字,老师请你编程帮他找出,第 22 组数中的哪些数,在第 11 组数中出现了,从小到大输出所有满足条件的数。
比如:
第 11 组数有:88 77 99 88 22 66 33
第2组数有:99 66 88 33 33 22 1010
那么应该输出:22 33 33 66 88 99
输入
第一行两个整数 nn 和 mm ,分别代表 22 组数的数量。
第二行 nn 个正整数。
第三行 mm 个正整数。
对于 60\%60% 的数据 1 \le n1≤n,m \le 1000m≤1000,每个数\le 2\times 10^9≤2×109。
对于 100\%100% 的数据 1 \le n1≤n, m \le 100000m≤100000 ,每个数 \le 2\times 10^9≤2×109。
输出
按照要求输出满足条件的数,数与数之间用空格隔开。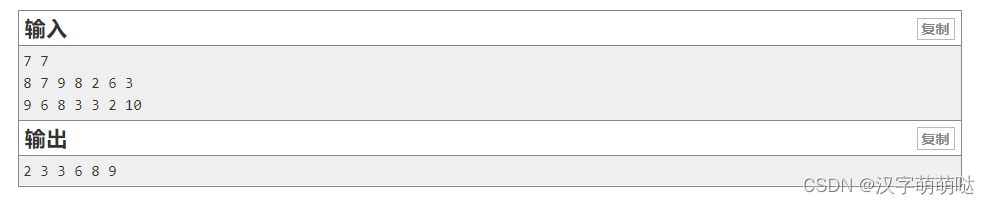
#include <bits/stdc++.h>
using namespace std;
int a[100010],b[100010];
int n,m;
bool find(int x) {int l=1,r=n,mid;while(l<=r) {mid=(l+r)/2;if(x>a[mid]) {l=mid+1;} else if(x<a[mid]) {r=mid-1;} else {return true;}}return false;
}
int main() {cin>>n>>m;for(int i=1; i<=n; i++) {cin>>a[i];}for(int i=1; i<=m; i++) {cin>>b[i];}sort(a+1,a+n+1); sort(b+1,b+m+1);for(int i=1; i<=m; i++) {if(find(b[i])==true) {cout<<b[i]<<" ";}}return 0;
}1899 - 最满意的方案
题目描述
高考结束了,同学们要开始了紧张的填写志愿的过程,大家希望找一个自己最满意的大学填报方案,请你编程帮忙实现。 现有 mm (m≤100000m≤100000) 所学校,每所学校预计分数线是 a_iai (a_i≤10^6ai≤106) 。有 nn(n≤100000n≤100000) 位学生,估分分别为 b_ibi (b_i≤10^6bi≤106)。
根据 nn 位学生的估分情况,分别给每位学生推荐一所学校,要求学校的预计分数线和学生的估分相差最小(可高可低,毕竟是估分嘛),这个最小值为不满意度。求所有学生不满意度和的最小值。
输入
第一行读入两个整数 m,nm,n,mm 表示学校数, nn 表示学生数。
第二行共有 mm 个数,表示 mm 个学校的预计录取分数。
第三行有 nn 个数,表示 nn 个学生的估分成绩。
输出
一行,为最小的不满意度之和。(数据保证计算结果≤10^9≤109)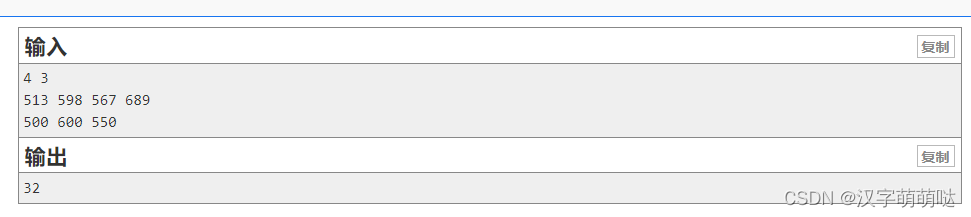
#include <bits/stdc++.h>
using namespace std;
const int N=100100;
int a[N],x;
int n,m,s=0;//最小差值的和
int main(){cin>>m>>n;for(int i=1;i<=m;i++){cin>>a[i];}sort(a+1,a+m+1);int l,r,mid;for(int i=1;i<=n;i++){cin>>x;if(x<=a[1]) s=s+a[1]-x;else if(x>=a[m]) s=s+x-a[m];else{l=1;r=m;while(l<=r){mid=(l+r)>>1;if(x<=a[mid]) r=mid-1;else l=mid+1;}s=s+min(a[l]-x,x-a[l-1]);}}
cout<<s;return 0;
}1916 - 防御迷阵
题目描述
一队士兵来到了敌军城外,准备进攻敌城。敌人在城外布置一个防御迷阵,要进入城池首先必须通过城池外的防御迷阵。
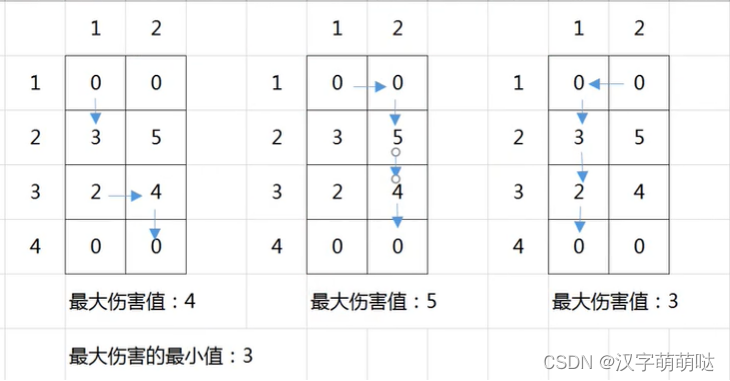
迷阵由 n \times mn×m 个相同的小房间组成,每个房间与相邻四个房间之间有门可通行。而第 11 行的 mm 个房间有 mm 扇向外打开的门,是迷阵的入口。除了第 11 行和第 nn 行的房间外,每个房间都安装了激光杀伤装置,将会对进入房间的人造成一定的伤害。第 ii 行第 jj 列造成的伤害值为aaijij。 (第 11 行和第 nn 行的 aaijij 值全部为0)。
现在士兵打算以最小伤害代价通过迷阵,显然,他们可以选择任意多的人从任意的门进入,但必须到达第 nn 行的房间。一个士兵受到的伤害值为他在经过的路径上所有房间的伤害值中的最大值。现在,士兵们掌握了迷阵的情况,他们需要提前知道怎么安排士兵的行进路线可以使得伤害值最小。
输入
第一行有两个整数 n,mn,m 表示迷阵的大小。
接下来 nn 行,每行 mm 个数,第 ii 行第 jj 列的数表示 a_{ij}aij 。
数据范围:2≤n,m≤10002≤n,m≤1000,1≤a1≤aijij≤1000≤1000。
输出
输出一个数,表示最小伤害代价。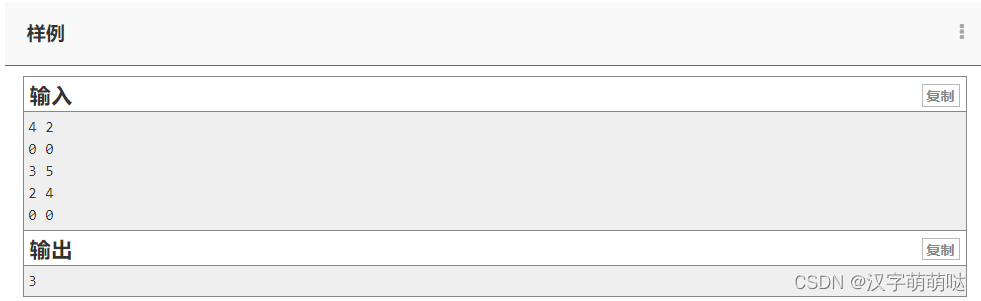
#include <bits/stdc++.h>
using namespace std;
int a[1010][1010];
int n,m;
int l=INT_MAX,r=INT_MIN,mid;
int q[1000100][3];
int fx[5]= {0,0,1,0,-1};
int fy[5]= {0,1,0,-1,0};
bool f[1010][1010];
bool check(int v) {memset(f,false,sizeof(f));int h=1,t=1;q[1][1]=1;q[1][2]=1;f[1][1]=true;int tx,ty;while(h<=t) {for(int i=1; i<=4; i++) {tx=q[h][1]+fx[i];ty=q[h][2]+fy[i];if(tx>=1&&tx<=n&&ty>=1&&ty<=m&&!f[tx][ty]&&a[tx][ty]<=v) {t++;q[t][1]=tx;q[t][2]=ty;f[tx][ty]=true;if(tx==n) return true;}}h++;}return false;
}
int main() {cin>>n>>m;for(int i=1; i<=n; i++) {for(int j=1; j<=m; j++) {cin>>a[i][j];if(i!=1&&i!=n) {l=min(l,a[i][j]);r=max(r,a[i][j]);}}}while(l<=r) {mid=l+r>>1;if(check(mid)) {r=mid-1;} else {l=mid+1;}}cout<<l;return 0;
}1895 - 二分查找右侧边界
题目描述
请在一个有序不递减的数组中(数组中的值有相等的值),采用二分查找,找到最后 11 次出现值 xx 的位置,如果不存在 xx 请输出 -1−1。
请注意:本题要求出 qq 个 xx,每个 xx 在数组中最后一次出现的位置。
比如有 66 个数,分别是:11 22 22 22 33 33,那么如果要求 33 个数:33 22 55,在数组中最后一次出现的位置,答案是:66 44 -1−1。
输入
第一行,一个整数 nn,代表数组元素个数(n \le 10^5n≤105)
第二行,nn 个整数,用空格隔开,代表数组的 nn 个元素(1 \le1≤数组元素的值\le 10^8≤108)
第三行,一个整数 qq ,代表有要求出 qq 个数最后一次出现的位置(q \le 10^5q≤105)
第四行,qq 个整数,用空格隔开,代表要找的数(1 \le1≤要找的数\le 10^8≤108)
输出
按题意输出位置或者 -1−1。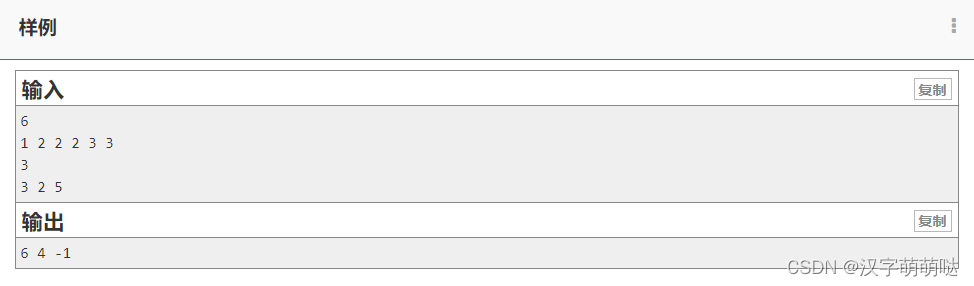
#include <bits/stdc++.h>
using namespace std;
const int N =100100;
int a[N];
int n,q;//q次查询
int fun(int x) {int l=1,r=n,mid;while(l<=r) {mid=(l+r)>>1;if(x<a[mid]) {r=mid-1;} else if(x>a[mid]) {l=mid+1;} else if(x==a[mid]) {l=mid+1;}}if(a[l-1]==x) {return l-1;} else {return -1;}}
int main() {cin>>n;for(int i=1; i<=n; i++) {cin>>a[i];}cin>>q;int x;
//q次查询for(int i=1; i<=q; i++) {cin>>x;cout<<fun(x)<<" ";}return 0;
}



![【Hadoop】-Apache Hive使用语法与概念原理[15]](https://img-blog.csdnimg.cn/direct/493b098a7ea94176ae87e70de30a1aca.png)