C++中的数据结构与算法

在这里插入图片描述

随处可见的红黑树

一般会用到[key,value]。
例如github中这个例子，第一个是访问网站，第二个是访问次数，但是这个不是静态的，这有个动态排序，并且当我们需要让相应的访问次数加1的时候，我们用红黑树查找的时候会比较快，所以用红黑树表示这个结构比较号。
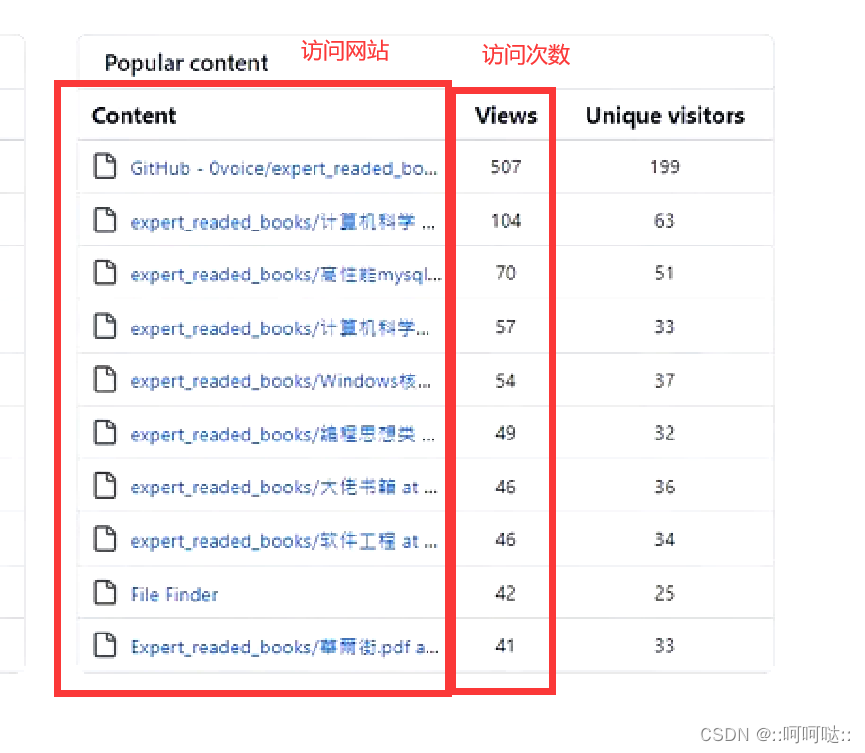
在这里插入图片描述
所以红黑树普遍用于强查找过程。对于这种强查找的过程：我们普遍用rbtree，hash，b/b+ tree，或者跳表。

红黑树的性质和定义

红黑树的性质：
1.每个结点是红的或者黑的2.根结点是黑的
3.每个叶子结点是黑的
4.如果一个结点是红的，则它的两个儿子都是黑的(红红不相邻)
5.对每个结点，从该结点到其子孙结点的所有路径上的包含相同数目的黑结点
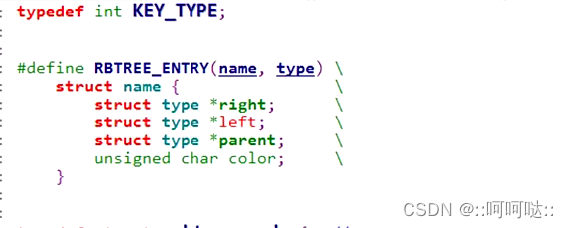
在这里插入图片描述

在这里插入图片描述在这里插入图片描述
对于一个红黑树的定义：注意这个nil指的是叶子节点，也就是那个隐藏的那个黑节点。

typedef int KEY_TYPE;typedef struct _rbtree_node {unsigned char color;struct _rbtree_node *right;struct _rbtree_node *left;struct _rbtree_node *parent;KEY_TYPE key;void *value;
} rbtree_node;typedef struct _rbtree {rbtree_node *root;//根节点rbtree_node *nil;//叶子节点
} rbtree;

红黑树的左右旋

对于红黑树的旋转：
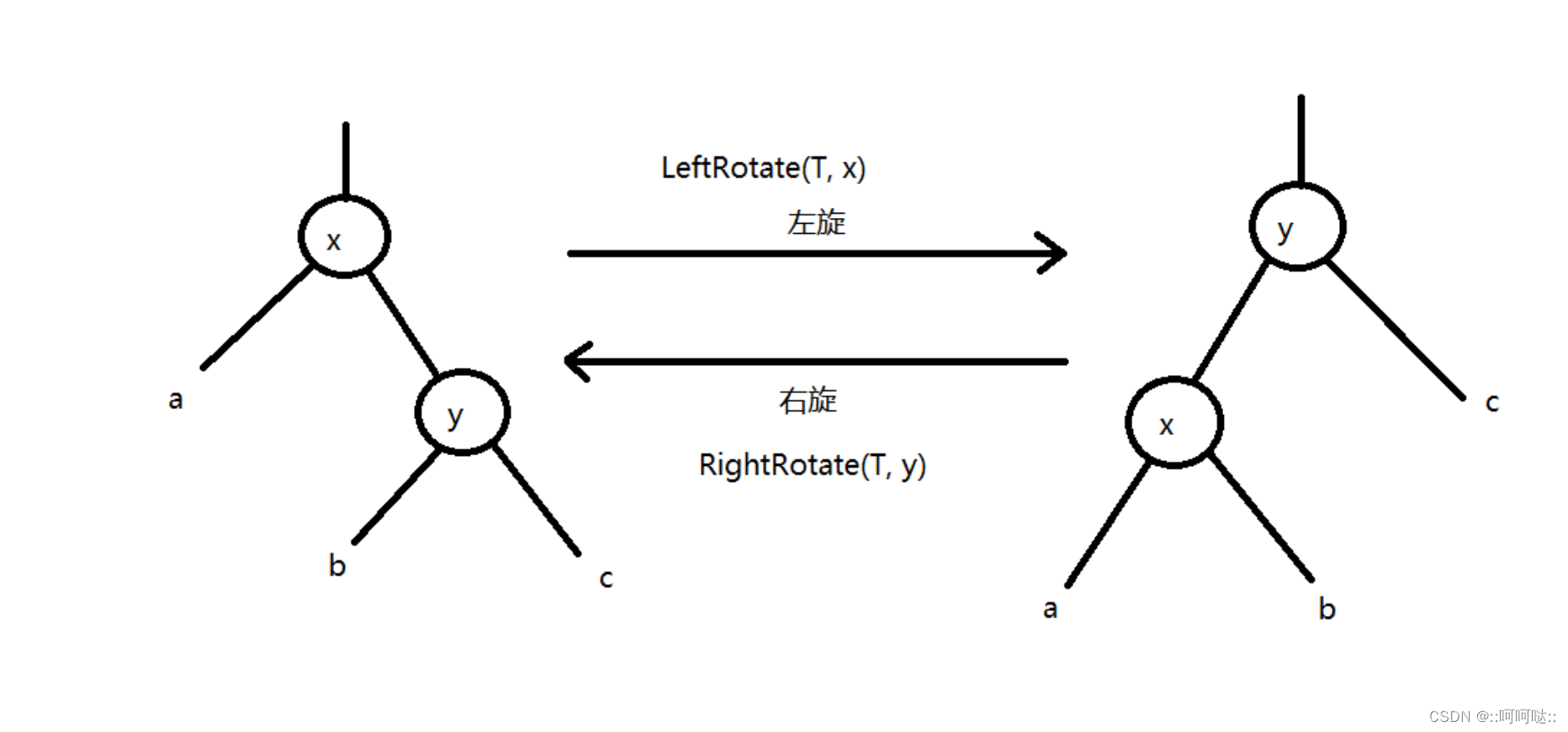
在这里插入图片描述
这里我们需要改变6根指针：
code:
这里主要需要判断的是x的parent是不是根节点。如果是的话，那么之间让根节点root指向y就行。
在这里插入图片描述

void rbtree_left_rotate(rbtree *T, rbtree_node *x) {rbtree_node *y = x->right;  // x  --> y  ,  y --> x,   right --> left,  left --> rightx->right = y->left; //1 1if (y->left != T->nil) { //1 2y->left->parent = x;}y->parent = x->parent; //1 3if (x->parent == T->nil) { //1 4T->root = y;} else if (x == x->parent->left) {x->parent->left = y;} else {x->parent->right = y;}y->left = x; //1 5x->parent = y; //1 6
}

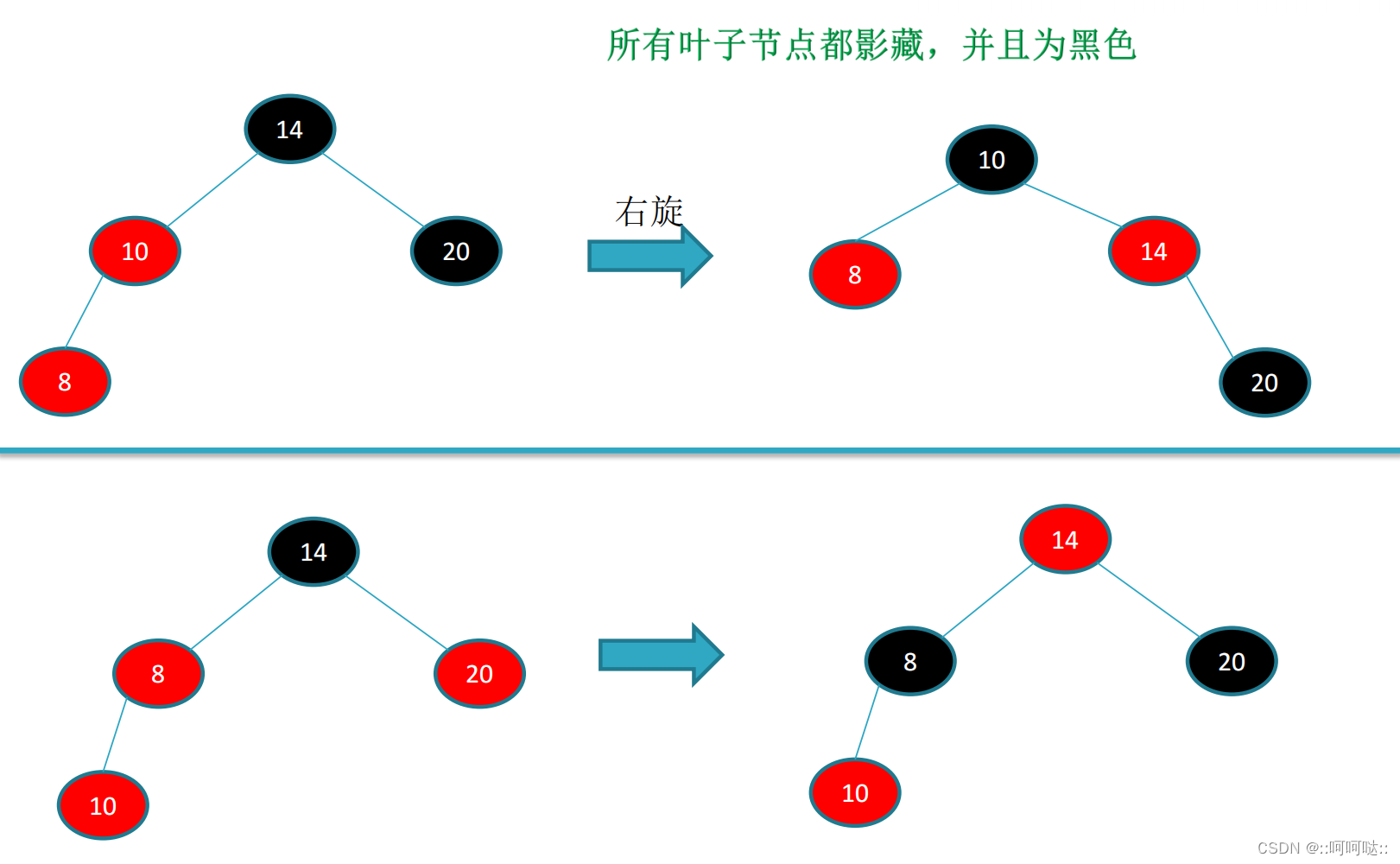
右旋：
也就是上面的代码x改成y,right改成left。

void rbtree_right_rotate(rbtree *T, rbtree_node *y) {rbtree_node *x = y->left;y->left = x->right;if (x->right != T->nil) {x->right->parent = y;}x->parent = y->parent;if (y->parent == T->nil) {T->root = x;} else if (y == y->parent->right) {y->parent->right = x;} else {y->parent->left = x;}x->right = y;y->parent = x;
}

在这里插入图片描述

红黑树的插入

对于插入的时候我们都是一插到底，一直插到根节点。并且插入的节点定义为红色，然后再进行颜色的调整。而且它的父节点也是红色，因为原本的节点他的两个根是黑色，所以，这个父节点应该是红色。
因为红黑树在插入节点之前他已经是一个红黑树了。所以插入红色，不改变黑高的性质。
插入code:

void rbtree_insert(rbtree *T, rbtree_node *z) {rbtree_node *y = T->nil;rbtree_node *x = T->root;while (x != T->nil) {y = x;//y就是x的parentif (z->key < x->key) {x = x->left;} else if (z->key > x->key) {x = x->right;} else { //Existreturn ;}}z->parent = y;if (y == T->nil) {T->root = z;} else if (z->key < y->key) {y->left = z;} else {y->right = z;}z->left = T->nil;z->right = T->nil;z->color = RED;rbtree_insert_fixup(T, z);
}

调整颜色，让其满足性质：

我们发现如果定义为红色之后，满足性质1，2，3。不知道满不满足4，5.所以我们要让其先满足5在满足4。
还没调整前的情况：假设插入的节点是z，z的父节点是y

z是红色
z的父节点y也是红色
z的祖父节点是黑色
z的叔父节点是不确定

那么就两种情况：

  1. z的叔父节点是红色
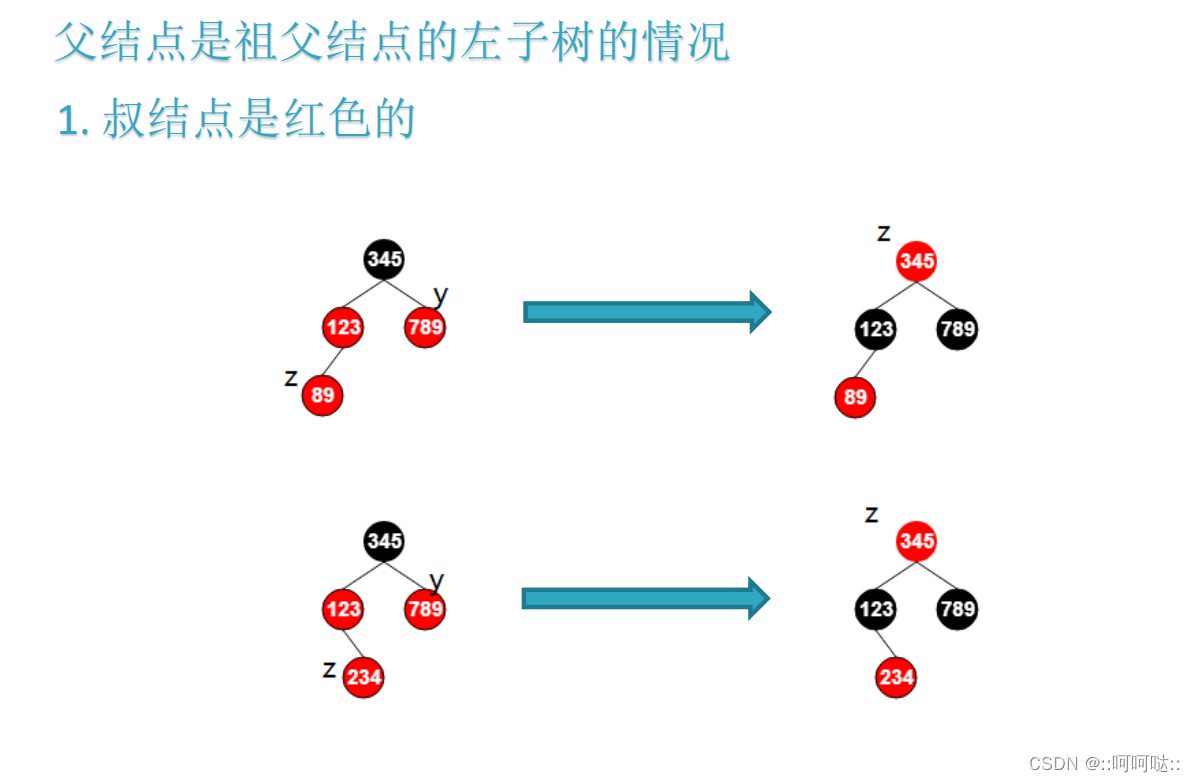
    在这里插入图片描述
z->parent->color = BLACK;
y->color = BLACK;
z->parent->parent->color = RED;
z = z->parent->parent; //z --> RED,需要回溯
  1. z的叔父节点是黑色
    这两种情况是调整出来的，因为你调整完之后需要回溯，因为你调整完之后它的祖父可能不满足所以z = z->parent->parent。然后这种情况是要旋转的。然后旋转之后的图是中间状态的图，然后旋转完之后就是改色。
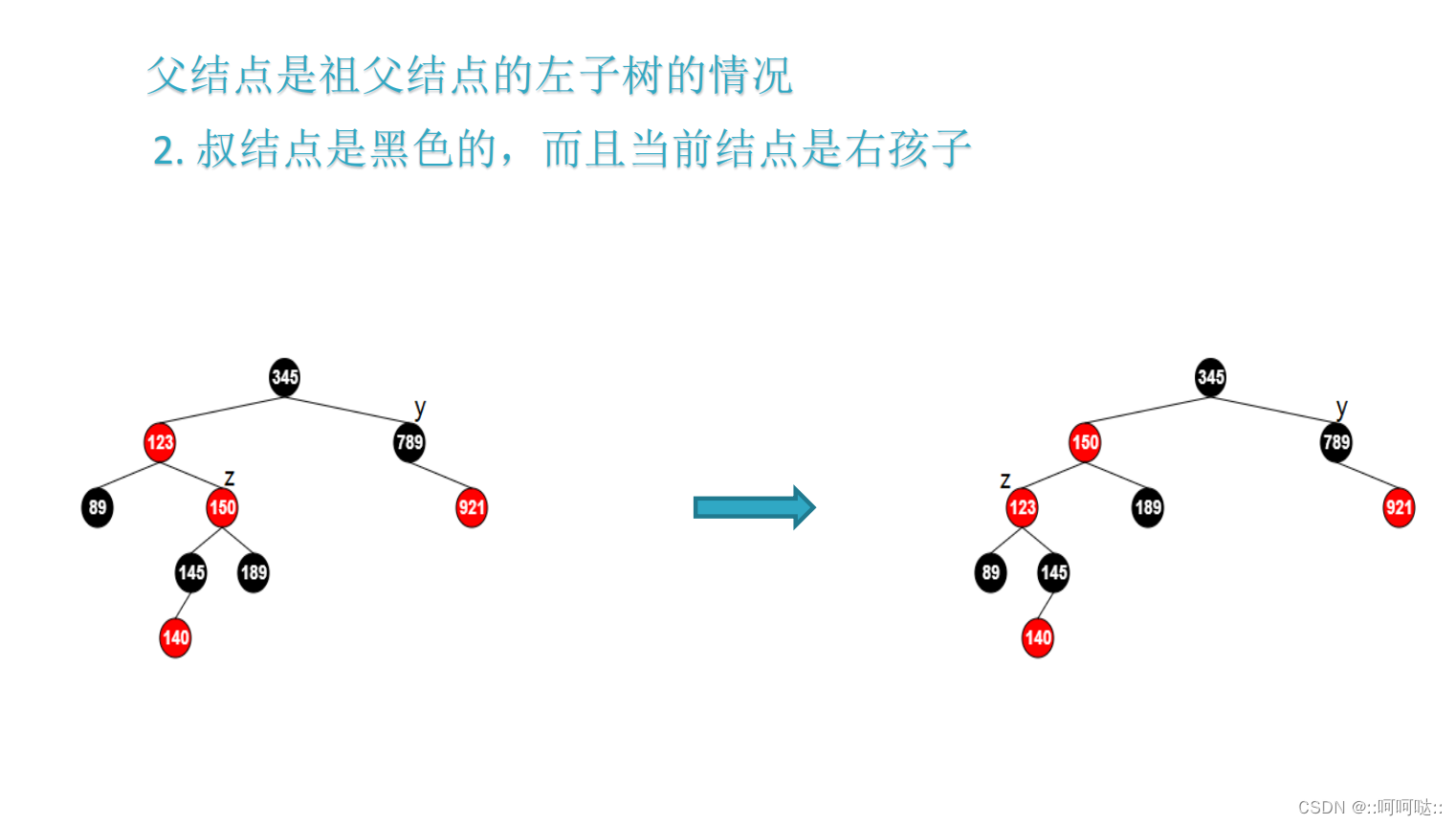
    在这里插入图片描述
if (z == z->parent->right) {z = z->parent;rbtree_left_rotate(T, z);
}

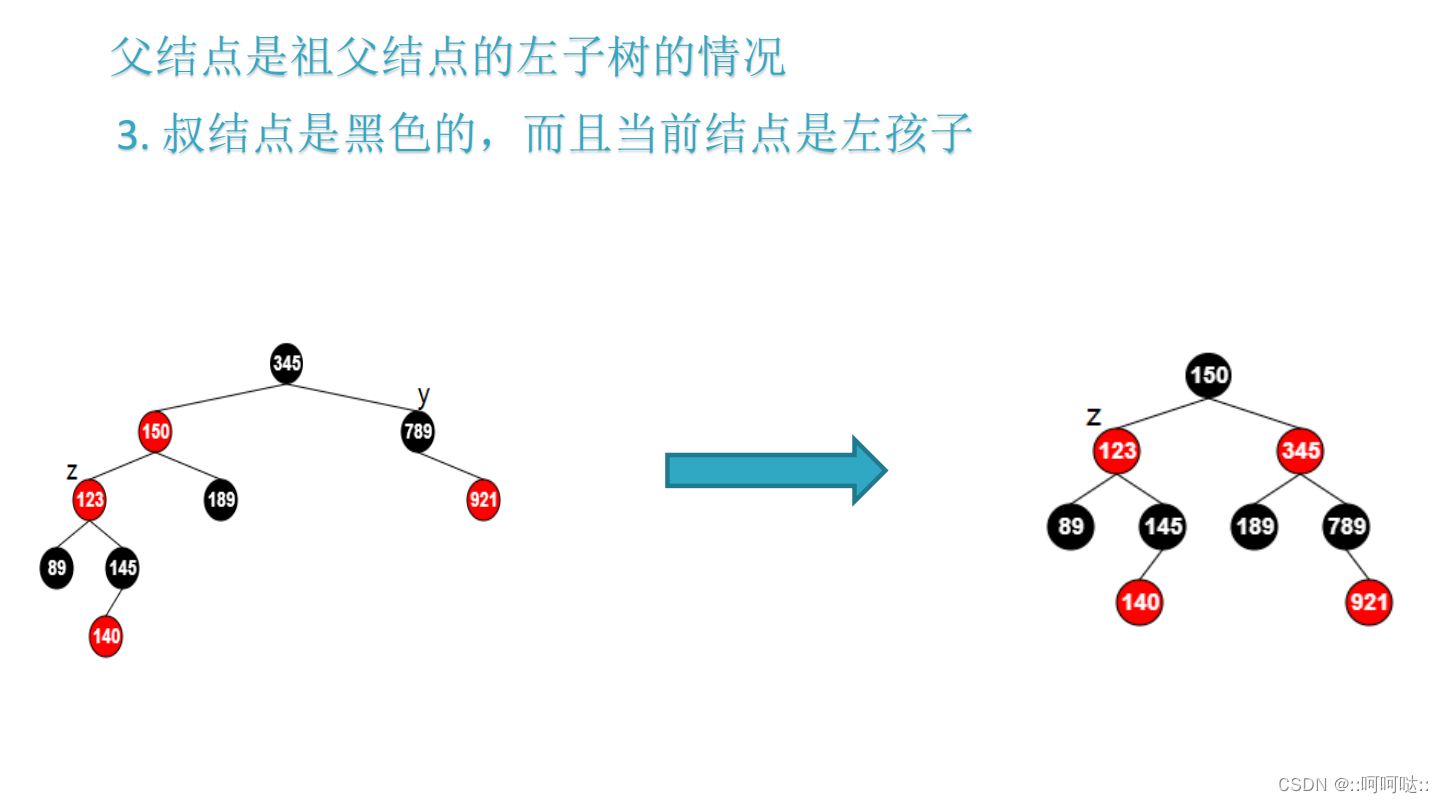
在这里插入图片描述

z->parent->color = BLACK;
z->parent->parent->color = RED;
rbtree_right_rotate(T, z->parent->parent);

然后叔父节点是黑色的完整代码就是这个：

if (z == z->parent->right) {z = z->parent;rbtree_left_rotate(T, z);
}z->parent->color = BLACK;
z->parent->parent->color = RED;
rbtree_right_rotate(T, z->parent->parent);

然后父节点是祖父节点的左子树的情况代码就是这样的：

if (z->parent == z->parent->parent->left) {rbtree_node *y = z->parent->parent->right;if (y->color == RED) {z->parent->color = BLACK;y->color = BLACK;z->parent->parent->color = RED;z = z->parent->parent; //z --> RED,需要回溯} else {if (z == z->parent->right) {z = z->parent;rbtree_left_rotate(T, z);}z->parent->color = BLACK;z->parent->parent->color = RED;rbtree_right_rotate(T, z->parent->parent);}
}

然后父节点是祖父节点的右子树的情况和上面差不多
完整代码就是：

void rbtree_insert_fixup(rbtree *T, rbtree_node *z) {while (z->parent->color == RED) { //z ---> REDif (z->parent == z->parent->parent->left) {rbtree_node *y = z->parent->parent->right;if (y->color == RED) {z->parent->color = BLACK;y->color = BLACK;z->parent->parent->color = RED;z = z->parent->parent; //z --> RED,需要回溯} else {if (z == z->parent->right) {z = z->parent;rbtree_left_rotate(T, z);}z->parent->color = BLACK;z->parent->parent->color = RED;rbtree_right_rotate(T, z->parent->parent);}}else {rbtree_node *y = z->parent->parent->left;if (y->color == RED) {z->parent->color = BLACK;y->color = BLACK;z->parent->parent->color = RED;z = z->parent->parent; //z --> RED} else {if (z == z->parent->left) {z = z->parent;rbtree_right_rotate(T, z);}z->parent->color = BLACK;z->parent->parent->color = RED;rbtree_left_rotate(T, z->parent->parent);}}}T->root->color = BLACK;
}

红黑树的删除

这个比较难，不需要掌握
完整代码：

#include <stdio.h>
#include <stdlib.h>
#include <string.h>#define RED				1
#define BLACK 			2typedef int KEY_TYPE;typedef struct _rbtree_node {unsigned char color;struct _rbtree_node *right;struct _rbtree_node *left;struct _rbtree_node *parent;KEY_TYPE key;void *value;
} rbtree_node;typedef struct _rbtree {rbtree_node *root;rbtree_node *nil;
} rbtree;rbtree_node *rbtree_mini(rbtree *T, rbtree_node *x) {while (x->left != T->nil) {x = x->left;}return x;
}rbtree_node *rbtree_maxi(rbtree *T, rbtree_node *x) {while (x->right != T->nil) {x = x->right;}return x;
}rbtree_node *rbtree_successor(rbtree *T, rbtree_node *x) {rbtree_node *y = x->parent;if (x->right != T->nil) {return rbtree_mini(T, x->right);}while ((y != T->nil) && (x == y->right)) {x = y;y = y->parent;}return y;
}void rbtree_left_rotate(rbtree *T, rbtree_node *x) {rbtree_node *y = x->right;  // x  --> y  ,  y --> x,   right --> left,  left --> rightx->right = y->left; //1 1if (y->left != T->nil) { //1 2y->left->parent = x;}y->parent = x->parent; //1 3if (x->parent == T->nil) { //1 4T->root = y;} else if (x == x->parent->left) {x->parent->left = y;} else {x->parent->right = y;}y->left = x; //1 5x->parent = y; //1 6
}void rbtree_right_rotate(rbtree *T, rbtree_node *y) {rbtree_node *x = y->left;y->left = x->right;if (x->right != T->nil) {x->right->parent = y;}x->parent = y->parent;if (y->parent == T->nil) {T->root = x;} else if (y == y->parent->right) {y->parent->right = x;} else {y->parent->left = x;}x->right = y;y->parent = x;
}void rbtree_insert_fixup(rbtree *T, rbtree_node *z) {while (z->parent->color == RED) { //z ---> REDif (z->parent == z->parent->parent->left) {rbtree_node *y = z->parent->parent->right;if (y->color == RED) {z->parent->color = BLACK;y->color = BLACK;z->parent->parent->color = RED;z = z->parent->parent; //z --> RED,需要回溯} else {if (z == z->parent->right) {z = z->parent;rbtree_left_rotate(T, z);}z->parent->color = BLACK;z->parent->parent->color = RED;rbtree_right_rotate(T, z->parent->parent);}}else {rbtree_node *y = z->parent->parent->left;if (y->color == RED) {z->parent->color = BLACK;y->color = BLACK;z->parent->parent->color = RED;z = z->parent->parent; //z --> RED} else {if (z == z->parent->left) {z = z->parent;rbtree_right_rotate(T, z);}z->parent->color = BLACK;z->parent->parent->color = RED;rbtree_left_rotate(T, z->parent->parent);}}}T->root->color = BLACK;
}void rbtree_insert(rbtree *T, rbtree_node *z) {rbtree_node *y = T->nil;rbtree_node *x = T->root;while (x != T->nil) {y = x;//y就是x的parentif (z->key < x->key) {x = x->left;} else if (z->key > x->key) {x = x->right;} else { //Existreturn ;}}z->parent = y;if (y == T->nil) {T->root = z;} else if (z->key < y->key) {y->left = z;} else {y->right = z;}z->left = T->nil;z->right = T->nil;z->color = RED;rbtree_insert_fixup(T, z);
}void rbtree_delete_fixup(rbtree *T, rbtree_node *x) {while ((x != T->root) && (x->color == BLACK)) {if (x == x->parent->left) {rbtree_node *w= x->parent->right;if (w->color == RED) {w->color = BLACK;x->parent->color = RED;rbtree_left_rotate(T, x->parent);w = x->parent->right;}if ((w->left->color == BLACK) && (w->right->color == BLACK)) {w->color = RED;x = x->parent;} else {if (w->right->color == BLACK) {w->left->color = BLACK;w->color = RED;rbtree_right_rotate(T, w);w = x->parent->right;}w->color = x->parent->color;x->parent->color = BLACK;w->right->color = BLACK;rbtree_left_rotate(T, x->parent);x = T->root;}} else {rbtree_node *w = x->parent->left;if (w->color == RED) {w->color = BLACK;x->parent->color = RED;rbtree_right_rotate(T, x->parent);w = x->parent->left;}if ((w->left->color == BLACK) && (w->right->color == BLACK)) {w->color = RED;x = x->parent;} else {if (w->left->color == BLACK) {w->right->color = BLACK;w->color = RED;rbtree_left_rotate(T, w);w = x->parent->left;}w->color = x->parent->color;x->parent->color = BLACK;w->left->color = BLACK;rbtree_right_rotate(T, x->parent);x = T->root;}}}x->color = BLACK;
}rbtree_node *rbtree_delete(rbtree *T, rbtree_node *z) {rbtree_node *y = T->nil;rbtree_node *x = T->nil;if ((z->left == T->nil) || (z->right == T->nil)) {y = z;} else {y = rbtree_successor(T, z);}if (y->left != T->nil) {x = y->left;} else if (y->right != T->nil) {x = y->right;}x->parent = y->parent;if (y->parent == T->nil) {T->root = x;} else if (y == y->parent->left) {y->parent->left = x;} else {y->parent->right = x;}if (y != z) {z->key = y->key;z->value = y->value;}if (y->color == BLACK) {rbtree_delete_fixup(T, x);}return y;
}rbtree_node *rbtree_search(rbtree *T, KEY_TYPE key) {rbtree_node *node = T->root;while (node != T->nil) {if (key < node->key) {node = node->left;} else if (key > node->key) {node = node->right;} else {return node;}	}return T->nil;
}void rbtree_traversal(rbtree *T, rbtree_node *node) {if (node != T->nil) {rbtree_traversal(T, node->left);printf("key:%d, color:%d\n", node->key, node->color);rbtree_traversal(T, node->right);}
}int main() {int keyArray[20] = {24,25,13,35,23, 26,67,47,38,98, 20,19,17,49,12, 21,9,18,14,15};rbtree *T = (rbtree *)malloc(sizeof(rbtree));if (T == NULL) {printf("malloc failed\n");return -1;}T->nil = (rbtree_node*)malloc(sizeof(rbtree_node));T->nil->color = BLACK;T->root = T->nil;rbtree_node *node = T->nil;int i = 0;for (i = 0;i < 20;i ++) {node = (rbtree_node*)malloc(sizeof(rbtree_node));node->key = keyArray[i];node->value = NULL;rbtree_insert(T, node);}rbtree_traversal(T, T->root);printf("----------------------------------------\n");for (i = 0;i < 20;i ++) {rbtree_node *node = rbtree_search(T, keyArray[i]);rbtree_node *cur = rbtree_delete(T, node);free(cur);rbtree_traversal(T, T->root);printf("----------------------------------------\n");}}

b/b+树

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.rhkb.cn/news/315833.html

如若内容造成侵权/违法违规/事实不符，请联系长河编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

C++每日一练——杨辉三角

C++每日一练——杨辉三角

给定一个非负整数 numRows&#xff0c;生成「杨辉三角」的前 numRows 行。 在「杨辉三角」中&#xff0c;每个数是它左上方和右上方的数的和。 示例 1: 输入: numRows 5 输出: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]示例 2: 输入: numRows 1 输出: [[1]]提示: 1 <…
阅读更多...
Jsoncpp搭建交叉编译环境（移植到arm）

Jsoncpp搭建交叉编译环境（移植到arm）

1. 官网下载源码 github地址&#xff1a;GitHub - open-source-parsers/jsoncpp at update 2. 交叉编译环境 当前平台/开发平台-编译环境&#xff1a; [rootlocalroot ~]# cat /etc/redhat-release CentOS Linux release 7.9.2009 (Core) [rootlocalroot ~]# uname -a Lin…
阅读更多...
ELK创建仪表盘

ELK创建仪表盘

创建仪表盘步骤&#xff1a; 一、保存search二、生成饼图三、创建仪表盘 一、保存search 首先保存一段时间内的search&#xff0c;可以添加想要的字段&#xff0c;并保存这个search方便下次直接打开该search&#xff0c;并方便在可视化和仪表盘中使用该search. 二、生成饼图…
阅读更多...
Mac安装telnet

Mac安装telnet

一、安装Homebrew 1、打开官网&#xff1a;Homebrew — The Missing Package Manager for macOS (or Linux) 2、打开终端输入&#xff1a; /usr/bin/ruby -e "$(curl -fsSL https://raw.githubusercontent.com/Homebrew/install/master/install)" 二、安装Telnet bre…
阅读更多...
数字文旅重塑旅游发展新格局：以数字化转型为突破口，提升旅游服务的智能化水平，为游客带来全新的旅游体验

数字文旅重塑旅游发展新格局：以数字化转型为突破口，提升旅游服务的智能化水平，为游客带来全新的旅游体验

随着信息技术的迅猛发展&#xff0c;数字化已成为推动各行各业创新发展的重要力量。在旅游业领域&#xff0c;数字文旅的兴起正以其强大的驱动力&#xff0c;重塑旅游发展的新格局。数字文旅以数字化转型为突破口&#xff0c;通过提升旅游服务的智能化水平&#xff0c;为游客带…
阅读更多...
急急急！微信朋友圈删除了怎么恢复？

急急急！微信朋友圈删除了怎么恢复？

微信朋友圈是我们与朋友分享生活点滴的重要平台&#xff0c;但有时候微信出现异常&#xff0c;导致我们编辑好的朋友圈被删除了&#xff0c;这时候该怎么办呢&#xff1f; 幸运的是&#xff0c;微信提供了一种简单的方式来恢复已删除的朋友圈内容。微信朋友圈删除了怎么恢复&a…
阅读更多...
四信数字孪生水库解决方案，加快构建现代化水库运行管理矩阵

四信数字孪生水库解决方案，加快构建现代化水库运行管理矩阵

近年&#xff0c;水利部先后出台《关于加快构建现代化水库运行管理矩阵的指导意见》与《构建现代化水库运行管理矩阵先行先试工作方案》等文件&#xff0c;明确总体要求及试点水库、先行区域建设技术要求等&#xff0c;为全面推进现代化水库运行管理矩阵建设工作提供依据。 《2…
阅读更多...
【Elasticsearch＜一＞✈️✈️】简单安装使用以及各种踩坑

【Elasticsearch＜一＞✈️✈️】简单安装使用以及各种踩坑

目录 &#x1f378;前言 &#x1f37b;一、软件安装&#xff08;Windows版&#xff09; 1.1、Elasticsearch 下载 2.1 安装浏览器插件 3.1、安装可视化工具 Kibana 4.1、集成 IK 分词器 &#x1f37a;二、安装问题 &#x1f379;三、测试 IK 分词器 ​&#x1f377; 四、章…
阅读更多...
spi接口的基本概念、引脚定义及注意事项

spi接口的基本概念、引脚定义及注意事项

目录 基本概念 引脚定义 注意事项 SPI&#xff08;Serial Peripheral Interface&#xff09;是一种同步串行接口技术&#xff0c;广泛应用于微控制器和各种外围设备之间的短距离通信。 基本概念 SPI接口允许微控制器以串行方式与一个或多个外围设备进行通信。它是一种高速、…
阅读更多...
统信UOS下如何配置全局搜索

统信UOS下如何配置全局搜索

原文链接&#xff1a;统信UOS下如何配置全局搜索 Hello&#xff0c;大家好啊&#xff01;全局搜索是操作系统中非常实用的一个功能&#xff0c;它可以帮助我们快速定位文件、程序和其他资源。今天&#xff0c;我要给大家介绍如何在统信UOS桌面操作系统上配置全局搜索&#xff0…
阅读更多...
IT廉连看——UniApp——样式绑定

IT廉连看——UniApp——样式绑定

IT廉连看——UniApp——样式绑定 一、样式绑定 两种添加样式的方法&#xff1a; 1、第一种写法 写一个class属性&#xff0c;然后将css样式写在style中。 2、第二种写法 直接把style写在class后面 添加一些效果&#xff1a;字体大小 查看效果 证明这样添加样式是没有问题的…
阅读更多...
基于阶梯碳交易的含P2G-CCS耦合和燃气掺氢的虚拟电厂优化调度（matlab代码）

基于阶梯碳交易的含P2G-CCS耦合和燃气掺氢的虚拟电厂优化调度（matlab代码）

目录 1 主要内容 系统结构图 P2G-CCS 耦合模型 系统掺氢分析 其他算例对比 2 部分代码 3 下载链接 1 主要内容 该程序复现《基于阶梯碳交易的含P2G-CCS耦合和燃气掺氢的虚拟电厂优化调度》模型&#xff0c;以碳交易和碳封存成本、燃煤机组启停和煤耗成本、弃风成本、购…
阅读更多...
数据结构-二叉搜索树(BST)

数据结构-二叉搜索树(BST)

目录 什么是二叉搜索树 二叉搜索树的特性 (1)顺序性 (2)局限性 二叉搜索树的应用 二叉搜索树的操作 (1)查找节点 (2)插入节点 (3)删除节点 (4)中序遍历 什么是二叉搜索树 如图所示&#xff0c;二叉搜索树&#xff08;binary search tree&#xff09;满足以下条件。…
阅读更多...
2024长三角快递物流展：科技激荡，行业焕发新活力

2024长三角快递物流展：科技激荡，行业焕发新活力

7月8日&#xff0c;杭州将迎来快递物流科技盛宴&#xff0c;这是一年一度的行业盛会&#xff0c;吸引了全球领先的快递物流企业和创新技术汇聚一堂。届时&#xff0c;会展中心将全方位展示快递物流及供应链、分拣系统、输送设备、智能搬运、智能仓储、自动识别、无人车、AGV机器…
阅读更多...
【树莓派】yolov5 Lite，目标检测，行人检测入侵报警，摄像头绑定

【树莓派】yolov5 Lite，目标检测，行人检测入侵报警，摄像头绑定

延续之前的程序&#xff1a; https://qq742971636.blog.csdn.net/article/details/138172400 文章目录 播放声音pygame不出声音怎么办&#xff08;调节音量&#xff09;树莓派上的音乐播放器&#xff08;可选&#xff09;命令行直接放歌&#xff08;尝试放mp3歌曲&#xff09; …
阅读更多...
深度学习的炼金术：转化数据为黄金的秘密

深度学习的炼金术：转化数据为黄金的秘密

深度学习的炼金术&#xff1a;转化数据为黄金的秘密 1 引言 在现代深度学习的壮阔疆域中&#xff0c;数据是王冠上耀眼的宝石&#xff0c;而性能优化则是锻造这顶王冠的炼金术。这份融合了数据和算法魔力的艺术&#xff0c;不仅仅依赖于强大的计算资源和复杂的网络结构&#x…
阅读更多...
Docker——开源的应用容器的引擎

Docker——开源的应用容器的引擎

目录 一、前言 1.虚拟化产品有哪些 1.1寄居架构 1.2源生架构 2.虚拟化产品对比/介绍 2.1虚拟化产品 2.1.1仿真虚拟化 2.1.2半虚拟化 2.1.3全虚拟化 2.2重点 2.2.1KVM——Linux内核来完成的功能和性能 2.2.2ESXI——用的比较多 二、Docker概述 1.Docker定义 2.Do…
阅读更多...
常用算法代码模板 (3) ：搜索与图论

常用算法代码模板 (3) ：搜索与图论

AcWing算法基础课笔记与常用算法模板 (3) ——搜索与图论 常用算法代码模板 (1) &#xff1a;基础算法 常用算法代码模板 (2) &#xff1a;数据结构 常用算法代码模板 (3) &#xff1a;搜索与图论 常用算法代码模板 (4) &#xff1a;数学知识 文章目录 0 搜索技巧1 树与图的存…
阅读更多...
【while循环】

【while循环】

目录 什么是循环 while语句的执行过程 编程求1*2*3*...*n 所有不超过1000的数中含有数字3的自然数 求数 求数II 编程求1平方2平方...n平方 什么是循环 循环就是重复做同样的事儿使用while语句循环输出1到100 int i 1; while( i < 100 ){cout <<…
阅读更多...
Java虚拟机垃圾收集器详细总结

Java虚拟机垃圾收集器详细总结

1、Serial收集器 Serial收集器是最基础、历史最悠久的收集器&#xff0c;曾经&#xff08;在JDK 1.3.1之前&#xff09;是HotSpot虚拟机新生代收集器的唯一选择。这个收集器是一个单线程工作的收集器&#xff0c;但它的“单线 程”的意义并不仅仅是说明它只会使用一个处理器或一…
阅读更多...
最新文章
推荐文章

Copyright @ 2022~2023