针孔相机模型原理坐标系辨析内参标定流程内参变换

针孔相机的内参标定

针孔相机原理
- 真空相机模型
- 图片的伸缩和裁剪变换
内参标定———非线性优化
张正定标定详细原理(含公式推导)
通过多张棋盘格照片完成相机的内参标定流程(C++代码)
其他工具箱

相机分为短焦镜头和长焦镜头，短焦镜头看到的视野更广阔，同样距离大小的一颗树，在短焦相机中所占的像素个数较少。
长焦镜头看到的视野较窄，能看的更远。因为同样距离大小的一棵树，在长焦距镜头中的像素个数更多；
同一款芯片，短焦距fov大，长焦fov小。

针孔相机原理

真空相机模型

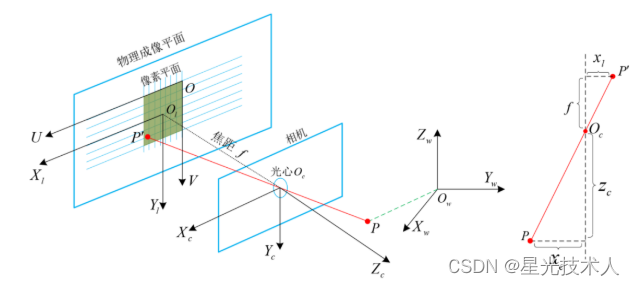
要搞明白针孔相机模型，首先需要明确世界坐标系 $OX_wY_wZ_w$ 、相机坐标系 $OX_cY_cZ_c$ 、物理坐标系 $OX_lY_l$ 和像素坐标系 $O U V$ 之间的关系。最重要的是需要理解物理坐标系和像素坐标系之间的变换关系。
在这里插入图片描述

坐标系之间的关系
- 这里提到的世界坐标系，只是一种表征的方式，与其他专业领域提到的世界坐标系不一样。这里仅仅指代的是某个自定义原定的坐标系。在自动驾驶的传感器标定中，多指车体坐标系和激光雷达坐标系。尺度为m
- 相机坐标系。相机坐标系是以相机光心为原点的笛卡尔坐标系，遵循右手定则。正前方深度方向为Z轴，y轴方向根据相机安装方式可以朝上也可以朝下，x轴方向取决于y轴的方向(根据右手定则确定)。尺度为m
- 物理坐标系。物理坐标系与图像采集传感器联系紧密。也就是说光线在感光芯片上的成像点。原点通常情况下是成像平面的中心。以索尼IMX249芯片为例，芯片尺寸为 $11.33mm \times 7.13mm$ 。那么 $x_l \in [-5.665mm, 5.665mm], y \in [-3.565mm, 3.565mm]$ 。
- 像素坐标系。像素坐标系与芯片的像素尺寸 $\sigma_u, \sigma_v$ 有关，像素尺寸是指图像传感器上每个像素的物理尺寸，通常以微米 $(μ m)$ 为单位。它是指在传感器上每个像素所占据的面积。IMX249芯片的像素尺寸为 $\mu m \times 5.86 \mu m$ 。所以分辨率为 $1920(11.33/5.86\times1000) \times 1200(7.13/5.85\times1000)$ ，也就是2.3M(230万)的分辨率。
什么是内参?
内参可以完成相机坐标系中点P到像素坐标系的投影。也就是说点P的反射光线，经过光心以及透镜的折射以后，会落在像素坐标系的那个像素坐标。以下面的公式讲解:
$\begin{bmatrix} u\\ v\\ 1\\ \end{bmatrix} = {1 \over z_c} \begin{bmatrix} f_x&0&c_x\\ 0& f_y&c_y\\ 0&0&1\\ \end{bmatrix} \begin{bmatrix} x_c\\ y_c\\ z_c\\ \end{bmatrix} (1) \\ \ \\ \left\{ \begin{aligned} u = {f_x \over z_c} x_c + c_x \\ v = {f_y \over z_c} x_c + c_y \\ \end{aligned} \right. \\ \ \\ \left\{ \begin{aligned} x_c ={(u - c_x) \times \sigma_u \over f} \times z_c ={(u - c_x) \over f_x} \times z_c \\ y_c ={(v - c_y) \times \sigma_v \over f} \times z_c ={(v - c_y) \over f_y} \times z_c \\ \end{aligned} \right. （2）$
上式为点P在相机坐标系中的坐标 $x_c,y_c,z_c)$ 与像素坐标系坐标 $(u, v)$ 的关系。遵循相似三角形给原则，如下图:

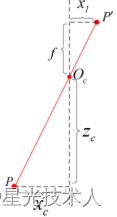
其中， f为焦距， $p$ 是相机坐标系中的坐标位置， $p^{'}$ 为图像物理坐标系中的坐标位置。 $p'(x_l,y_l)$ 在像素坐标中的位置为:
${(x_l - c_x) \times \sigma_u \over f} \\ \ \\ v = {(y_l - c_y) \times \sigma_v \over f} \\ \ \\ f_x = {f \over \sigma_u }\\ \ \\ f_y = {f \over \sigma_v}$

所以说，内参的作用就是完成尺度转化和中心化。

点P在像素坐标系中的像素代表了光心与点P连线方向的射线上的所有点，如果你把式子(1)的相机坐标系坐标的xyz同时缩放m倍，得到的uv像素点是一致的。
反过来思考，如果给你一个像素点坐标uv, 以及内参矩阵，你可以得到该点在相机坐标系下的笛卡尔三维坐标吗？答案是不行的，因为缺少了深度信息。每个像素点都是一条射线，但是射线的长度你不知道。但是如果允许你进行深度的采样呐？也就是说假如相机的可见距离是200，那么采样2000个深度(2000个 $z_c$ )，就可以得到2000个坐标点位置，这2000个点都在射线上，这也就是自动驾驶中LSS的原理。
如果某个像素是个接地点，那么也算是获得了深度的信息。根据相机距离地面的高度，就可以获得深度。注意这里的相机光轴需要水平，如果不水平，需要使用一个水平状态的相机坐标系作为中转，这就是接地点测距的原理。针孔相机中借助了深度为1的平面。

图像传感器尺寸，像素尺寸，焦距，FOV角之间的关系
假定某相机镜头焦距为f(mm)，芯片尺寸为 $w, h$ ，垂直FOV角为 $\theta_v$ ，水平FOV角度为 $\theta_u$ 。那么，
$tan({\theta_u \over 2}) = {w \over 2 \times f} \\ \ \\ \theta_u = 2 \times arctan({w \over 2 \times f}) \\ \ \\ \theta_v= 2 \times arctan({w \over 2 \times f})$
给定某个物体所占的像素大小，得到物体真实大小深度的原理
假定有棵树与相机水平，真实高度为H，v方向占用像素M个，像素尺寸 $\sigma_v$ ，焦距 $f$ ，深度为z。则：
$\over M \times \sigma_v} = {z \over f}$

图片的伸缩和裁剪变换

上文已经讲解了内参的作用，给定一系列相机系下的三维点 $P\{p_1, p_2, ... , p_n\},p_i \in R_3$ 。相机内参 $\in R_{3\times3}$ 。计算对应的像素点，将这团三维点投影到图片上。
如果图片发生了裁剪和缩放，为了使得这团激光点还可以正确的完成反投影，需要怎么调整内参？
假定原始的内外参矩阵为:
$\begin{bmatrix} f_x & 0 & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1 \\ \end{bmatrix} ,$

图片缩放，在w方向缩放 $t_w$ 倍，在h方向缩放 $t_h$ 倍
$\begin{bmatrix} u_{new}\\ v_{new}\\ 1\\ \end{bmatrix} = {1 \over z_c} \begin{bmatrix} t_wf_x&0&t_wc_x\\ 0& t_hf_y&t_hc_y\\ 0&0&1\\ \end{bmatrix} \begin{bmatrix} x_c\\ y_c\\ z_c\\ \end{bmatrix}$
图片裁剪，以原图上的像素位置 $m_x,m_y)$ 为左上角裁剪
$\begin{bmatrix} u_{new}\\ v_{new}\\ 1\\ \end{bmatrix} = {1 \over z_c} \begin{bmatrix} f_x&0&c_x - m_x \\ 0& f_y&c_y-m_y \\ 0&0&1\\ \end{bmatrix} \begin{bmatrix} x_c\\ y_c\\ z_c\\ \end{bmatrix}$
先从 $m_x,m_y)$ 开始裁剪，裁剪后的图片尺寸是原始尺寸的 $T_1$ 倍，随后把裁剪后的图片扩大到原始图片的 $T_2$ 倍
$\begin{bmatrix} u\\ v\\ 1\\ \end{bmatrix} = {1 \over z_c} \begin{bmatrix} {T_2 \over T_1 }f_x&0&{T_2 \over T_1 }(c_x - m_x)\\ 0&{T_2 \over T_1 } f_y&{T_2 \over T_1 }(c_y - m_y)\\ 0&0&1\\ \end{bmatrix} \begin{bmatrix} x_c\\ y_c\\ z_c\\ \end{bmatrix}$
先缩放后裁剪。先缩放到原始图片的 $T_1$ 倍，然后从缩放后的图片的 $m_x,m_y)$ 开始裁剪。
$\begin{bmatrix} u\\ v\\ 1\\ \end{bmatrix} = {1 \over z_c} \begin{bmatrix} T_1f_x&0&T_1c_x - m_x\\ 0& T_1f_y&T_1c_y - m_y\\ 0&0&1\\ \end{bmatrix} \begin{bmatrix} x_c\\ y_c\\ z_c\\ \end{bmatrix}$

内参标定———非线性优化

相机的内参标定通常是转化为非线性优化的问题，通过多组3D空间点和像素点的一一对应关系，构建优化函数，然后通过LM算法或者高斯牛顿计算。
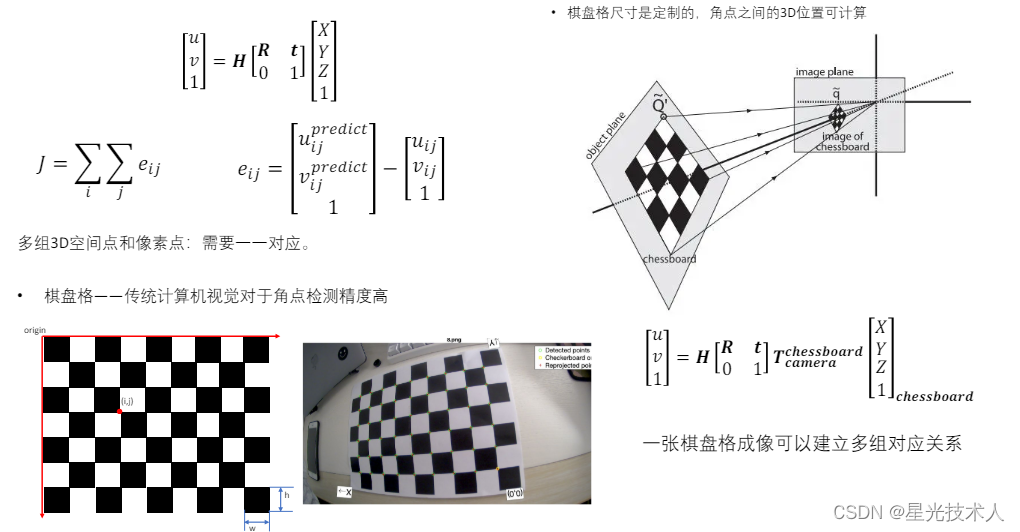
在这里插入图片描述
构建棋盘格坐标系，原点为棋盘格左上角点，X/Y轴分别为棋盘格的两条边，Z轴垂直棋盘格平面。
根据棋盘格的尺寸，可以得到一系列棋盘格的交叉点3D坐标 $P_{chessboard}\{p_0,p_1,p_2,...,p_n\},p \in R_3$ 。通过角点检测算法得到图片中的棋盘格格子角点的像素坐标(可以使用计算机视觉中的Harris算法，可以使用Opencv中的API)。最后根据外参(这里的外参是棋盘格坐标系到相机坐标系的变变换关系 $T_{chessboard}^{camera}$ ，图中是 $T_{camera}^{chessboard}$ ,我的习惯是写成前者，表示一个点从chessboar系到camera系的变换)和相机内参构建一系列的方程，通常至少需要四组点的对应关系。
那么现在的问题就是，我们得到了若干组的像素点与3D点的对应关系，怎么求解这里的内参矩阵和外参矩阵呐？这就需要提到张正友标定。

张式标定法的大致思路如下:
那么现在的问题就是，我们得到了若干组的像素点与3D点的对应关系，怎么求解这里的内参矩阵和外参矩阵呐？这就需要提到张正友标定。
张式标定法的大致思路如下:

准备一个张正标定法的棋盘格，棋盘格大小已知，用相机对其进行不同角度的拍摄，得到一组图像
对图像中的特征点如标定板的角点进行检测，得到标定板角点的像素坐标值(畸变后的)，根据已知的棋盘格大小和世界坐标系(这里将棋盘格坐标系作为世界坐标系)原点，计算得到标定板角点的物理坐标值
求解内参矩阵和外参矩阵的点乘
根据物理坐标系和像素坐标系值(就当成是没有畸变的像素点坐标)的关系，求出H矩阵(内参矩阵点乘外参矩阵)，进而构造v矩阵，求解B矩阵，最后利用B矩阵求解内参矩阵，最后求解每张图片对应的相机外参矩阵。(这里的H,D,V,B矩阵的含义下文会介绍)
这里的求解过程都是将角点像素值作为没有畸变的情况下进行的，存在误差
求解畸变参数
根据一组畸变后的角点像素值以及对应的理想像素值，构造D矩阵，计算畸变参数(这里的理想像素坐标值和畸变后的角点像素坐标的怎么得到？)
利用L-M算法对第4步目标函数进行求解，进行参数优化

张正定标定详细原理(含公式推导)

在梳理这个问题之前，需要明白的是不同位置不同角度的标定板与相机坐标系之间的外参矩阵 $T_{chessboard}^{camera}$ 是不同的，但是同一个位置标定板的不同角点坐标与相机之间的外参矩阵是一样的，还有就是所有位置所有角度拍摄的照片对应的内参是一样的。

第一步, 构建求解H矩阵
H矩阵其实就是内参矩阵与外参矩阵的乘积，但是又有点不同，因为棋盘格坐标系Z轴垂直棋盘格平面的缘故，所以这里可以完成简化，不需要旋转矩阵的第三列。
记点棋盘格坐标系P的坐标为 ${x_{chessboard},y_{chessboard},z_{chessboard}\}$ ,内参矩阵记为 $I$ ，外参矩阵记为 $T_{chessboard}^{camera}$ ,对应的像素点坐标为 ${u,v\}$ ，点P在相机坐标系下的z轴坐标为 $z_{cam}$ 。由此得到如下公式:
$\begin{align} z_{cam}\begin{bmatrix} u\\ v\\ 1\\ \end{bmatrix} &= I \cdot T_{chessboard}^{cam} \cdot \begin{bmatrix} x_{chessboard}\\ y_{chessboard}\\ z_{chessboard}\\ 1\\ \end{bmatrix} , I \in R_{3 \times 4}, T_{chessboard}^{camera} \in R_{4\times4} \\ z_{cam}\begin{bmatrix} u\\ v\\ 1\\ \end{bmatrix} &= I \cdot \begin{bmatrix} r_1, r_2, r_3, t\end{bmatrix} \cdot \begin{bmatrix} x_{chessboard}\\ y_{chessboard}\\ z_{chessboard}\\ 1\\ \end{bmatrix} , I \in R_{3 \times 4}, r_i \in R_4 \\ \end{align}$

因为棋盘坐标系垂直于棋盘格平面，所以这里的棋盘格点P的z轴坐标为0，因此得，

$\begin{align} z_{cam}\begin{bmatrix} u\\ v\\ 1\\ \end{bmatrix} &= I \cdot \begin{bmatrix} r_1, r_2, t\end{bmatrix} \cdot \begin{bmatrix} x_{chessboard}\\ y_{chessboard}\\ 1\\ \end{bmatrix} , I \in R_{3 \times 3}, r_i \in R_3 \\ \ \\ z_{cam} \bar{m} &= H \cdot \bar{M}, H \in R_{3 \times 3},\bar{m} \in R_3, \bar{M} \in R_3 \\ \ \\ H &= I \cdot \begin{bmatrix} r_1, r_2, t\end{bmatrix} = \begin{bmatrix} h_{11} &h_{12} & h_{13} \\ h_{21} &h_{22} & h_{23} \\ h_{31} &h_{32} & h_{33} \\ \end{bmatrix} \\ \ \\ I &= \begin{bmatrix} h_{11} &h_{12} & h_{13} \\ h_{21} &h_{22} & h_{23} \\ h_{31} &h_{32} & h_{33} \\ \end{bmatrix} \\ \ \\ u&=\frac{h_{11} x_{chessboard}+h_{12} x_{chessboard}+h_{13}}{h_{31} x_{chessboard}+h_{32} x_{chessboard}+h_{33}} \times {1 \over z_{cam}}\\ v&=\frac{h_{21} x_{chessboard}+h_{22} x_{chessboard}+h_{23}}{h_{31} x_{chessboard}+h_{32} x_{chessboard}+h_{33}} \times {1 \over z_{cam}} \end{align}$

每个对应关系可以构建上式(8)(9)两个式子，式(7)的9个参数中有个其次坐标，因为需要四个棋盘格系的坐标点，构成8个等式完成H矩阵的8个参数的求解。注意这四个点需要来自同一个位置的棋盘格标定板，因为H矩阵包含了外参，这8个等式的H矩阵需要保持一致。

第二步，构建 $V$ 矩阵，求解 $B$ 矩阵

B矩阵需要内参矩阵来求解， $B = I^{-T}I^{-1}$ 。为什么需要这个参数请看下边的分析

根据上文知道， $r_1,r_2$ 是外参矩阵的前两列，这两个单位列向量正交，即 $r_1^Tr_2=0$ ，由此可以得到下列的过程，记矩阵 $H=[h_1,h_2,h_3],h_i \in R_3$
$\begin{align} [h_1,h_2,h_3] &= I[r_1,r_2,t] \\ h_1 &= Ir_1, h_2 = Ir_2 \\ r_1 &= I^{-1}h_1, r_2=I^{-1}h_2\\ r_1^Tr_2 &= h_1^TI^{-T}I^{-1}h_2=0 \\ r_2^Tr_1 &= h_2^TI^{-T}I^{-1}h_1=0 \\ \ \\ I &= \begin{bmatrix} f_x & \gamma & u_x \\ 0 & f_y & u_y \\ 0 & 0 & 1 \\ \end{bmatrix} \end{align}$
记矩阵 $B$ 为:
$\begin{align} B &= I^{-T}I^{-1} = \begin{bmatrix} b_{11} & b_{12} & b_{13} \\ b_{21} & b_{22} & b_{23} \\ b_{31} & b_{32} & b_{33} \end{bmatrix} =\left[\begin{array}{ccc} \frac{1}{f_x^{2}} & -\frac{\gamma}{f_x^{2} f_y} & \frac{c_{y} \gamma-c_{x} f_y}{f_x^{2} f_y} \\ -\frac{\gamma}{f_x^{2} f_y} & \frac{\gamma}{f_x^{2} f_y}+\frac{1}{f_y^{2}} & -\frac{\gamma\left(c_{y} \gamma-c_{x} f_y\right)}{f_x^{2} f_y^{2}}-\frac{c_{y}^{2}}{f_y^{2}} \\ \frac{c_{y} \gamma-c_{x} f_y}{f_x^{2} f_y} & -\frac{\gamma\left(c_{y} \gamma-c_{x} f_y\right)}{f_x^{2} f_y^{2}}-\frac{c_{y}^{2}}{f_y^{2}} & \frac{\left(c_{y} \gamma-c_{x} f_y\right)^{2}}{f_x^{2} f_y^{2}}+\frac{c_{y}^{2}}{f_y^{2}}+1 \end{array}\right] \\ B &= \begin{bmatrix} b_{11} & b_{12} & b_{13} \\ b_{12} & b_{22} & b_{23} \\ b_{13} & b_{23} & b_{33} \end{bmatrix} \end{align}$
由式子(16)(17)我们可以知道在H矩阵已知的情况下，每个棋盘格位姿可以得到两个等式，内参据矩阵 $I$ 有5个参数需要求解，矩阵B有九个参数，但是因为矩阵B是个对称阵，所以矩阵B只剩下6个参数需要求解，因此我们需要三个棋盘格的位姿来完成6个等式的构建(每个棋盘格位姿选取超过4个角点坐标求出对应的H矩阵)。由此我们就求出了B矩阵，B矩阵与内参矩阵联系紧密。

因为B矩阵是个对称阵，因此B矩阵中还有6个参数需要求解，记作b。
$b = [b_{11},b_{12},b_{22},b_{21},b_{22},b_{33}]^T$
因此， $h_1^TI^{-T}I^{-1}h_2=0$ 可以完成下述推导，
$\begin{align} h_1^TI^{-T}I^{-1}h_2 &= h_1 B h_2= [h_{11},h_{12},h_{13}] \begin{bmatrix} b_{11} & b_{12} & b_{13} \\ b_{21} & b_{22} & b_{23} \\ b_{31} & b_{32} & b_{33} \end{bmatrix} \begin{bmatrix} h_{21} \\ h_{22} \\ h_{23} \end{bmatrix} = v_{ij}b \\ v_{12}&=\left[h_{11} h_{21}, h_{11} h_{22}+h_{12} h_{21}, h_{12} h_{22}, h_{13} h_{21}+h_{11} h_{23}, h_{13} h_{22}+h_{12} h_{23}, h_{13} h_{23}\right]^{T} \end{align}$
然后结合式子(16)(17)，可以得到下列等式，
$\begin{align} \begin{bmatrix} v_{12}^T \\ v_{11}^T - v_{22}^T \end{bmatrix} \cdot [b_{11},b_{12},b_{22},b_{21},b_{22},b_{33}]^T =\begin{bmatrix} v_{12}^T \\ v_{11}^T - v_{22}^T \end{bmatrix} b = 0 \end{align}$
因此，每个姿态的标定板(通过标定板上的四个角点位置)得到的H矩阵的帮助下，可以构建两个方程，限制B矩阵(B矩阵来源自内参，所以所有标定板姿态对应的B矩阵都一样)的两个自由度(B矩阵只有六个自由度）。所以我们需要三个位置姿态的标定板对应的H矩阵来构建6个方程，完成B矩阵6个自由度的限制。

记第一个标定板对应的V矩阵为 $v'_{12},v'_{11},v'_{22}$ ，第二个标定板对应的V矩阵为 $v''_{12},v''_{11},v''_{22}$ ，第三个标定板对应的V矩阵为 $v'''_{12},v'''_{11},v'''_{22}$ 。那么结合式(24)，我们可以得到，
$\begin{align} \begin{bmatrix} {v'}_{12}^T \\ {v'}_{11}^T - {v'}_{22}^T \\ {v''}_{12}^T \\ {v''}_{11}^T - {v''}_{22}^T \\ {v'''}_{12}^T \\ {v'''}_{11}^T - {v'''}_{22}^T \end{bmatrix} \cdot \begin{bmatrix} b_{11} \\ b_{12} \\ b_{22} \\ b_{31} \\ b_{32} \\ b_{33} \end{bmatrix} = A \cdot b = 0 \end{align}$
利用非线性优化的方式，就能求出矩阵b。

第三步，利用 $B$ 矩阵求解内参矩阵 $I$
得到B矩阵以后，通过Cholesky分解得到相机的内参数
$\begin{align} f_x & =\sqrt{\frac{1}{b_{11}}} \\ f_y & =\sqrt{\frac{b_{11}}{b_{11} b_{22}-b_{12}^{2}}} \\ \gamma & =-f_x^{2} f_y b_{12} \\ c_{y} & =\frac{b_{12} b_{13}-b_{11} b_{23}}{b_{11} b_{22}-b_{12}^{2}} \\ c_{x} & =\frac{c_{y} \gamma}{f_y}-f_x^{2} b_{13} \end{align}$
第四步，结合H矩阵和内参矩阵，求出每个姿态棋盘格的外参
第三步结束以后，得到了相机的内参矩阵。然后结合每个位姿棋盘格求出的H矩阵和上一步求出的内参矩阵求解每个位置姿态的棋盘格坐标系与相机坐标系之间的转换关系 $T_{chessboard}^{camera}$ 。
结合式(15)，具体计算步骤如下：
$\begin{align} r_1 &= I^{-1}h_1 \\ r_2 &= I^{-1}h_2 \\ r_3 &= r_1 \times r_2 \\ t &= I^{-1}h_3 \\ \end{align}$
到这里，我们已经得到了使用的所有位姿棋盘格与相机坐标系直接的外参关系 $T_{chessboard}^{camera}$ ，以及相机的内参。

总结一下之前的四步: 首先每个棋盘格姿态我们提取四个角点，构建8个方程，完成H矩阵的求解(H矩阵是内参矩阵和该棋盘格坐标系与相机坐标系的乘积，因此每个位资的棋盘格都对应一个H矩阵)；然后另外选取2个位姿的棋盘格，求出另外两个H矩阵。再然后每个H矩阵构建一个两个方程，三个H矩阵构建六个方程，最后构建一个方程组，自变量就是B矩阵的6个参数，系数矩阵记为V矩阵，使用非线性优化的方式求出B矩阵；在然后借助Cholesky分解完成内参矩阵的求解；最后求解相机坐标系与所有棋盘格姿态的外参联系 $T_{chessboard}^{camera}$ 。需要注意的是，上述的过程都是在假设没有畸变的情况下，也就是说式(3)是在无畸变的情况下构建的等式。所以求出的H矩阵，也就基于无畸变的假设，进而造成后续的B矩阵，I矩阵和外参矩阵都有一定的误差存在。所以下边的步骤将解决这里的误差

第五步，求解畸变参数
求畸变参数的过程也是最小化误差的过程，完成理想像素点坐标与畸变情况下的像素点坐标之间误差的最小化，最后构建一个方程组，使用LM算法完成最后畸变参数的求解。
记理想像素坐标为 $(u, v)$ ，对应在图像物理坐标系的坐标为 $x_l,y_l)$ ，距离芯片中心的距离 $r_c=\sqrt{x_l^2 + y_l^2}$ ；携带畸变的像素坐标为 $(u^{'}, v^{'})$ ，对应在图像物理坐标系的坐标为 $x_l^{'},y_l^{'})$ ；感光芯片的像素尺寸为 $(\sigma_u,\sigma_v)$ ；畸变参数为 $k_1,k_2,k_3,k_4$ 。为了方便写公式，下文仅对 $k_1，k_2$ 进行求解， $k_3,k_4$ 同理拓展即可。
$\begin{align} u &= {x_l \over \sigma_u} + c_x， u' = {x_l^{'} \over \sigma_u} + c_x\\ v &= {y_l \over \sigma_v} + c_y，v' = {y_l^{'} \over \sigma_v} + c_y \\ \end{align}$
结合式(35)和(36)可以推出，
$\begin{align} u - c_x &= (u' - c_x) \times (1 + k_1r_c^2 + k_2r_c^4) \\ v- c_y &= (v' - c_y) \times (1 + k_1r_c^2 + k_2r_c^4) \\ \end{align}$
进一步，得
$\begin{align} \begin{bmatrix} (c_x - u')r_c^2 & (c_x - u')r_c^4 \\ (c_y - v')r_c^2 & (c_y - v')r_c^4 \\ \end{bmatrix} \begin{bmatrix} k_1 \\ k_2 \end{bmatrix} = \begin{bmatrix} u' - u \\ v' - v \end{bmatrix} \end{align}$
上式中的理想像素坐标点，通过前四步求出的理想内外参矩阵完成棋盘格坐标系3D点的重投影，得到理想的像素点坐标。携带畸变的像素点坐标通过直接对图片进行角点检测得到对应的像素点。每个3D角点和像素点都可以构建式(39)的两个方程。为了可以最小化误差的影响，我们选择已经求出H矩阵的多个棋盘格(m个)位姿的多个3D角点和对应的图片角点像素坐标(n个)，构建mn个方程，参照式子(39)的形式整理为矩阵相乘的形式。
$\begin{align} \begin{bmatrix} (c_x - u')r_c^2 & (c_x - u')r_c^4 \\ (c_y - v')r_c^2 & (c_y - v')r_c^4 \\ . & . \\ . & . \\ . & . \\ . & . \\ \end{bmatrix} \begin{bmatrix} k_1 \\ k_2 \end{bmatrix} = \begin{bmatrix} u' - u \\ v' - v \\ ... \\ ... \\ ... \\ ...\\ \end{bmatrix} \end{align}$
记作，
$\begin{align} D \cdot k &= d \\ D &= \begin{bmatrix} (c_x - u')r_c^2 & (c_x - u')r_c^4 \\ (c_y - v')r_c^2 & (c_y - v')r_c^4 \\ . & . \\ . & . \\ . & . \\ . & . \\ \end{bmatrix} \\ d&= \begin{bmatrix} u' - u \\ v' - v \\ ... \\ ... \\ ... \\ ...\\ \end{bmatrix} \end{align}$
使用最小二乘法，得到最后的结果
$(D^T \cdot D)^{-1} \cdot D^T \cdot d$
至此，就已经算出了所有的参数。
第六步，重投影，根据重投影误差优化参数
详情看代码