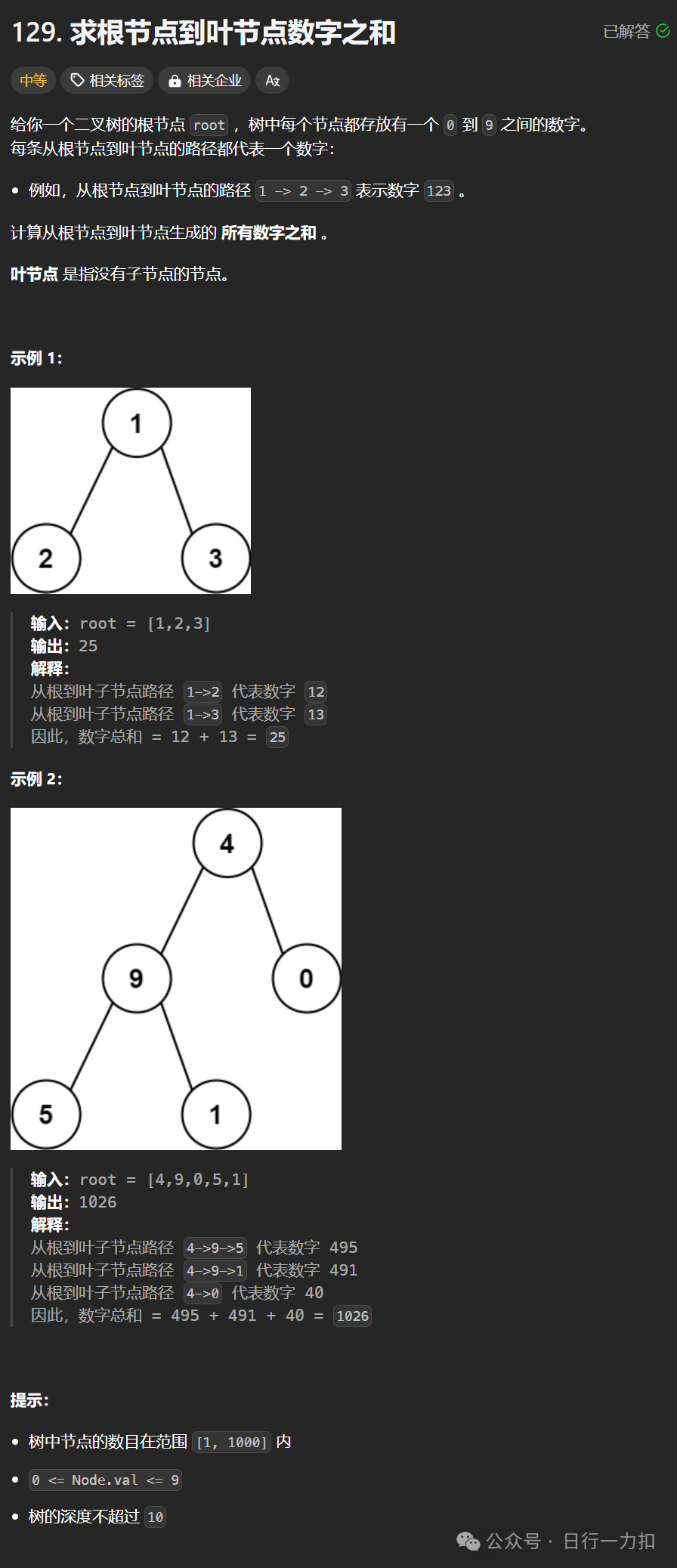
1. 题目描述
2. 题目分析与解析
2.1 思路一——DFS
-
理解问题: 首先要理解题目的要求,即对于给定的二叉树,我们需要找出从根节点到所有叶子节点的所有路径,然后将每一条路径上的数字组成一个整数,最后求出这些整数的和。
-
定义递归函数: 递归函数的目的是遍历树,同时记录下遍历到当前节点为止形成的数字。递归函数可以接收两个参数:当前节点和当前路径代表的数字。
-
编写递归逻辑:
-
递归出口:如果当前节点是叶子节点(即没有左右子节点),则将当前路径代表的数字加到总和中。
-
递归过程:如果当前节点不是叶子节点,则对其左右子节点进行递归调用,同时更新路径代表的数字。
-
-
计算路径数字: 在从根节点向下遍历的过程中,每向下一层,路径代表的数字就要左移一位(即乘以10),然后加上当前节点的值。
-
全局变量或返回值: 为了存储总和,可以使用全局变量,或者在递归函数中返回当前累加的和,并在上一层递归中将返回值累加。
-
开始递归: 最初调用递归函数时,从根节点开始,并且当前路径数字为0。
-
边界条件: 考虑空树或只有一个节点的树的边界条件。
2.2 思路二——BFS
-
理解BFS和递归的区别: 广度优先搜索(BFS)与递归方法不同,它使用队列来迭代地遍历树的每一层。在BFS中,我们按照树的层级从上到下逐层遍历节点,而递归方法通常是深度优先搜索(DFS),从根节点开始直到叶子节点,然后回溯。
-
初始化: 在方法中,首先检查根节点是否为null。如果是,返回0。否则,初始化一个队列
layer来保存树的每层节点。 -
处理根节点: 将根节点加入队列。
-
层序遍历: 当队列不为空时,循环执行以下步骤:
-
从队列中取出一个节点作为当前节点。
-
检查当前节点是否有左子节点,如果有,则计算左子节点代表的新数字并更新左子节点的值,然后将左子节点加入队列。
-
检查当前节点是否有右子节点,如果有,同样计算右子节点代表的新数字并更新右子节点的值,然后将右子节点加入队列。
-
如果当前节点是叶子节点(没有左右子节点),将它的值加到结果
result中。
-
-
更新节点值: 在每个非叶子节点上,更新其左右子节点的值为
当前节点的值*10+子节点的原始值。这一步模拟深度优先过程中的路径数字累加。 -
累加叶子节点的值: 对于每个叶子节点,其值现在代表了从根节点到该叶子节点的路径数字。将这些数字累加到结果变量
result中。 -
返回结果: 遍历完成后,返回
result,它包含了所有从根节点到叶子节点路径所代表的数字之和。
3. 代码实现
3.1 思路一
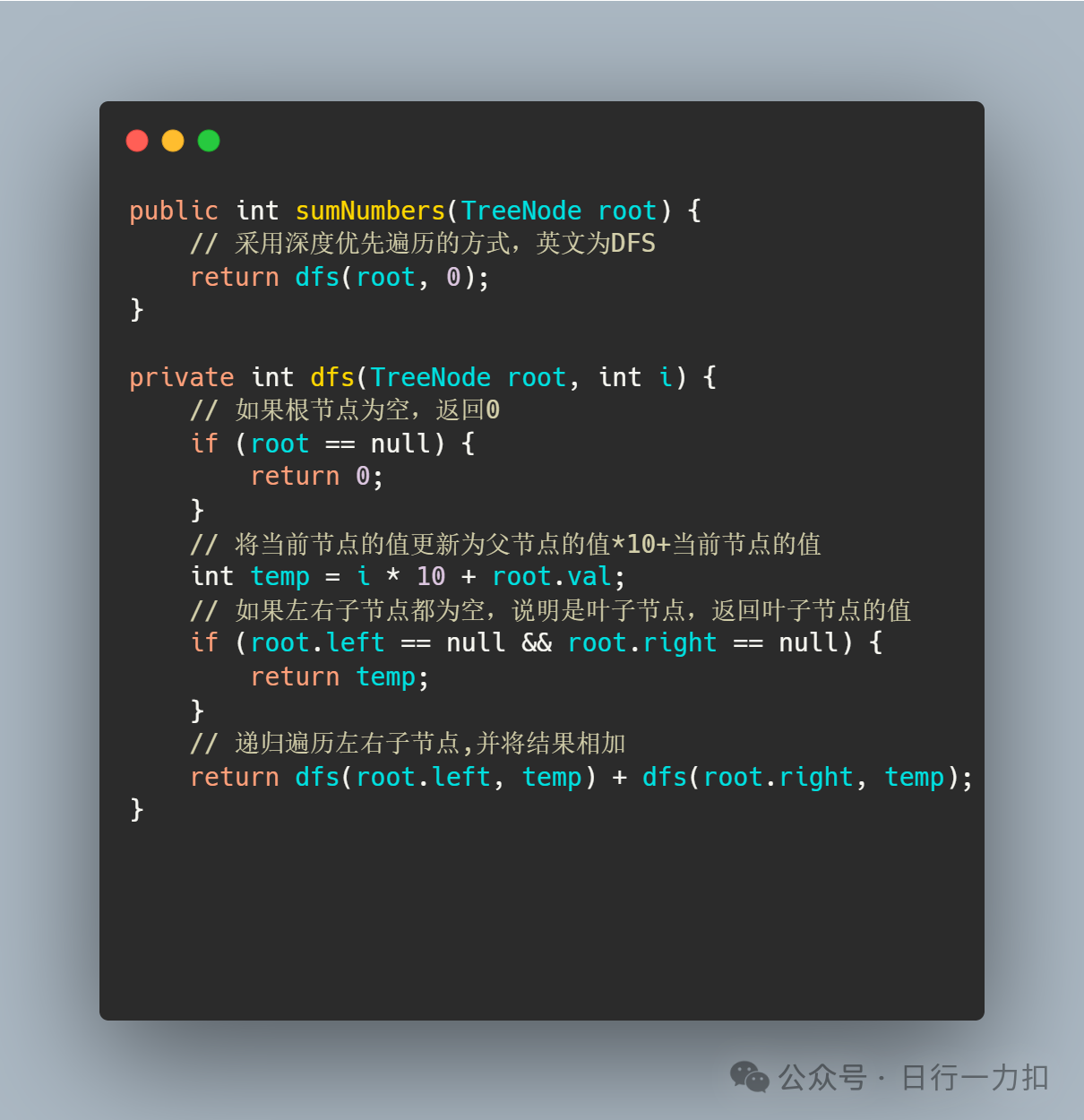
3.2 思路二
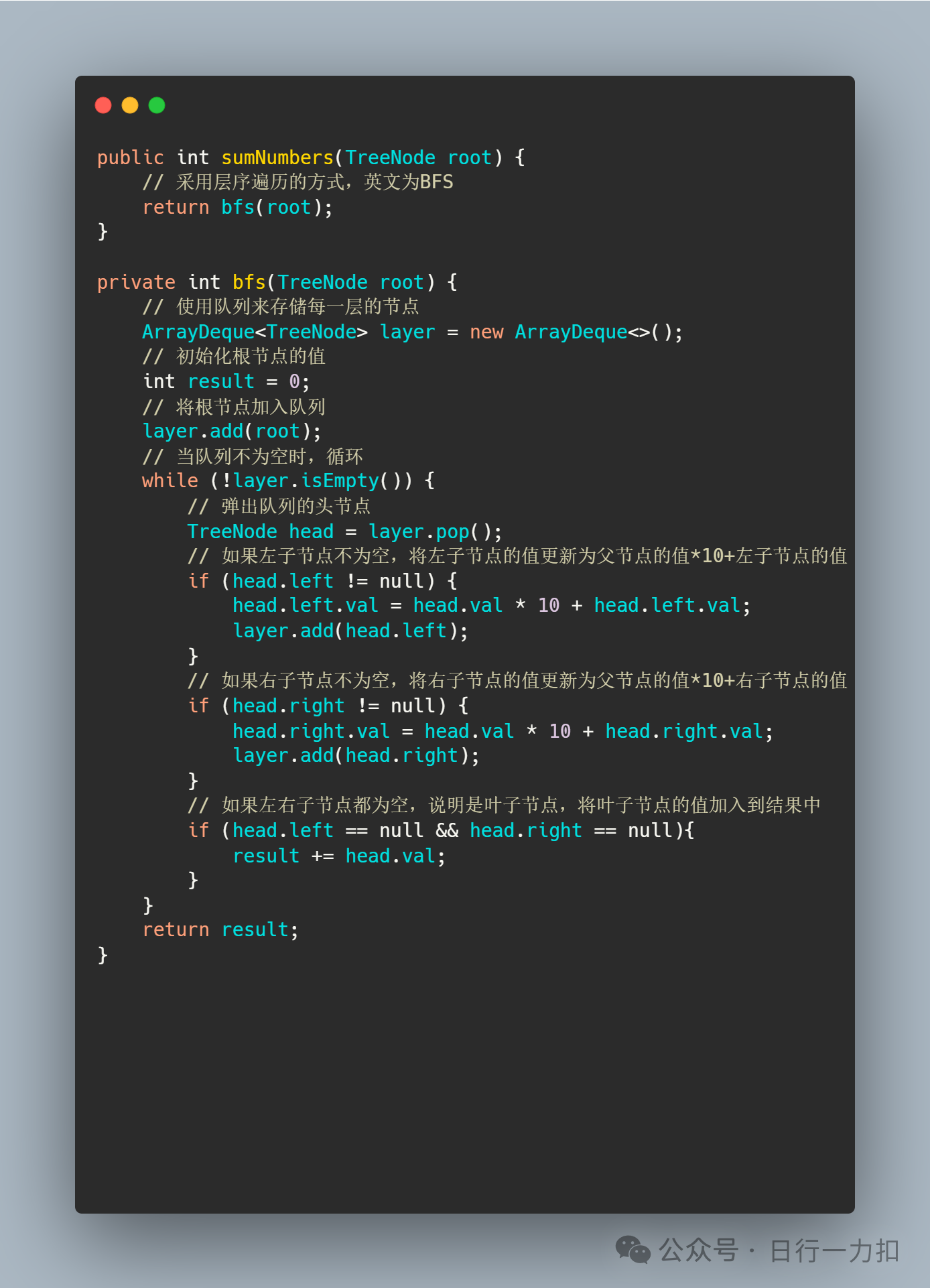
4. 相关复杂度分析
BFS方法(层序遍历)
-
时间复杂度:O(N),其中N是树中节点的数量。在BFS中,每个节点恰好被访问一次,无论是内部节点还是叶子节点。
-
空间复杂度:最坏情况下(完全二叉树)是O(N),因为队列需要存储一层中的所有节点,对于完全二叉树来说,最底层的节点大约占总节点数的一半。在最好的情况下(高度倾斜的树),空间复杂度是O(1),因为队列中同时只有一个元素。
DFS方法(深度优先遍历)
-
时间复杂度:O(N),与BFS相同,每个节点恰好被访问一次。
-
空间复杂度:最坏情况下(完全非平衡树,即链表形状)是O(N),因为要存储递归栈。在最好情况下(完全二叉树),空间复杂度是O(logN),对应于树的高度。
总结
-
对于时间复杂度,两种方法都是O(N),因为两种方法都会访问树中的每一个节点。
-
对于空间复杂度,BFS和DFS之间的差异通常依赖于树的形状。对于大多数情况,DFS的空间复杂度较低,因为它的最坏情况是高度倾斜的树。而BFS在最坏情况下可能需要存储许多节点。
需要注意的是,DFS递归的空间复杂度也包括隐式的调用栈。在实际情况中,如果树非常深,DFS可能会因为堆栈溢出而不如BFS稳定。相反,如果树非常宽,则BFS可能会因为队列变得非常大而消耗更多内存。
当然需要提示一下:我的代码中BFS方法修改了树的结构,因为它实际上改变了节点的值来存储路径总和。这在实际应用中可能是不可取的,因为它破坏了原始数据,如果像解决这个问题就是采用一个和队列相同结构的部分存储值就行。DFS方法则没有这个问题,它保持了树的结构不变。