---

前言

一个本硕双非的小菜鸡，备战24年秋招，计划刷完hot100和剑指Offer的刷题计划，加油！
根据要求，每一道题都要写出两种以上的解题技巧。

一、300. 最长递增子序列（HOT100）

300. 最长递增子序列
Note：贪心+二分
通过维护一个数组，表示长度为 i 的最长上升子序列的末尾元素的最小值，用 len 记录目前最长上升子序列的长度。
循环遍历数组中的元素，如果当前元素 nums[i] 大于 vec[len]，说明可以将 nums[i] 添加到当前的最长递增子序列的末尾，因此将 len 加 1，并将 nums[i] 赋值给vec[len]。
如果当前元素 nums[i] 小于 vec[len]，说明 nums[i] 不能添加到当前的最长递增子序列的末尾。此时需要在 vec 中找到一个合适的位置来插入 nums[i]，使得插入后的 vec 仍然是一个递增序列。通过二分查找找到第一个大于或等于 nums[i] 的元素的位置 pos，然后将 nums[i] 插入到 vec[pos + 1] 的位置。

class Solution {
public:int lengthOfLIS(vector<int>& nums) {int len = 1;int size = nums.size();if (size == 0) return 0;vector<int> vec(size + 1, 0);vec[len] = nums[0];for (int i = 1; i < size; i++) {if (nums[i] > vec[len]) {vec[++len] = nums[i];} else {int left = 1, right = len, pos = 0;while (left <= right) {int mid = left + (right - left) / 2;if (vec[mid] < nums[i]) {pos = mid;left = mid + 1;} else {right = mid - 1;}}vec[pos + 1] = nums[i];}}return len;}
};

Note：动态规划解题

class Solution {
public:int lengthOfLIS(vector<int>& nums) {if (nums.size() <= 1) return nums.size();//1. 确定dp数组（dp table）以及下标的含义//dp[i]表示i之前包括i的以nums[i]结尾的最长递增子序列的长度vector<int> dp(nums.size(), 1);int res = 0;//2. 确定递推公式//dp[i] = max(dp[i], dp[j] + 1)//3. 确定dp数组初始化//4. 确定遍历顺序for (int i = 1; i < nums.size(); i++) {for (int j = 0; j < i; j++) {if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);}res = dp[i] > res ? dp[i] : res;}//5. 确定推导dp数组return res;}
};

二、62. 不同路径（HOT100）

不同路径

Note：动态规划

class Solution {
public:int uniquePaths(int m, int n) {//1. 确定dp数组（dp table）以及下标的含义//机器人到达每个空格的路径数vector<vector<int>> dp(m, vector<int>(n, 0));//2. 确定递推公式//dp[i][j] = dp[i][j - 1] + dp[i - 1][j]//3. 确定dp数组初始化//dp[i][0] = 0, dp[0][j] = 0for (int i = 0; i < m; i++) dp[i][0] = 1;for (int i = 0; i < n; i++) dp[0][i] = 1; //4. 确定遍历顺序for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++)dp[i][j] = dp[i][j - 1] + dp[i - 1][j];}//5. 确定推导dp数组return dp[m - 1][n -1];}
};

Note：数论方法，变为一个组合问题。
公式：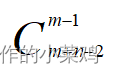

class Solution {
public:int uniquePaths(int m, int n) {long long numerator = 1; // 分子int denominator = m - 1; // 分母int count = m - 1;int t = m + n - 2;while (count--) {numerator *= (t--);while (denominator != 0 && numerator % denominator == 0) {numerator /= denominator;denominator--;}}return numerator;}
};
# 总结
祝大家都能学有所成，找到一份好工作！