1001 Typhoon
计算几何
对于每一个避难点,计算其到所有线段的距离,取min即可
AC代码:
#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
#include<deque>
#include<cmath>
#include<cstdio>
#include<iomanip>
#define endl '\n'
#define eps 1e-9
//#define int long long
using namespace std;
typedef long long ll;
const int N=1e4+10,inf=2e9;
double dist[N];
//向量表示(定义一个结构体,用坐标表示向量)
struct Point {double x,y;double len() const { //模return sqrt(x*x+y*y);}
};
Point operator+(Point a,Point b) { //加法return {a.x+b.x,a.y+b.y};
}
Point operator-(Point a,Point b) { //减法return {a.x-b.x,a.y-b.y};
}
double operator&(Point a,Point b) { //点积return a.x*b.x+a.y*b.y;
}
double operator*(Point a,Point b) { //叉积return a.x*b.y-a.y*b.x;
}
//向量的点积
double dot(Point a,Point b,Point c) {return (b-a)&(c-a);//a,b,c均为点,向量b-a与向量c-a进行点积
}
//向量的叉积
double cross(Point a,Point b,Point c) {return (b-a)*(c-a);
}
int n,m;
void solve() {cin>>m>>n;vector<Point>p(m);for(int i=0; i<m; i++) cin>>p[i].x>>p[i].y;vector<Point>s(n);for(int i=0; i<n; i++) cin>>s[i].x>>s[i].y;vector<double>dis(n,inf);//定义了一个名为dis的变量,它是一个长度为n的vector容器,其中每个元素的初始值都被设置为inffor(int i=1; i<m; i++) {//枚举线段(用向量表示)Point a=p[i-1],b=p[i];//枚举避难所for(int j=0; j<n; j++) {Point c=s[j];double d1=dot(a,b,c);//求向量b-a与向量c-a的点积double d2=dot(b,a,c);//求向量c-b与向量c-a的点积double res;if(d1<0||d2<0) {res=min((c-a).len(),(c-b).len());//点积小于0说明角度是钝角,那么垂足就在线段外,取两点最小值} else {res=cross(a,b,c)/(b-a).len();//求点到线段的垂直距离,为向量b-a与向量c-a叉积再除以向量b-a的模(面积/底)}res=fabs(res);if(res<eps) res=0;//如果答案小于精度,则直接相当于等于0dis[j]=min(dis[j],res);}}cout<<setiosflags(ios::fixed)<<setprecision(4);//保留四位小数,四舍五入,头文件为#include<iomanip>for(int i=0; i<n; i++) cout<<dis[i]<<endl;
}
int main() {ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int t=1;
// cin>>t;while(t--)solve();return 0;
}1006 Touhou Red Red Blue
法一(dp):
AC代码:
#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
#include<cstdio>
#define endl '\n'
#define get(a,b) (a*4+b)
//#define int long long
using namespace std;
typedef long long ll;
const int N=1e5+10,M=16;
int f[N][M];//f[i][j]表示当前球为i,两个袋子的球的状态为j的最大得分,袋子1中的球有4种状态,袋子2中的球也有4种状态,一共4*4=16种状态(0代表没有球,1~3代表球的颜色为R,G,B)
void solve() {string s;cin>>s;int n=s.size();for(int i=1; i<=n; i++) {int c;//表示当前球的颜色,1代表R,2代表G,3代表Bif(s[i-1]=='R') c=1;else if(s[i-1]=='G') c=2;else c=3;for(int j=0; j<M; j++) f[i][j]=f[i-1][j]; //可以选择存储或放弃UFO,我们选择扔掉它//枚举1号袋子的状态和2号袋子的状态,0代表没有球,1~3代表分别代表球的颜色为R,G,Bfor(int a=0; a<=3; a++) {for(int b=0; b<=3; b++) {//如果两个袋子都不为空if(a&&b) {//如果3个球的颜色均相同,那么三个球都消掉,得1分,和消消乐一样if(a==b&&b==c) {//得到一个附加的球放在袋子1里,此时袋子2为空for(int d=1; d<=3; d++) f[i][4*d]=max(f[i][4*d],f[i-1][get(a,b)]+1);}//如果三个球的颜色均不相同,那么3个球都会消失然后会得到两个附加的球,放到袋子1和袋子2中else if(a&&b&&a!=b&&a!=c&&b!=c) {//枚举袋子1的球的颜色for(int d=1; d<=3; d++) {//枚举袋子2的球的颜色for(int e=1; e<=3; e++) {f[i][get(d,e)]=max(f[i][get(d,e)],f[i-1][get(a,b)]);}}}//否则,扔掉袋子1中的球,将袋子2中的球移到袋子1中,并将当前球放到袋子2中else f[i][get(b,c)]=max(f[i][get(b,c)],f[i-1][get(a,b)]);}//if(a&&b)不满足,说明其中一个袋子是空的,//如果a不空,b空,那么就把c放到第二个袋子里else if(a) f[i][get(a, c)] = max(f[i][get(a, c)], f[i - 1][get(a, b)]);//如果a,b袋子均为空,那么就把c放到第一个袋子里else f[i][get(c, 0)] = max(f[i][get(c, 0)], f[i - 1][get(a, b)]);}}}int res=0;for(int i=0; i<M; i++) res=max(res,f[n][i]);cout<<res<<endl;
}
int main() {ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);memset(f[0],-0x3f,sizeof f[0]);//初始化为负无穷,因为后面要取maxf[0][0]=0;//初始状态得分为0,由此开始递推int t=1;cin>>t;while(t--)solve();return 0;
}法二(贪心):
AC代码:
#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
#include<cstdio>
#define endl '\n'
//#define int long long
using namespace std;
typedef long long ll;
void solve() {string s;cin>>s;int n=s.size();int r=0,g=0,b=0;int res=0;int t=0;//表示这一轮可以自己选几个球,初始为0for(int i=0;i<n;){//这轮可以自选一个球放在袋子1中,然后看后面两个球颜色是否相同if(t==1){if(i==n-1) break;//自选的1个球加上最后一个球一共也才2个球,不足三个球是不能消消乐的,不可以得分了,直接跳出if(s[i]==s[i+1]) t=1,res++;//,如果后两个球颜色相同,那么将这个自选的球颜色变得和后两个球颜色一样,使得三个消消乐消掉,+1分,下一轮进入t=1的状态,即下一轮可以自选一个球放到袋子1中else t=2;//如果后两个球颜色不相同,那么就使得三个球颜色均不相同,下一轮进入t=2的状态,即下一轮可以自选2个球分别放到袋子1和袋子2中i+=2;//跳过本次和下一次,因为连续三个球都消失了}//这轮可以自选两个球放在袋子1和袋子2中,我们完全可以使得这两个球和当前球颜色相同,然后消消乐消掉这三个球,+1分,下一轮else if(t==2){t=1;//凑成3个颜色相同的球,消消乐,下一轮进入t=1的状态res++;i++;//跳过本此}//只有初始状态为t=0,然后接下来就是在t=1和t=2两状态之间转来转去else{if(s[i]=='R') r++;else if(s[i]=='G') g++;else b++;if(r&&g&&b) t=2;//如果三种颜色的球的数量都不为0,那么说明三个球颜色均不相同,那么进入t=2的状态,下一轮可以自选两个球else if(r==3||b==3||g==3) t=1,res++;//如果三个球颜色均相同,那么消消乐,+1分,进入t=1的状态,下一轮可以自选一个球i++;//继续下一轮}}cout<<res<<endl;
}
int main() {ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int t=1;cin>>t;while(t--)solve();return 0;
}1007 Expectation(Easy Version)
算期望
根据样例:
一共有n局比赛
通项=组合数(n局中赢哪x局)*n局赢x局的概率*(1^m+2^m+...x^m)
然后遍历1到n,将其全部加起来
也就是:
假设赢一局的概率为p
C(n,1)*p^1*(1-p)^(n-1)*1^m+C(n,2)*p^2*(1-p)^(n-2)*(1^m+2^m)+...C(n,n)*p^n*(1^m+2^m+...+n^m)
由此,我们可以将其分为三个部分A,B以及C
然后呢,每一部分我们都可以不断地累加或者累乘

我们可以发现组合数每次都可以在上一项C(n,i)的基础上乘(n-i)/(i+1)
对于概率这一部分也是同样如此:

再次转换:
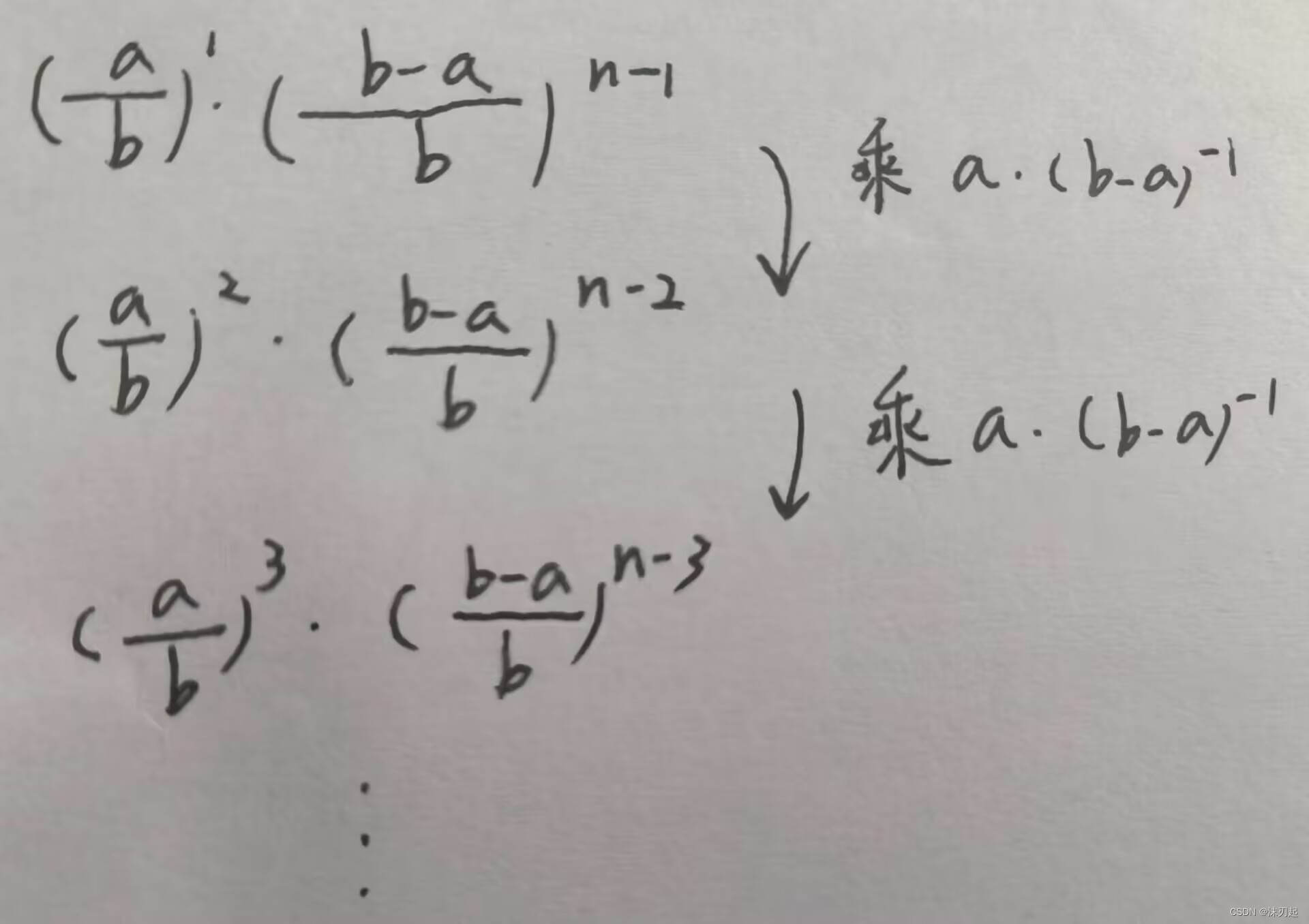
发现每次都是乘a*(b-a)^(-1)
分母始终都是b^n,所以先不用管分母,只需要当全部算完之后,最后除以一个b^n就行了
最后一部分相比之下就很简单,直接加(i+1)^m
AC代码:
#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
#include<deque>
#include<cmath>
#include<cstdio>
#define endl '\n'
#define int long long
using namespace std;
typedef long long ll;
const int mod=998244353;
int n,m,a,b;
inline int qmi(int a,int k){int res=1;while(k){if(k&1) res=(ll)res*a%mod;a=(ll)a*a%mod;k>>=1;}return res;
}
inline int inv(int x){return qmi(x,mod-2);
}
int solve() {cin>>n>>m>>a>>b;int res=0;int k=a*inv(b-a)%mod;int A=n%mod,B=qmi(b-a,n-1)*a%mod,C=1;for(int i=1;i<=n;i++){(res+=A*B%mod*C%mod)%=mod;A=A*(n-i)%mod*inv(i+1)%mod;(B*=k)%=mod;(C+=qmi(i+1,m))%=mod;}return (res*inv(qmi(b,n)))%mod;
}
signed main() {ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int t=1;cin>>t;while(t--)cout<<solve()<<endl;return 0;
}1012 Counting Stars

如图,比如说想要求以1为顶点的2-star图的数量,发现顶点1有三条边,那么就是在三条边中选择两条边的方案数,这样就用到了组合数学
原本我想的是分别求每一个cnt[i],对于每一个cnt[i],枚举所有的顶点,将每个顶点所形成的i-star图的个数加起来,但是会发现这样双重循环就超时了
for (int i = 2; i <= n - 1; i++) {for (int j = 1; j <= n; j++) {(cnt[i] += c[e[j].size()][i]) %= mod;}}可以换一种思路:枚举所有的顶点,然后我们知道该顶点的度数,就是每枚举一个顶点,就记录以该顶点可以形成的2-star,3-star...的数量,这样做的好处是不会超时,因为根据握手定理
握手定理:
![]()
所以度数之和为2*m,为2e6,也就是说时间复杂度不会超过2e6
for(int i=1;i<=n;i++){for(int j=2;j<=d[i];j++){(ans[j]+=C(deg[i],j))%=mod;}}可以这样理解,加一个cnt++,然后cnt加的次数不会超过2e6
for(int i=1;i<=n;i++){for(int j=2;j<=d[i];j++){(ans[j]+=C(deg[i],j))%=mod,cnt++;}}现在主要就是求组合数的问题,因为n太大了,所以求组合数不好求
我们发现C(n,1)=n/1,C(n,2)=n*(n-1)/(1*2),C(n,3)=n*(n-1)/(1*2*3)
所以我们可以先预处理阶乘以及阶乘的逆元
AC代码:
#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
#include<deque>
#include<cmath>
#include<cstdio>
#define endl '\n'
//#define int long long
using namespace std;
typedef long long ll;
const int N=1e6+10,mod=1e9+7;
int d[N];
int fac[N],ifac[N];
int ans[N];
int n,m;
//快速幂
int qmi(int a,int k){int res=1;while(k){if(k&1) res=(ll)res*a%mod;a=(ll)a*a%mod;k>>=1;}return res;
}
//求组合数
int C(int n,int m){if(n<m) return 0;return 1ll*fac[n]*ifac[m]%mod*ifac[n-m]%mod;
}
void solve() {cin>>n>>m;for(int i=1;i<=n;i++) d[i]=ans[i]=0;for(int i=0;i<m;i++){int u,v;cin>>u>>v;d[u]++,d[v]++;}for(int i=1;i<=n;i++){for(int j=2;j<=d[i];j++){(ans[j]+=C(d[i],j))%=mod;}}int res=0;for(int i=2;i<=n-1;i++) res^=ans[i];cout<<res<<endl;
}
signed main() {ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);//预处理阶乘以及阶乘的逆元fac[0]=ifac[0]=1;//0的阶乘是1,0的阶乘的逆元也是1for(int i=1;i<N;i++) fac[i]=1ll*fac[i-1]*i%mod;//预处理阶乘ifac[N-1]=qmi(fac[N-1],mod-2);//先求出fac[N-1]的逆元,由于(n+1)!=n!*(n+1)==>n!^(-1)=(n+1)!^(-1)*(n+1),所以也可以通过递推得到阶乘的逆元for(int i=N-2;i>=1;i--) ifac[i]=1ll*ifac[i+1]*(i+1)%mod;int t=1;cin>>t;while(t--)solve();return 0;
}