前言

镜像说的好听，无非就是换下节点。

---

题目

操作给定的二叉树，将其变换为源二叉树的镜像。
数据范围：二叉树的节点数 $0\le n\le 1000$， 二叉树每个节点的值 $0\le val\le 1000$
要求： 空间复杂度 $O(n)$ 。本题也有原地操作，即空间复杂度 $O(1)$的解法，时间复杂度 $O(n)$

源二叉树

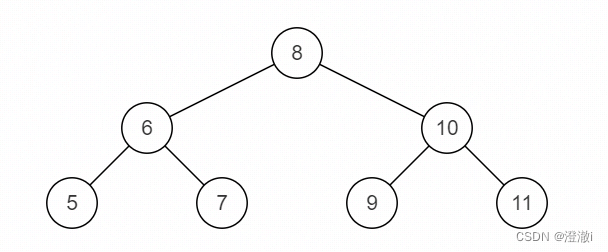
镜像二叉树

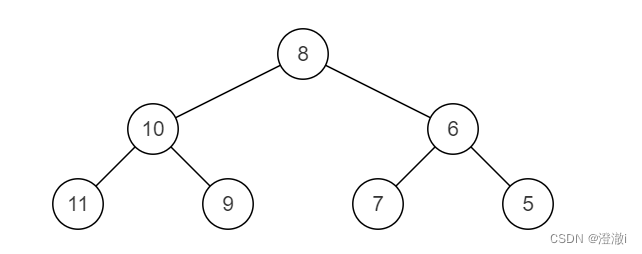
输入：{8,6,10,5,7,9,11}
返回值：{8,10,6,11,9,7,5}

示例2
输入：{}
返回值：{}

解决方案一

1.1 思路阐述

这个镜像其实就是交换下左右子树的节点罢了。

树的问题还是一样：拆分。

将一棵树进行镜像实际上就是对除了根节点外的所有节点与同属于同一个父节点的兄弟节点交换。

这里我们考虑根节点的为空的特殊情况进行单独返回。
后面就是把根节点下面的两个子节点进行交换，这里交换使用了一个temp的变量。

交换，这里是交换子树，不仅仅是交换值这么简单。所以第一次交换完之后，其实是左右子树都交换了。

接着对左右子树做同样的操作，直到轮到叶子结点。

通俗来讲，就是一个递归调用。大树分左树和右树。

时间复杂度分析：
对于每个节点，函数执行一些固定的操作，例如交换左右子树的指针，并对左右子树进行递归调用。因此，对于具有 n 个节点的二叉树，每个节点的操作时间是常数时间，因此时间复杂度为 O(n)。

空间复杂度分析：
递归调用会在函数调用栈上占用空间。在最坏的情况下，递归深度等于树的高度，因此空间复杂度取决于树的高度。对于平衡二叉树，空间复杂度为 O(log n)，其中 n 是节点数。对于不平衡的二叉树，空间复杂度可以达到 O(n)，因为递归调用可能会一直延伸到树的最深处。

综上所述，时间复杂度为 $O(n)$，空间复杂度在最坏的情况下为 $O(n)$，在最好的情况下为 $O(logn)$。

1.2 源码

/*** struct TreeNode {*	int val;*	struct TreeNode *left;*	struct TreeNode *right;*	TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* };*/
class Solution {
public:/*** 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可** * @param pRoot TreeNode类 * @return TreeNode类*/TreeNode* Mirror(TreeNode* pRoot) {if (!pRoot)return nullptr;if(pRoot->left||pRoot->right){TreeNode *temp=pRoot->left;pRoot->left=pRoot->right;pRoot->right=temp;}pRoot->left=Mirror(pRoot->left);pRoot->right=Mirror(pRoot->right);return pRoot;}
};

总结

看了下官方的题解，还有个是栈的，感觉差不多，这里就没贴了。思路都是一样的。