机器学习 | 时间序列预测中的AR模型及应用

自回归模型，通常缩写为AR模型，是时间序列分析和预测中的一个基本概念。它们在金融、经济、气候科学等各个领域都有广泛的应用。在本文中，我们将探索自回归模型，它们如何工作，它们的类型和实际例子。

自回归模型

自回归模型属于时间序列模型家族。这些模型捕捉一个观测值和几个滞后观测值（先前的时间步长）之间的关系。其核心思想是，时间序列的当前值可以表示为过去值的线性组合，带有一些随机噪声。

在数学上，p阶自回归模型，表示为AR（p），可以表示为：

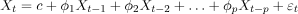
在这里插入图片描述
其中：

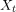
是时间t的值。
c是常数。
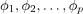
是模型参数。
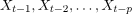
是滞后值。
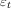
表示时间t处的白色噪声（随机误差）。

自回归模型中的自相关（ACF）

自相关，通常表示为“ACF”（自相关函数），是时间序列分析和自回归模型中的基本概念。它指的是时间序列与其滞后版本之间的相关性。在自回归模型的背景下，自相关度量时间序列的当前值与其过去值（特别是不同时滞的值）的相关程度。

以下是自回归模型中自相关概念的分解：

自相关涉及计算时间序列与其滞后版本之间的相关性。“滞后”表示序列移位的时间单位数。例如，滞后1对应于将序列与其上一个时间步进行比较，而滞后2则对应于将序列与其上一个时间步进行比较，依此类推。滞后值可帮助您计算自相关性，该自相关性用于度量时间序列中的每个观测与上一个观测的相关程度。
在一个特定的滞后的自相关性提供了洞察的时间依赖性的数据。如果自相关在某个滞后处很高，则表明当前值与该滞后处的值之间存在很强的关系。相反，如果自相关性很低或接近于零，则表明关系很弱或没有关系。
为了可视化自相关性，一种常见的方法是创建ACF图。此图显示不同滞后时的自相关系数。横轴表示滞后，纵轴表示自相关值。ACF图中的显著峰值或模式可以揭示数据的潜在时间结构。自相关在自回归模型中起着关键作用。
在p阶自回归模型中，时间序列的当前值表示为过去p值的线性组合，系数通过最小二乘或最大似然估计等方法确定。AR模型中滞后阶数（p）的选择通常依赖于ACF图的分析。
自相关也可用于评估时间序列是否平稳。在一个平稳的时间序列中，自相关应该随着滞后的增加而逐渐减小。偏离此行为可能表明非平稳性。

自回归模型的类型

AR（1）模型：

在AR（1）模型中，当前值仅取决于前一个值。
它表示为：

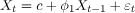
AR（p）模型：

一般p阶自回归模型包含p个滞后值。
如前文所示。

AR模型在气温预测中的应用

第1步：导入数据

在第一步中，我们导入所需的库和温度数据集。

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt# Set a random seed for reproducibility
np.random.seed(0)# Load your temperature dataset with columns "Date" and "Temperature"
data = pd.read_excel('Data.xlsx')# Make sure your "Date" column is in datetime format
data['Date'] = pd.to_datetime(data['Date'])# Sorting the data by date (if not sorted)
data = data.sort_values(by='Date')# Resetting the index
data.set_index('Date', inplace=True)data.dropna(inplace=True)

可视化数据

# Visualize the data
plt.figure(figsize=(12, 6))
plt.plot( data['Temperature '], label='Data')
plt.xlabel('Date')
plt.ylabel('Temperature')
plt.legend()
plt.title('Temperature Data')
plt.show()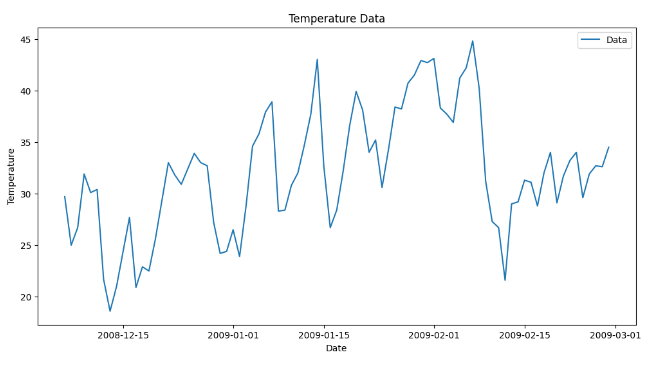

在这里插入图片描述
第2步：数据预处理

现在我们有了合成数据，我们需要对其进行预处理。我们将创建滞后特征，将数据分为训练集和测试集，并将其格式化以进行建模。

在第一步中，将滞后要素添加到数据框中。
然后完全删除具有空值的行。
然后将数据分为训练和测试数据集。
定义输入特征和目标变量。

# Adding lag features to the DataFrame
for i in range(1, 6): # Creating lag features up to 5 daysdata[f'Lag_{i}'] = data['Temperature '].shift(i)# Drop rows with NaN values resulting from creating lag features
data.dropna(inplace=True)# Split the data into training and testing sets
train_size = int(0.8 * len(data))
train_data = data[:train_size]
test_data = data[train_size:]# Define the input features (lag features) and target variabley_train = train_data['Temperature ']y_test = test_data['Temperature ']

ACF图

自相关函数（ACF）图是一种图形工具，用于可视化和评估不同滞后时间的时间序列数据的自相关性。ACF图帮助您了解时间序列的当前值如何与其过去值相关。您可以使用Stats模型库中的plot_acf函数在Python中创建ACF图。

from statsmodels.graphics.tsaplots import plot_acf
series = data['Temperature ']
plot_acf(series)
plt.show()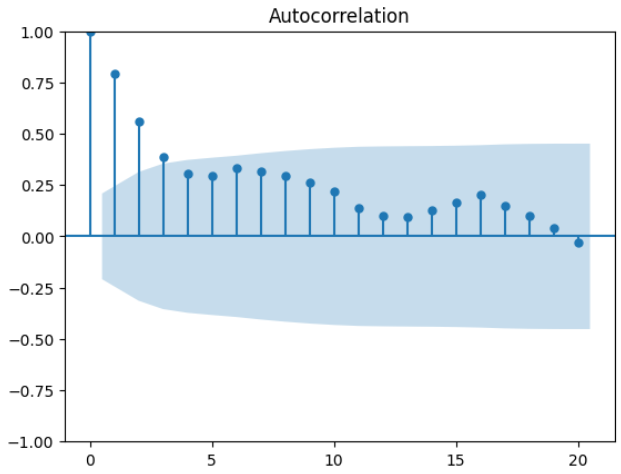

在这里插入图片描述
该图显示了前20个滞后的自相关值。该图显示不同滞后的自相关值，其中滞后在x轴上，自相关值在y轴上。该图帮助我们识别自相关值在置信区间之外的显著滞后（由阴影区域表示）。

我们可以观察到从lag=1到lag=4的显著相关性。我们使用下面提到的方法检查滞后值的相关性：

data['Temperature '].corr(data['Temperature '].shift(1))

输出

0.7997281316018658

Lag=1为我们提供了最高的相关值0.799。类似地，我们已经检查了lag= 2，3，4。对于移位设置为4，我们得到的相关性为0.31。

第3步：建模

我们将使用AutoReg模型构建一个自回归模型。

我们导入所需的库来创建自回归模型。
然后我们在训练数据上训练自回归模型。

from statsmodels.tsa.ar_model import AutoReg
from statsmodels.graphics.tsaplots import plot_acf
from statsmodels.tsa.api import AutoReg
from sklearn.metrics import mean_absolute_error, mean_squared_error# Create and train the autoregressive model
lag_order = 1 # Adjust this based on the ACF plot
ar_model = AutoReg(y_train, lags=lag_order)
ar_results = ar_model.fit()

第4步：模型评估

使用平均绝对误差（MAE）和均方根误差（RMSE）评估模型的性能。

然后，我们使用AutoReg模型进行预测，并将其标记为y_pred。
通过计算MAE和RMSE指标来评估AutoReg模型的性能。

# Make predictions on the test set
y_pred = ar_results.predict(start=len(train_data), end=len(train_data) + len(test_data) - 1, dynamic=False)
#print(y_pred)# Calculate MAE and RMSE
mae = mean_absolute_error(y_test, y_pred)
rmse = np.sqrt(mean_squared_error(y_test, y_pred))
print(f'Mean Absolute Error: {mae:.2f}')
print(f'Root Mean Squared Error: {rmse:.2f}')

输出

Mean Absolute Error: 1.59
Root Mean Squared Error: 2.30

在代码中，ar_results是拟合我们的时间序列数据的ARIMA模型。为了对测试集进行预测，我们使用ARIMA模型的预测方法。它是这样工作的：

start指定预测的起始点。在这种情况下，我们在训练数据中的最后一个数据点之后开始预测，这相当于我们测试集中的第一个数据点。
end指定预测的结束点。我们将其设置为测试集中的最后一个数据点。
dynamic=False表示我们正在使用样本外预测。这意味着每个预测点使用先前观测的真实值。这通常用于测试集上的模型评估。
预测存储在y_pred中，其中包含测试集的预测值。

第5步：可视化

根据实际温度数据可视化模型的预测。最后，使用Matplotlib库可视化AutoReg模型所做的预测。

实际预测值图：

# Visualize the results
plt.figure(figsize=(12, 6))
plt.plot(test_data["Date"] ,y_test, label='Actual Temperature')
plt.plot( test_data["Date"],y_pred, label='Predicted Temperature', linestyle='--')
plt.xlabel('Date')
plt.ylabel('Temperature')
plt.legend()
plt.title('Temperature Prediction with Autoregressive Model')
plt.show()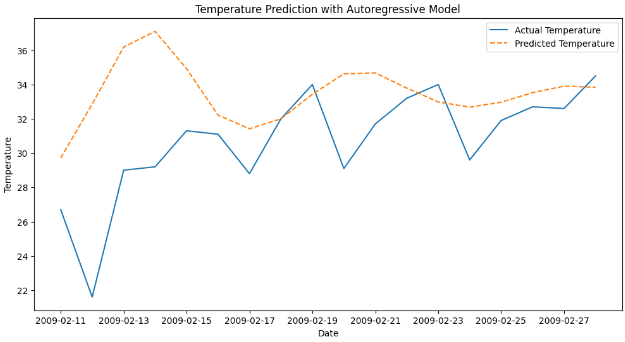

在这里插入图片描述
预测图：

# Define the number of future time steps you want to predict (1 week)
forecast_steps = 7# Extend the predictions into the future for one year
future_indices = range(len(test_data), len(test_data) + forecast_steps)
future_predictions = ar_results.predict(start=len(train_data), end=len(train_data) + len(test_data) + forecast_steps - 1, dynamic=False)# Create date indices for the future predictions
future_dates = pd.date_range(start=test_data['Date'].iloc[-1], periods=forecast_steps, freq='D')# Plot the actual data, existing predictions, and one year of future predictions
plt.figure(figsize=(12, 6))
plt.plot(test_data['Date'], y_test, label='Actual Temperature')
plt.plot(test_data['Date'], y_pred, label='Predicted Temperature', linestyle='--')
plt.plot(future_dates, future_predictions[-forecast_steps:], label='Future Predictions', linestyle='--', color='red')
plt.xlabel('Date')
plt.ylabel('Temperature')
plt.legend()
plt.title('Temperature Prediction with Autoregressive Model')
plt.show()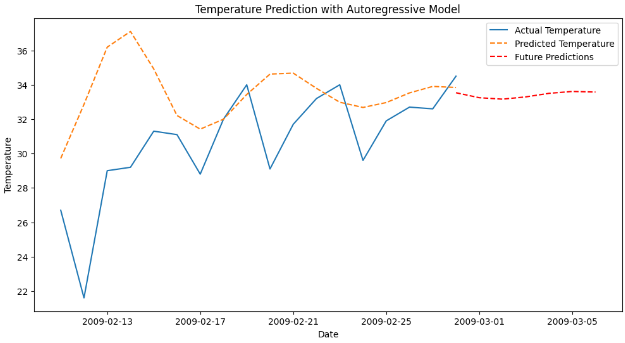

在这里插入图片描述

自回归模型的优点和缺点

自回归模型（AR模型）是一类时间序列模型，具有自己的优点和缺点。理解这些可以帮助选择何时使用它们以及何时考虑替代建模方法。

自回归模型的优点：

简单性：AR模型相对容易理解和实现。它们依赖于时间序列的过去值来预测未来值，使它们在概念上简单明了。
可解释性：AR模型中的系数有明确的解释。它们代表了过去和未来价值观之间关系的强度和方向，使我们更容易从模型中获得见解。
适用于平稳数据：AR模型适用于平稳时间序列数据。随着时间的推移，平稳数据具有稳定的统计特性，这是建立AR模型的假设。
效率：AR模型在计算上是高效的，特别是对于短时间序列或当您拥有合理数量的数据时。
建模时间模式：AR模型擅长捕捉数据中的短期时间依赖性和模式，这使得它们对短期预测很有价值。

自回归模型的缺点：

平稳性假设：AR模型假设时间序列是平稳的，这意味着其统计特性不会随时间而变化。在实践中，许多真实世界的时间序列是非平稳的，需要差分等预处理步骤。
局限于短期依赖性：AR模型不适合捕捉数据中的长期依赖性。它们主要用于建模短期时间模式。
滞后选择：在AR模型中选择适当的滞后阶数（p）可能具有挑战性。选择太少的滞后可能导致欠拟合，而选择太多的滞后可能导致过拟合。ACF和PACF图等技术用于确定滞后阶数。
对噪声的敏感性：AR模型可能对数据中的随机噪声敏感。这种敏感性可能导致过拟合，特别是在处理噪声或不规则的时间序列时。
有限的预测范围：AR模型通常不适合长期预测，因为它们被设计用于捕获短期依赖性。对于长期预测，ARIMA、SARIMA或机器学习模型等其他模型可能更合适。
数据质量依赖性：AR模型的有效性高度依赖于数据质量。离群值、缺失值或数据不规则性会显著影响模型的性能。

总结

自回归（AR）模型为分析和预测时间序列数据提供了一个强大的框架。我们探讨了AR模型的基本概念，从理解自相关到拟合模型和进行未来预测。通过生成模拟温度数据集，我们能够应用AR建模。AR模型在处理平稳时间序列数据时特别有用，因为过去的值会影响未来的观测结果。滞后阶数的选择是关键的一步，可以通过检查自相关函数（ACF）图来确定。