本文给大家带来的百面算法工程师是深度学习支持向量机的面试总结,文章内总结了常见的提问问题,旨在为广大学子模拟出更贴合实际的面试问答场景。在这篇文章中,我们还将介绍一些常见的深度学习算法工程师面试问题,并提供参考的回答及其理论基础,以帮助求职者更好地准备面试。通过对这些问题的理解和回答,求职者可以展现出自己的深度学习算法领域的专业知识、解决问题的能力以及对实际应用场景的理解。同时,这也是为了帮助求职者更好地应对深度学习算法工程师岗位的面试挑战,提升面试的成功率和竞争力。
文章目录
- 15.1 SVM
- 15.2 SVM原理
- 15.3 SVM解决问题的类型
- 15.4 核函数的作用以及特点
- 15.5 核函数的表达式
- 15.6 SVM为什么引入对偶问题
- 15.7 SVM使用SGD及步骤
- 15.8 为什么SVM对缺失数据敏感
- 15.9 SVM怎么防止过拟合
欢迎大家订阅我的专栏一起学习共同进步
祝大家早日拿到offer! let’s go
🚀🚀🚀http://t.csdnimg.cn/dfcH3🚀🚀🚀
15.1 SVM
支持向量机(Support Vector Machine,SVM)是一种机器学习算法,广泛应用于分类和回归分析中。其基本原理是找到一个最优的超平面,将不同类别的数据分开,同时最大化分类边界的间隔。SVM的核心思想是通过将低维空间的数据映射到高维空间,从而使得数据线性可分。在高维空间中,SVM寻找一个能够最大化间隔的超平面,这个超平面被称为最优超平面。
SVM在分类问题中的工作原理是将输入数据映射到一个高维特征空间中,并找到一个能够将不同类别的数据分开的超平面。为了找到这个最优超平面,SVM通过最大化间隔(样本到超平面的距离)来确保分类的鲁棒性和泛化能力。在实际应用中,由于数据通常不是线性可分的,因此SVM引入了核函数来将数据映射到高维空间,从而使得数据在高维空间中线性可分。
SVM的优点包括:
- 在高维空间中处理非线性问题:通过使用核函数,SVM可以将数据映射到高维空间,从而处理非线性问题。
- 泛化能力强:由于SVM最大化间隔,因此具有很好的泛化能力,对于新数据的分类效果较好。
- 可解释性强:最优超平面是由支持向量决定的,这些支持向量是最靠近超平面的数据点,因此SVM具有较强的可解释性。
然而,SVM也存在一些缺点,包括:
- 对参数调节和核函数的选择较为敏感。
- 训练时间较长,特别是在大规模数据集上。
- 在处理噪声较多的数据集时,可能会出现过拟合的问题。
- 用SVM解决多分类问题存在困难
总的来说,SVM是一种强大的机器学习算法,在许多分类和回归问题中都有良好的表现。
15.2 SVM原理
以下是支持向量机(SVM)的推导过程
支持向量机(SVM)推导
- 基本概念
假设我们有一个数据集 ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x n , y n ) {(x_1, y_1), (x_2, y_2), ..., (x_n, y_n)} (x1,y1),(x2,y2),...,(xn,yn),其中 x i x_i xi 是输入特征, y i y_i yi 是对应的类别标签。对于二分类问题, y i y_i yi 可以是 − 1 -1 −1 或 + 1 +1 +1。
- SVM的目标
SVM的目标是找到一个超平面,可以最大化类别之间的间隔,并且使得所有的数据点都被正确分类。超平面可以表示为 w ⋅ x + b = 0 w \cdot x + b = 0 w⋅x+b=0,其中 w w w 是法向量, b b b 是偏置项。
- 最大间隔分类器
我们定义超平面到最近的数据点的距离为间隔(margin)。最大间隔分类器的目标是最大化这个间隔。这可以形式化为以下优化问题:
maximize 2 ∥ w ∥ subject to y i ( w ⋅ x i + b ) ≥ 1 , for all i \text{maximize} \quad \frac{2}{\lVert w \rVert} \\ \text{subject to} \quad y_i(w \cdot x_i + b) \geq 1, \quad \text{for all } i maximize∥w∥2subject toyi(w⋅xi+b)≥1,for all i
这是一个凸二次优化问题。
- 对偶问题
通过拉格朗日乘子法,我们可以将原始问题转化为对偶问题。我们引入拉格朗日乘子 α i ≥ 0 \alpha_i \geq 0 αi≥0,并定义拉格朗日函数:
L ( w , b , α ) = 1 2 ∥ w ∥ 2 − ∑ i = 1 n α i [ y i ( w ⋅ x i + b ) − 1 ] L(w, b, \alpha) = \frac{1}{2}\lVert w \rVert^2 - \sum_{i=1}^{n} \alpha_i [y_i(w \cdot x_i + b) - 1] L(w,b,α)=21∥w∥2−i=1∑nαi[yi(w⋅xi+b)−1]
然后对 w w w 和 b b b 求偏导并令其等于零,得到:
w = ∑ i = 1 n α i y i x i ∑ i = 1 n α i y i = 0 w = \sum_{i=1}^{n} \alpha_i y_i x_i \\ \sum_{i=1}^{n} \alpha_i y_i = 0 w=i=1∑nαiyixii=1∑nαiyi=0
将这些结果代入拉格朗日函数,我们得到对偶问题:
maximize W ( α ) = ∑ i = 1 n α i − 1 2 ∑ i , j = 1 n α i α j y i y j x i ⋅ x j subject to α i ≥ 0 , ∑ i = 1 n α i y i = 0 \text{maximize} \quad W(\alpha) = \sum_{i=1}^{n} \alpha_i - \frac{1}{2} \sum_{i,j=1}^{n} \alpha_i \alpha_j y_i y_j x_i \cdot x_j \\ \text{subject to} \quad \alpha_i \geq 0, \quad \sum_{i=1}^{n} \alpha_i y_i = 0 maximizeW(α)=i=1∑nαi−21i,j=1∑nαiαjyiyjxi⋅xjsubject toαi≥0,i=1∑nαiyi=0
这是一个凸二次优化问题,其解决方案给出了最优的超平面。
- 从对偶问题中得到分离超平面
通过解决对偶问题,我们得到了一组拉格朗日乘子 α i ∗ \alpha_i^* αi∗。然后,我们可以使用它们来计算权重向量 w w w:
w = ∑ i = 1 n α i ∗ y i x i w = \sum_{i=1}^{n} \alpha_i^* y_i x_i w=i=1∑nαi∗yixi
并且选择任意一个支持向量 x i x_i xi 来计算偏置项 b b b:
b = y i − w ⋅ x i b = y_i - w \cdot x_i b=yi−w⋅xi
- 非线性SVM
对于非线性问题,我们可以使用核函数将输入空间映射到更高维的特征空间。这样,我们就可以在特征空间中找到一个线性超平面来分隔数据。
支持向量机是一种强大的分类器,通过最大化间隔来优化超平面位置,从而提高了分类的鲁棒性。通过解决对偶问题,我们可以得到优雅的解决方案,并且通过核函数,SVM可以处理非线性问题。
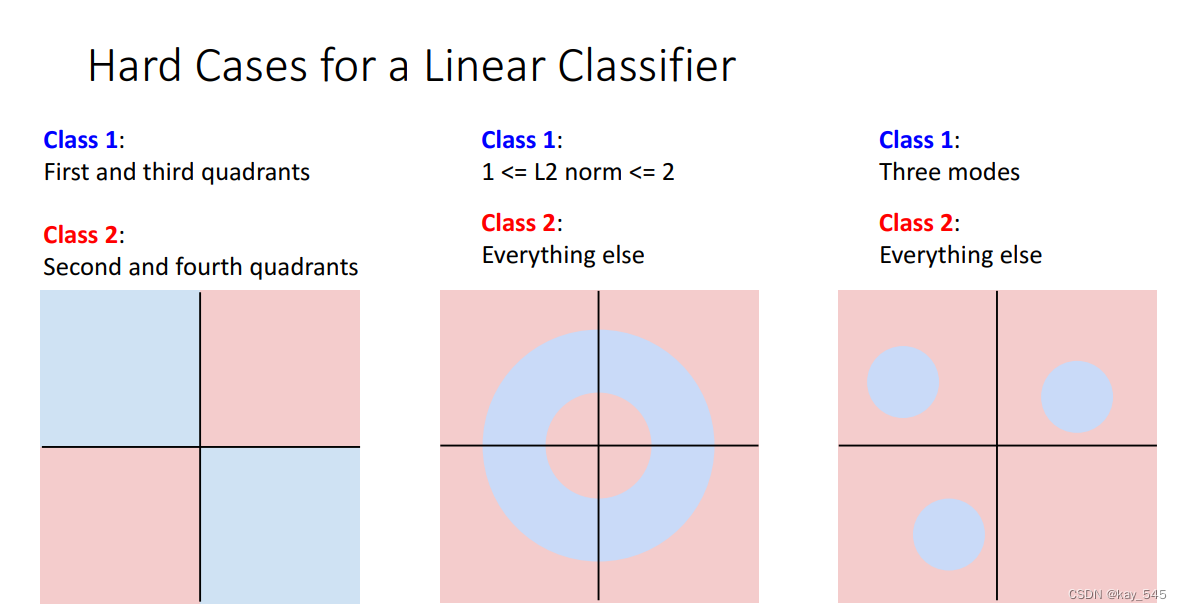
15.3 SVM解决问题的类型
支持向量机(SVM)是一种非常强大的监督学习算法,它在许多问题领域都有广泛的应用。以下是SVM能够解决的一些主要问题:
-
二分类问题:SVM最初是用于二分类问题的,它可以有效地将数据划分为两个类别,并找到最优的超平面以实现最大间隔分类。
-
多分类问题:虽然SVM最初是为二分类设计的,但可以使用一些技巧来扩展它以解决多分类问题,例如一对一(One-vs-One)或一对其他(One-vs-Rest)策略。
-
线性可分问题:当数据可以通过一个超平面完全分割成两个类别时,SVM表现最好。
-
线性不可分问题:通过使用核函数,SVM可以处理线性不可分的情况,将数据映射到更高维的特征空间中,使其变得线性可分。
-
回归问题:SVM也可以用于解决回归问题。通过引入一个适当的损失函数和辅助变量,SVM可以拟合数据并找到一个最优的超平面,以尽量减小预测值与真实值之间的误差。
-
异常检测:SVM在异常检测中也有应用。它可以识别与其他样本不同的样本,这些样本可能是异常值或异常行为。
-
文本分类:SVM在文本分类问题中也非常常见,例如垃圾邮件检测、情感分析等。
-
图像分类:SVM也可以用于图像分类任务,例如图像识别、人脸识别等。
总的来说,SVM是一种多功能的机器学习算法,适用于多种类型的问题,尤其在高维空间中或者数据量较小的情况下表现良好。
15.4 核函数的作用以及特点
支持向量机(SVM)通过核函数将输入空间映射到更高维的特征空间,这使得SVM能够解决非线性分类问题。核函数在SVM中具有重要的作用和特点,让我们来详细看看:
作用:
-
处理非线性问题:核函数允许SVM在高维特征空间中构建线性分割超平面,即使在原始输入空间中不存在线性分割的情况下也能有效分类。
-
提高分类性能:通过核技巧,SVM可以利用更复杂的超平面进行分类,这通常可以提高分类器的性能。
-
减少特征工程的需求:在不使用核函数时,为了使数据线性可分,通常需要手动进行特征工程来提取更高维度的特征。而使用核函数,可以直接在原始数据上进行操作,减少了特征工程的需求。
-
处理高维数据:核函数使得SVM在高维特征空间中能够更好地处理数据,这在许多现实世界的问题中非常有用,例如图像分类或自然语言处理。
特点:
-
计算高效性:良好的核函数可以大幅提高SVM的计算效率。一些核函数,如线性核函数和径向基函数(RBF)核函数,计算效率较高,适用于大规模数据集。
-
拟合能力:不同的核函数对数据的拟合能力不同。一些核函数可能对某些类型的数据更适用,因此在选择核函数时需要考虑数据的特点和问题的需求。
-
通用性:一些核函数在不同的问题领域中都表现良好,具有较强的通用性,例如RBF核函数。而有些核函数可能更适合特定类型的数据或特定的问题。
-
超参数调节:核函数通常有一些超参数需要调节,例如RBF核函数的 γ \gamma γ 参数。调节这些超参数可以影响SVM的性能和泛化能力,因此需要进行适当的调优。
总的来说,核函数是SVM的关键组成部分,它们允许SVM在高维空间中进行有效的分类,并且可以适应各种类型的数据和问题。选择合适的核函数以及调节相应的参数对于SVM的性能和表现至关重要。
15.5 核函数的表达式
当谈到支持向量机(SVM)时,有几种常见的核函数,每种核函数都有其独特的特点和适用范围。以下是一些常见的核函数及其表达式,以Markdown格式列出:
| 核函数名称 | 表达式 |
|---|---|
| 线性核函数 (Linear Kernel) | K ( x , x ′ ) = x T x ′ K(x, x') = x^T x' K(x,x′)=xTx′ |
| 多项式核函数 (Polynomial Kernel) | K ( x , x ′ ) = ( x T x ′ + c ) d K(x, x') = (x^T x' + c)^d K(x,x′)=(xTx′+c)d |
| 高斯核函数 (Gaussian Kernel, RBF) | K ( x , x ′ ) = e − γ ∣ x − x ′ ∣ 2 K(x, x') = e^{-\gamma |x - x'|^2} K(x,x′)=e−γ∣x−x′∣2 |
| Sigmoid核函数 (Sigmoid Kernel) | K ( x , x ′ ) = tanh ( α x T x ′ + c ) K(x, x') = \tanh(\alpha x^T x' + c) K(x,x′)=tanh(αxTx′+c) |
这些是最常见的核函数之一。线性核函数适用于线性可分的情况,多项式核函数和高斯核函数可以处理非线性问题,而Sigmoid核函数有时也被用于一些特定的情况。每种核函数都有其自己的一组参数,如多项式核函数中的 (c) 和 (d),以及高斯核函数中的 (\gamma)。选择合适的核函数和参数对于SVM的性能和泛化能力至关重要。
15.6 SVM为什么引入对偶问题
SVM 引入对偶问题是为了解决原始问题在优化过程中可能面临的一些挑战,以及为了更好地理解和优化问题。
主要原因包括:
-
计算效率:原始问题通常涉及对权重向量和偏置项的优化,这样的问题通常是一个带有约束的凸二次规划问题。解决这样的问题可能需要复杂的数值优化技术,计算量较大。而对偶问题通过引入拉格朗日乘子,可以将原始问题转化为一个更简单的形式,使得更容易求解。
-
理论分析:对偶问题在理论分析上更容易处理。通过对对偶问题进行分析,我们可以得到一些关于原始问题的性质和解的性质的洞见,例如 KKT 条件。这有助于更深入地理解问题的本质和解的特性。
-
核方法的应用:对偶问题的形式使得核方法(kernel methods)更容易应用。在对偶问题中,内积的计算被表示为核函数的形式,这使得我们可以将数据映射到更高维的特征空间中进行处理,而无需显式地计算出映射后的特征向量。
-
解决线性不可分问题:对偶问题形式使得引入核函数变得自然和方便。通过核函数,我们可以将原始问题中的特征空间映射到更高维的空间中,从而使得线性不可分的问题变为线性可分的问题。
综上所述,引入对偶问题能够简化优化问题的求解过程,同时也有助于更深入地理解问题的本质和应用核方法进行高效的非线性分类。
15.7 SVM使用SGD及步骤
支持向量机(SVM)可以用随机梯度下降(SGD)进行训练。SGD是一种优化算法,用于寻找损失函数的最小值,其每次更新参数时只使用一个样本或一小批样本,而不是全部数据。虽然SGD通常用于训练大规模数据集上的模型,但也可以应用于SVM的优化过程中。
SGD在SVM中的应用通常涉及以下几个步骤:
-
定义损失函数:首先需要定义SVM的损失函数,通常使用hinge loss(合页损失)。
-
随机抽样:从训练数据中随机抽取一个样本或一小批样本。
-
计算梯度:根据当前参数和选取的样本,计算损失函数关于参数的梯度。
-
更新参数:使用计算得到的梯度来更新参数,减小损失函数的值。
-
迭代:重复执行2至4步,直到达到停止条件(例如达到最大迭代次数或损失函数收敛)。
虽然SGD可以用于SVM的训练,但与传统的优化方法(如序列最小优化算法)相比,它可能收敛速度较慢,并且需要更仔细地调整学习率和其他超参数以获得良好的性能。此外,SGD在处理非线性核函数时可能需要更多的技巧和调整。
总的来说,尽管SVM可以使用SGD进行训练,但在实践中可能需要更多的调优和注意事项,以确保收敛性和性能。
15.8 为什么SVM对缺失数据敏感
支持向量机(SVM)对于缺失数据的敏感性主要源自其优化目标和核函数的计算方式。
-
优化目标的定义:SVM的优化目标是找到一个最大间隔超平面,使得所有数据点都被正确分类。如果数据中存在缺失值,这可能导致超平面的位置被不完整的数据影响,从而使得最终分类效果受到影响。
-
核函数的计算:在使用核函数时,SVM通常会涉及计算数据点之间的内积,例如在高斯核函数中。如果存在缺失值,计算数据点之间的内积将会受到影响,因为无法直接计算缺失值的内积。即使在填充缺失值后,由于填充的值可能并不准确或合理,计算出的内积也可能不具备合适的特征。
-
缺失数据处理:在实践中,SVM通常要求输入数据是完整的,因为SVM本身并不具备处理缺失值的机制。因此,处理缺失数据可能需要先进行填充或者删除操作,这可能导致数据信息的丢失或者不准确性。
综上所述,SVM对于缺失数据敏感是由于其对数据完整性的要求以及核函数计算的特性。在应用SVM时,需要注意处理缺失数据的方法,以确保模型的性能和稳定性。
15.9 SVM怎么防止过拟合
支持向量机(SVM)是一种强大的分类器,但同样也容易受到过拟合的影响。以下是一些防止SVM过拟合的方法:
-
正则化参数调节:SVM有一个正则化参数 ( C ),它控制着模型的复杂度。增加 ( C ) 的值会导致模型更倾向于对训练数据拟合,可能会增加过拟合的风险。因此,可以通过交叉验证等方法来调节 ( C ) 的值,以避免过拟合。
-
数据预处理:数据预处理是防止过拟合的重要步骤之一。包括特征缩放、特征选择和降维等技术。通过对数据进行预处理,可以减少特征的数量,降低模型的复杂度,从而降低过拟合的风险。
-
交叉验证:使用交叉验证可以评估模型的泛化能力,并且选择合适的超参数。通过将数据划分为训练集和验证集,并在不同的训练集上训练模型,然后在验证集上评估模型性能,可以更好地了解模型在未见过数据上的表现。
-
核函数选择:选择合适的核函数也是防止过拟合的重要因素。一些核函数,如高斯核函数(RBF),可能更容易导致过拟合,因为它们有更多的自由度。在选择核函数时,应该根据数据的特性和问题的需求进行权衡。
-
减少特征维度:如果特征空间过于庞大,可能会增加过拟合的风险。因此,可以通过特征选择、降维或者正则化等方法来减少特征维度,从而降低模型的复杂度。
-
集成学习方法:使用集成学习方法,如随机森林或梯度提升树等,可以降低单个模型过拟合的风险。通过组合多个模型的预测结果,可以减少单个模型的偏差和方差,提高整体的泛化能力。





![[iOS]从拾遗到Runtime(上)](https://img-blog.csdnimg.cn/direct/ecdc6b1172bd44518e275f37c6844f24.png)