LeetCode：116.填充每个节点的下一个右侧节点指针
题目：

示例：

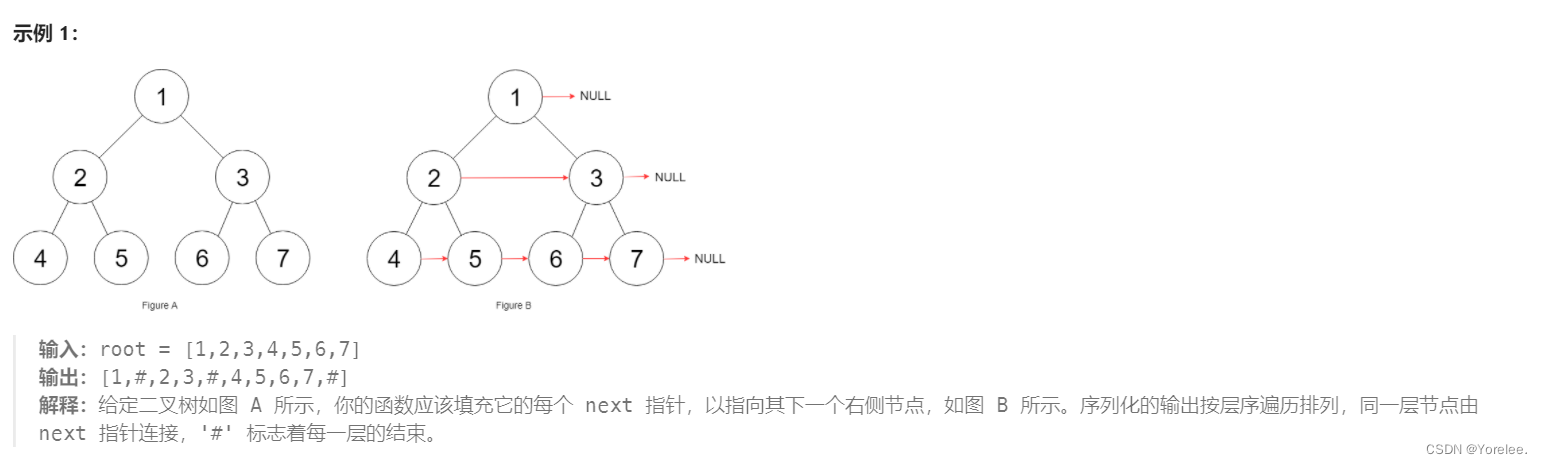
分析题意容易关注到只需要将每层结点连接起来，因此我们只需要把每层结点求出来即可，即使用层次遍历。

1.层次遍历

使用队列方式的层序遍历，将一层的结点进行连接。

时间复杂度：$O(n)$

空间复杂度：$O(n)$

class Solution {
public:Node* connect(Node* root) {if(!root) return NULL;queue<Node * > q;q.push(root);while(!q.empty()){int size = q.size();for(int i = 0;i < size;++i){if(q.front()->left)q.push(q.front()->left);if(q.front()->right)q.push(q.front()->right);Node * cur = q.front();q.pop();if(!q.empty() && i != size - 1)cur->next = q.front();}}return root;}
};

---

2.使用next层序遍历

进一步思考我们可以发现，由于我们将每层连接起来了，因此我们可以直接使用next指针实现层序遍历的方法！

时间复杂度：$O(n)$

空间复杂度：$O(1)$

class Solution {
public:Node* connect(Node* root) {Node* start = root;while(start != nullptr){Node * floor = start;start = start->left;//start指向下一层的开始for(;floor != nullptr;floor = floor->next){//遍历该层if(floor->left){//是否有儿子floor->left->next = floor->right;if(floor->next)floor->right->next = floor->next->left;}}}return root;}
};

3.递归方法

根据进阶提示，也能使用递归方法，但是感觉递归的方法很难想。
主要体现在：

单子树递归肯定无法实现，两颗子树之间的连接，因此我们需要寻求更好的递归函数。

受到力扣hot100：101. 对称二叉树的启发，我们可以尝试使用双指针将两颗子树连接起来。

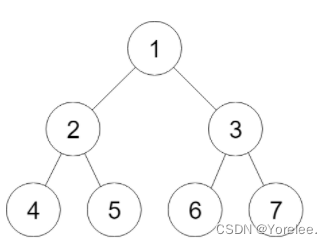
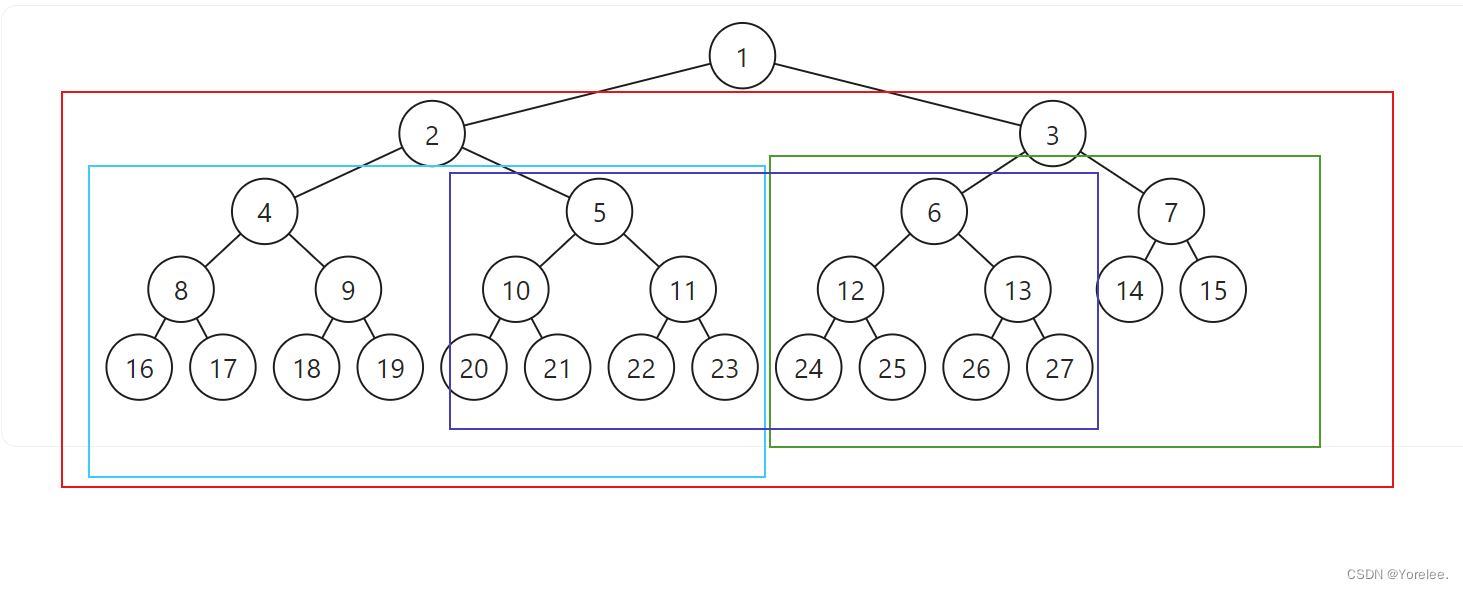
将整棵树画出来，从上向下看，我们如果使用双指针p和q，如果要连接该层（比如2连向3），则先将p连向q，那么我们定义函数的功能是让p连向q。

然后由于我们递归向下，所以递归方式要求不同子树之间也需要连接，则要满足：

• p的子树要连起来，所以递归调用函数传入p->left和p->right
• q的子树要连起来，所以递归调用函数传入q->left和q->right
• p和q之间要连起来，所以递归调用函数传入p->right和q->left

因此我们就实现了这个递归：

    void connect_node(Node * & p,Node * & q){if(!p || !q) return;p->next = q;//连接p和qconnect_node(p->right,q->left);//中间需要连起来connect_node(p->left,p->right);//左子树需要连起来connect_node(q->left,q->right);//右子树需要连起来return;}

---

时间复杂度：$O(n)$

空间复杂度：$O(1)$ （根据题设知忽略递归栈空间开销）

class Solution {
public:Node* connect(Node* root) {if(!root) return NULL;connect_node(root->left,root->right);return root;}void connect_node(Node * & p,Node * & q){if(!p || !q) return;p->next = q;connect_node(p->right,q->left);connect_node(p->left,p->right);connect_node(q->left,q->right);return;}
};