1. 环形链表1. - 力扣(LeetCode)



要解决这道题,我们首先要挖掘出带环的链表与不带环的链表之间的差别。
以此,才能设计出算法来体现这种差别并判断。
二者最突出的不同,就是不带环的链表有尾结点,也就是说在访问到某个结点时,其next指针可能为NULL。
而带环的链表则没有尾结点,负责访问链表的指针进入环以后,就会一直在环中转圈。
但是,仅靠这个,我们很难解决这个问题。
按以上得到的信息来说,我们会尝试去1. 检查该链表是否有尾结点,或者2. 检查有无结点被重复访问。
对于第一种思路,很明显行不通,因为在检查一个带环的链表时,我们会一直访问不到尾结点,但我们也无法找到确切的指标来证明该链表确实没有尾结点。
对于第二种思路,一般来说,我们会想到将已访问过的结点的地址保存起来,每访问一个结点,我们就检查已保存的地址中是否有与新结点地址相同的地址。
第二种思路没有任何问题,确实可以顺利解决这个问题,那么我们来看看进阶要求。
![]()
很明显,第二种思路写出的算法的时间复杂度为O(n!),空间复杂度为O(n)。
也就是说还有更妙的办法,或者说带环链表和不带环链表之间还有更加值得利用的区别。
仔细观察就能发现,带环会改变环中结点之间的相对关系。
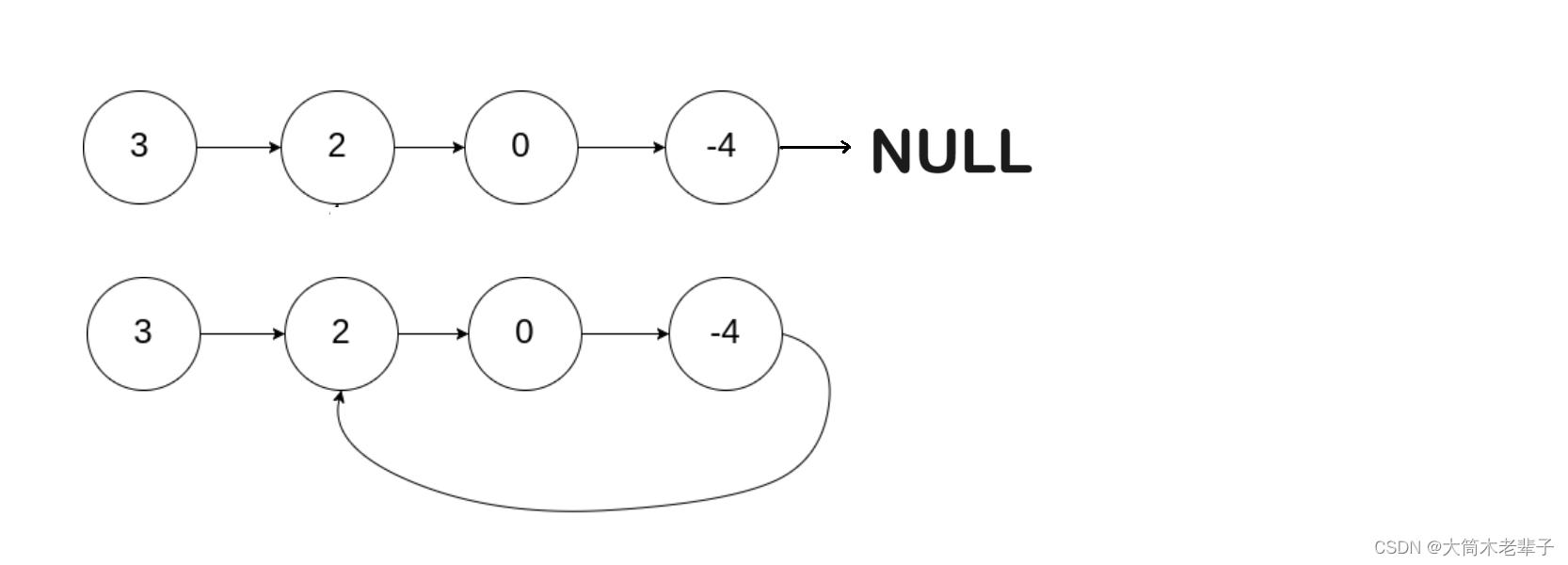
当链表不带环时,我们可以肯定地说:值为2的结点在值为-4的结点之前。
但是,当链表带环时,我们却可以认为值为-4的结点在值为2的结点之前,因为值为-4的结点的next指针指向的是值为2的结点。
也就是说,带环改变了环中结点之间的前后相对关系。
那么,我们如何使得这种差异体现出来呢?
这使得我们想到快慢指针:
假设快慢指针的都从头结点开始移动。
当链表不带环时,快慢指针一旦分开便再无相遇的可能;
当链表带环时,由于环中结点的相对关系被改变,在快慢指针都进入环之后,原本在前的快指针可以认为是在慢指针之后,那么快指针就会不断追击慢指针,最终二者可能相遇。
但是,我们如何确保快指针最后一定会追上慢指针呢?
在追击过程中,二者每次移动,它们之间的距离的减少量就是二者的速度之差。
由于在慢指针刚进入环时,二者之间的距离一定为整数,所以当二者的速度之差为1时,它们就必定相遇。
依据此思路,我们可以设计出如下的算法:
typedef struct ListNode ListNode;bool hasCycle(struct ListNode *head) {ListNode* slow = head;ListNode* fast = head;while(fast && (fast->next)){fast = fast->next->next;slow = slow->next;if(fast == slow)return true;}return false;
}很明显,该算法的时间复杂度为O(n),空间复杂度只有O(1),满足的进阶的要求并明显减小了时间复杂度。
2. 数学分析
完成这道题还不足以让你通过面试,接下来面试官可能会问你:
1. 二者为什么一定会相遇呢?
2. 慢指针每次前进一个结点,快指针每次前进三个结点可以吗?四或五个结点呢?
第一个问题我们在解题的过程中就已经解决,你只要将思路清晰地阐述即可。
对于第二个问题,要让面试官刮目相看,我们自然不满足于只解决给出的三种情况(对具体情况单独分析也挺麻烦的),我们会尝试给出判断可行的数学公式。
我们假设:
1. 环的周长为c(环有c个结点)。
2. 当慢指针刚进入环时,快指针已经在环中移动的长度为L。
3. 快指针的速度为k(每次移动k个结点)。
4. 慢指针进入环之后,移动n次时与快指针相遇。
将进入环的第一个结点标记为下标0,随后结点的下标依次递增,直到再次遇到下标为零的结点。

二者相遇时,快慢指针的位置是相同的。
据此,当二者相遇时,一定满足这个表达式:(nk + L) % c = n % c
假设相遇时,快指针比慢指针多走了m圈,则有:nk + L = n + mc
移项可得:n = (mc - L) / (k - 1)
由于n为整数,所以,如果存在m使得(mc - L) % (k - 1) = 0,我们就可以认为二者一定会相遇。
很明显,当k = 2时,上式一定成立(任何整数都可以整除1),这也就验证了我们之前的结论。
而当k > 2时,上式能否成立则受到c与L的影响,无法保证一定成立。
3. 环形链表2. - 力扣(LeetCode)

也就是在刚才的基础之上,要求我们求出环中的第一个结点。
这个时候,我们之前想到的第一种思路似乎就能派上用场了:如果找到了重复访问的结点,直接返回该结点的地址即可。
但是,这道题依然有同样的进阶要求:
![]()
同样的要求,也就是在提示我们这道题的最佳思路一定是建立在第一题的解法之上。
那么在第一题判断该链表有环之后,我们要如何找到环中第一个结点呢?
不妨先考虑一下,当快慢指针相遇时,二者在哪个位置。
当慢指针刚好进入环时,快指针的坐标为L % c。
按照快指针追击慢指针的角度来看,快慢指针之间相距的距离为c - (L % c)。
每移动一次,二者之间的距离会缩短1,那么二者共会移动c - (L % c)次。
所以,最终慢指针的坐标会停留在c - (L % c)处,也即二者相遇时的坐标。
此时,慢指针要再次到达下标为0的结点(环中第一个结点),需要再移动(L % c)次。
注意到,L = (L % c) + xc(x为整数)。
也就是说,让慢指针移动L次,其也依然会到达下标为0处(多绕x圈)。
可是,此时,我们怎么知道L是多少呢?
仔细观察会发现,头结点到环中第一个结点的距离恰好就是L。
因为快指针的速度是慢指针的两倍,所以,在进环之前,头结点到慢指针的距离与慢指针到快指针的距离是相等的。
在慢指针恰好进入环时,头结点到环中第一个结点的距离就等于慢指针到快指针的距离,即L。
所以,我们只需要让头结点处的指针和相遇处的指针同时开始移动(每次一个结点),最终就会在下标为0的结点处相遇。
依据这个思路,我们可以写出如下代码:
typedef struct ListNode ListNode;struct ListNode *detectCycle(struct ListNode *head) {ListNode* slow = head;ListNode* fast = head;while(fast && (fast->next)){fast = fast->next->next;slow = slow->next;if(fast == slow){ListNode* meet = slow;while(meet != head){meet = meet->next;head = head->next;}return meet;}}return NULL;
}4. 结语
如果你在面试中遇到了这道题并清晰流畅地答出了本文的内容,那么你的面试就稳了一半了。
如果觉得写的不错就三连支持一下吧!
加纳……