(代数:解一元二次方程)可以使用下面的公式求一元二次方程 ax2+bx+c0 的两个根:

 b2-4ac 称作一元二次方程的判别式。如果它是正值,那么一元二次方程就有两个实数根。
如果它为 0，方程式就只有一个根。如果它是负值，方程式无实根。
编写程序，提示用户输入 a、b和c的值，并且显示基于判别式的结果。如果这个判别式
为正,显示两个根。如果判别式为0,显示一个根。否则,显示“Theequationhasnorealroots
(该方程式无实数根)。
注意:可以使用 Math.pow(x，0.5)来计算√x，下面是一些运行示例。
Entera, b, c:1.031
Theequationhastworoots-0.381966and-2.61803
Entera, b, c:12.01
Theequationhasoneroot-1
Enteratbtc:123
Theequationhasnorealroots

package myjava;
import java.math.*;
import java.util.Scanner;
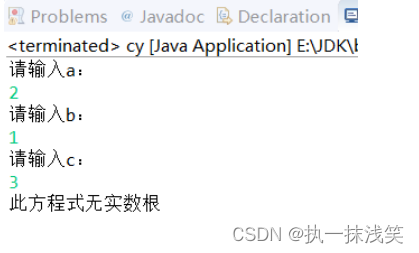
public class cy {public static void main(String[]args){double a,b,c,d,r1,r2;Scanner input = new Scanner(System.in);System.out.println("请输入a：");a=input.nextDouble();System.out.println("请输入b：");b=input.nextDouble();System.out.println("请输入c：");c=input.nextDouble();d=Math.pow(b*b-4*a*c, 0.5);r1=(-b+d)/2*a;r2=(-b-d)/2*a;	if(d>0)System.out.println("两个根为："+r1   +r2);else if(d==0)System.out.println("一个根为"+r1);elseSystem.out.println("此方程式无实数根");}
}

运行结果：