算法设计与分析例题解答解空间与搜索

1.请画出用回溯法解n=3的0-1背包问题的解空间树和当三个物品的重量为{20, 15, 10}，价值为{20, 30, 25}，背包容量为25时搜索空间树。

答：

解空间树：

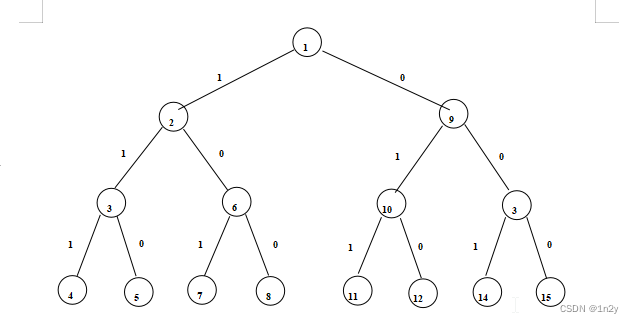
搜索空间树：

考虑用分支限界解0-1背包问题

给定n种物品和一背包。物品i的重量是wi，其价值为vi，背包的容量为C。问应如何选择装入背包的物品，使得装入背包中物品的总价值最大?

示例：n=3, C=30, w={16, 15, 15}, v={45, 25, 25}

求：1、问题的解空间树

2、约束条件

2、如何剪枝？

问题的解空间树：

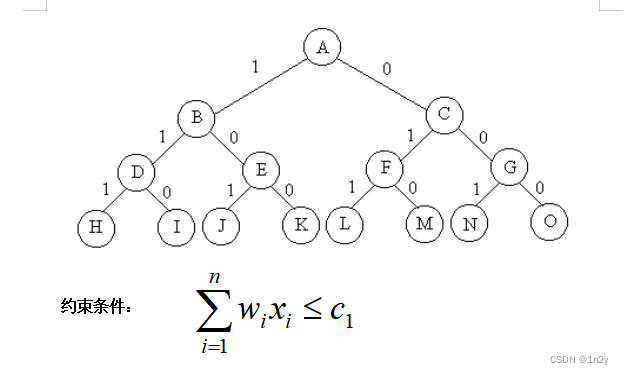
设r是当前尚未考虑的剩余物品价值总和；Cv是当前价值；bestv是当前最优价值。

当r＋Cv≤bestv时，可剪去右子树。

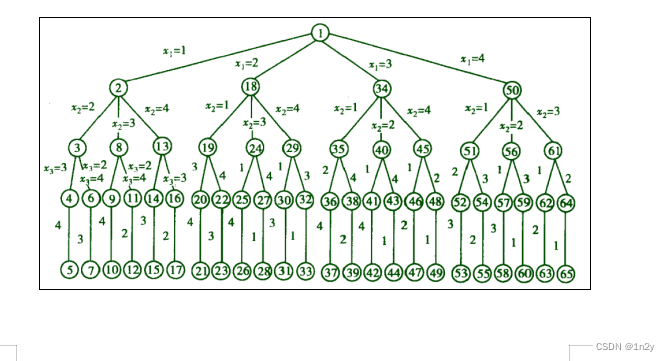
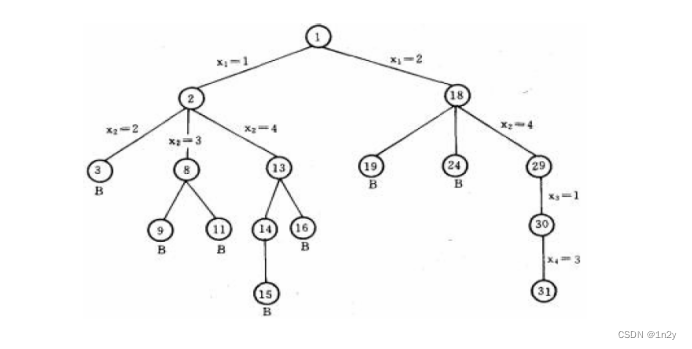
3.请画出用回溯法解4皇后问题的解空间树和搜索空间树：

考虑使用动态规划方法求解下列问题：

01背包数据如下表，求：能够放入背包的最有价值的物品集合。

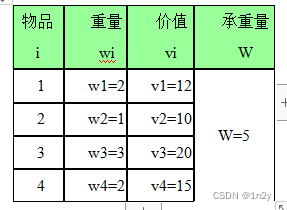
如设： V(i, j) —— 前 i 个物品中能够装入承重量 j 的背包中的最大总价值。请将如下递推式填写完整：

V(0, j) = 0（0个物品），V(i, 0) = 0（承重量0）

V(i, j) = V(i-1, j) 第 i 个物品不能装入， j < wi （超重）

V(i, j) = max { , } j > wi （不超重）

i在最优子集中 i不在最优子集中

自底向上：按行或列填写下表。

V	j=0	1	2	3	4	5
i=0	0	0	0	0	0	0
1	0
2	0
3	0
4	0

答：

V(0, j) = 0（0个物品），V(i, 0) = 0（承重量0）

V(i, j) = V(i-1, j) 第 i 个物品不能装入， j < wi （超重）

V(i, j) = max { vi + V(i-1,j-wj) , V(i-1, j) } j > wi （不超重）

i在最优子集中 i不在最优子集中

V	j=0	1	2	3	4	5
i=0	0	0	0	0	0	0
1	0
2	0
3	0
4	0

V	j=0	1	2	3	4	5
i=0	0	0	0	0	0	0
1	0	0	12	12	12	12
2	0	10	12	22	22	22
3	0	10	12	22	30	32
4	0	10	15	25	30	37

考虑在序列A[1..n]中找最大最小元素的问题。一个分治算法描述如下：如果n≤2 就直接求解。否则，将序列等分成两个子序列A[1..n/2]和A[n/2+1..n]，分别找出这两子序列的最大最小元素x1,y1 和x2,y2；然后据此求出A[1..n]的最大元素x=max{x1,x2}及最小元素y=min{y1,y2}。请给出该算法计算时间T(n)满足的递归方程，并解方程来确定算法的时间复杂度。假定n=2k（k 为正整数）。

答：

算法时间复杂度满足如下递归方程：

T(n)=2T(n/2)+2（n>2）；T(2)=1。

因为 n=2 k（k 为正整数），所以，

T(n)= T(2 k)= 2T(2 k-1)+2= 22T(2 k-2)+ 22+2

⋯

= 2k-1T(2)+ 2k-2+⋯+23+22+2

= 2k-1+⋯+23+22+2。因此，T(n)=Q(n)。