图搜索算法 - 拓扑排序

相关文章：
数据结构–图的概念
图搜索算法 - 深度优先搜索法（DFS）
图搜索算法 - 广度优先搜索法（BFS）

拓扑排序

概念

几乎所有的工程都可分为若干个称作活动的子工程，而这些子工程之间，通常受着一定条件的约束,如其中某些子工程的开始必须在另一些子工程完成之后。对整个工程和系统，人们关心的是两个方面的问题：一是工程能否顺利进行；二是估算整个工程完成所必须的最短时间。这样两个问题都是可以通过对有向图进行拓扑排序和关键路径操作来解决的。当然这里说的工程，泛指一切的项目工程，如指令调度，数据序列化，软件安装包依赖关系，代码编译任务顺序等。

拓扑排序是对项目工程的排序，那么先来构建一个项目，比如这个项目制作番茄炒蛋，如图所示。
在这里插入图片描述
对一个有向无环图G进行拓扑排序，是将G中所有结点排成一个线性序列，使得图中任意一对结点u和v，u在线性序列中总是出现在v之前。如上面做菜顺序0-1-2-3-4-5-9-6-7-8，也可以0-3-2-1-4-5-9-6-7-8这样，都满足拓扑次序(Topological Order)，也就是番茄总是要洗了再切，番茄要切成小块再炒，不能整个炒，这样的顺序不会改变，这简称拓扑序列。简单的说，由某个集合上的一个偏序得到该集合上的一个全序，这个操作称之为拓扑排序。

注意：偏序是指集合中仅有部分元素可比较大小（或先后），全序是指集合中所有元素可比较大小（或先后）。

原理

拓扑排序算法是基于深度优先搜索（以下简称DFS）的基础上做调整的，首先查看例子用DFS计算是怎样的结果，从结点【1】开始继续搜索，结果是0-1-4-7-8-2-5-9-3-6。显然这是不是拓扑排序的结果，因此要略为修改DFS。从一个结点出发，DFS是马上输出再递归进入相邻结点，这是不适合拓扑排序。这里应该先访问相邻的结点，若还有相邻结点，继续深入下一个结点，当所有相邻的结点都进入栈后，才把该结点推入栈，以下手动模拟此运算过程。

（1）首先初始化列表【visited】全部为【False】，所有结点刚开始都是未访问以及临时栈【stack】为空。然后从结点【0】开始，然后发现有3个结点，然后继续访问结点【1】，同理一直深入访问结点【4】、结点【7】和结点【8】，到这里没有发现相邻结点，那边我们把结点【8】入栈，然后回退到结点【7】，同样它也没有其他相邻结点，同样也入栈，同理结点【4】和结点【1】也一起入栈，如表所示。
在这里插入图片描述
（2）回到结点【0】，发现还有相邻结点【2】和【3】，然后我们访问结点【2】，同样一层层深入结点，直到结点【8】，由于它已经访问过了，所以不需要再次放到栈里面。然后回退到上一个结点【9】就可以放到栈里面，同理结点【5】和【2】也一起入栈，如表所示。
在这里插入图片描述
（3）继续访问未访问结点【3】，然后进入结点【6】，然后再想进一步访问结点【7】，发现它也在栈中，所以可以停止递归，把结点【6】推入栈，再把结点【3】入栈，这时候结点【0】所有相邻结点也访问完，也可以把它入栈，如表所示。
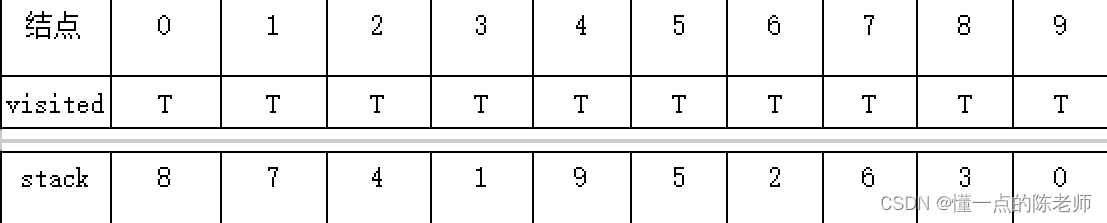
在这里插入图片描述
（4）这时候从栈中输出结果，从顶部结点开始结构为0-3-6-2-5-9-1-4-7-8，符合了拓扑排序的要求。
在编写代码前，先来分析算法的复杂度，如果图中有N个结点，E条边，在拓扑排序的过程中，因为复用【Graph】类，则使用邻接列表来表示图，所以查找所有结点的邻接结点所需时间为O(N)，访问结点的邻接点所花时间为O(E)，总的时间复杂度为O(N+E)。空间复杂度为递归深度，极限情况就是结点总数，则为O(Ｎ)。

class Graph(): """图类"""def __init__(self): self.graph = {}  # 初始化图的邻接列表def add_edge(self,u,v): if v:point = self.graph.get(u) # 尝试获取结点uif point:point.append(v)       # 若存在直接添加u-v的边else:self.graph[u] = [v]   # 若不存在，则先初始化u结点，然后再添加u-v的边else:self.graph[u] = list()  # 如果v没有值，添加一个空列表class GraphTopological(Graph):"""解决拓扑排序问题"""def topological_sort_util(self, v, visited, stack): visited[v] = True       # 该结点变为已访问for i in self.graph[v]: if visited[i] == False: # 结点未访问递归调用函数self.topological_sort_util(i, visited, stack) # 相邻结点都访问结束后，把该结点放到栈中stack.insert(0,v)  # 把新入栈元素放在表头def topological_sort(self):# 拓扑排序主程序visited = {}   # 初始化参数是否已经访问stack = [] # 初始化参数，用列表表示临时栈为空for key in self.graph.keys():visited[key] = False     # 值为未访问状态for node in self.graph.keys(): # 遍历所有结点 if visited[node] == False: # 结点是否已经访问self.topological_sort_util(node, visited, stack) # 递归进入结点print(stack) #把栈保存结果输出

创建【TopologicalGraph】类继承上面【Graph】类，复用构成邻接列表的过程。然后用列表构成栈，把递归结果保存在列表中，最后从栈表头开始输出结果便是拓扑排序的结果，现在用例子来测试结果是否符合预期。

g = GraphTopological() 
g.add_edge(0, 1) # 录入图的边
g.add_edge(0, 2) 
g.add_edge(0, 3) 
g.add_edge(1, 4) 
g.add_edge(2, 5) 
g.add_edge(3, 6)
g.add_edge(4, 7)
g.add_edge(5, 9)
g.add_edge(6, 7)
g.add_edge(7, 8)
g.add_edge(8, None)
g.add_edge(9, 8)
g.topological_sort() # 输出:[0, 3, 6, 2, 5, 9, 1, 4, 7, 8]