AVL 树的理解和简单实现

1. AVL 树

1.1. AVL 树的概念

1.2. AVL 树的性质

2. AVL 树的框架如下

2. AVL树的插入

2.1. 平衡因子的更新

2.2.1. 平衡因子更新的第一种情况

2.2.2. 平衡因子更新的第二种情况

2.2.3. 平衡因子更新的第三种情况

2.2.4. 平衡因子更新的代码框架如下

2.2. AVL 树的旋转

2.2.1. 左单旋

2.2.2. 右单旋

2.2.3. 左右双旋

2.2.4. 右左双旋

2.3. 验证 AVL 树的插入

2.4. AVL 树插入的完整实现

1. AVL 树

1.1. AVL 树的概念

AVL树是一种自平衡的二叉搜索树，它以其发明者 G.M.Adelson-Velsky 和 E.M.Landis 的名字命名。AVL树保持树的左右子树高度的平衡，使得树的整体高度相对较小，提供了快速的查找、插入和删除操作。

在 AVL 树中，每个节点都包含一个键值对，且满足以下性质：

左子树中的所有节点的键都小于该节点的键；
右子树中的所有节点的键都大于该节点的键；
每个节点的左子树和右子树的高度差（平衡因子）最多为 1。

为了维持这种平衡，AVL树在每次插入或删除节点时会根据需要进行旋转操作。旋转操作包括左旋和右旋，并通过重新分配节点的位置使得AVL树重新平衡。这种自平衡的机制保证了AVL树的高度始终保持在较小的范围内，时间复杂度为O(log n)。

相对于其他平衡二叉搜索树（如红黑树），AVL树的平衡因子要求更为严格，不允许有任何节点的平衡因子绝对值超过1。这使得AVL树的修改操作更加频繁，但在查询操作上性能优于红黑树。

总结来说，AVL树是一种自平衡二叉搜索树，通过保持树的左右子树高度的平衡来提供快速的查找、插入和删除操作。它在每个节点上维护了平衡因子，并通过旋转操作来保持树的平衡性。这种自平衡的特性使得AVL树在一些对插入和删除操作要求较频繁的场景中具有优势。

1.2. AVL 树的性质

AVL树具有以下几个性质：

二叉搜索树：AVL树是一种二叉搜索树，需要满足以下性质：

左子树中的所有节点的键都小于该节点的键；

右子树中的所有节点的键都大于该节点的键；

左右子树都是二叉搜索树。

平衡性：AVL树的关键特点是保持平衡，即每个节点的左子树和右子树的高度差（平衡因子）最多为 1，确保了树的整体高度相对较小；
平衡因子：每个节点都有一个平衡因子，定义为右子树的高度减去左子树的高度（或左子树的高度减去右子树的高度）。平衡因子只能为 -1、0 或 1。
自平衡：当进行插入或删除操作导致AVL树不再平衡时，AVL树会通过旋转操作来恢复平衡。旋转操作包括左旋和右旋以及左右双旋和右左双旋，并通过重新分配节点的位置调整树的结构，使得树重新达到平衡状态；
高效性：由于AVL树的平衡性，其高度相对较小，从而保证了查找、插入和删除操作的平均时间复杂度为 O(log n)。

综上所述，AVL树是一种平衡二叉搜索树，具有二叉搜索树的性质，同时通过自平衡保持平衡性。它的平衡性和高效性使得它在某些场景中具有优势。

注意：AVL树不一定有平衡因子(balance factor)，我们在这里使用平衡因子只是它的一种实现方式，并且在这里我们的平衡因子 = 右子树的高度 - 左子树的高度。

2. AVL 树的框架如下

如下图所示：这就是一颗AVL树

我们在这里实现的 AVL 树采用三叉链的形式，大致框架如下：

namespace Xq
{template<class K,class V>struct avl_tree_node{// 采用三叉链的形式avl_tree_node<K,V>* _left;avl_tree_node<K,V>* _right;avl_tree_node<K,V>* _parent;std::pair<K,V> _kv;int _bf;  // balance factor 平衡因子avl_tree_node(const std::pair<K,V>& kv = std::pair<K,V>()):_left(nullptr),_right(nullptr),_parent(nullptr),_kv(kv),_bf(0)  {}};template<class K,class V>class avl_tree{private:typedef avl_tree_node<K,V> Node;public:avl_tree(Node* root = nullptr):_root(root){}bool insert(const std::pair<K,V>& kv){}private:private:Node* _root;};
}

2. AVL树的插入

AVL树的插入元素，也符合普通二叉搜索树的原则，找到合适的位置进行插入元素。

我们可以将AVL树的insert分为三个过程：

找到合适位置；
构造新节点，并完成连接关系；
更新平衡因子，如果平衡因子的绝对值 > 1，需要进行旋转处理。

2.1. 平衡因子的更新

平衡因子的更新：

如果平衡因子更新的整个过程，平衡因子没有出现问题 (平衡因子的绝对值 |bf|<= 1)，那么说明插入对AVL树的平衡结构不影响，不需要处理；
如果平衡因子更新的整个过程中，一旦平衡因子出现问题 (平衡因子的绝对值大于1)，平衡结构受到影响，需要停止更新，并进行旋转处理。

旋转分为四种：左旋、右旋、左右双旋、右左双旋。

插入新增节点，会影响祖先的 bf (全部或者部分祖先)。

平衡因子的更新有三种情况：

那么，什么决定了平衡因子是否要继续往上更新？取决于 parent 的所在的子树高度(即左右子树高度的较大值)是否变化？

如果变了 (例如会影响祖先的平衡因子(全部或部分)) 继续更新，不变则不再更新。

假设 cur 是新增节点，那么：

如果 cur == parent->right 那么父亲 parent 的平衡因子bf++；
如果 cur == parent->left 那么父亲 parent 的平衡因子bf--。

注意：插入之前我们需要保证原树是一颗AVL树，因此插入之前所有节点的|bf| <= 1。

2.2.1. 平衡因子更新的第一种情况

平衡因子更新后： parent->bf == 1 || parent->bf == -1；

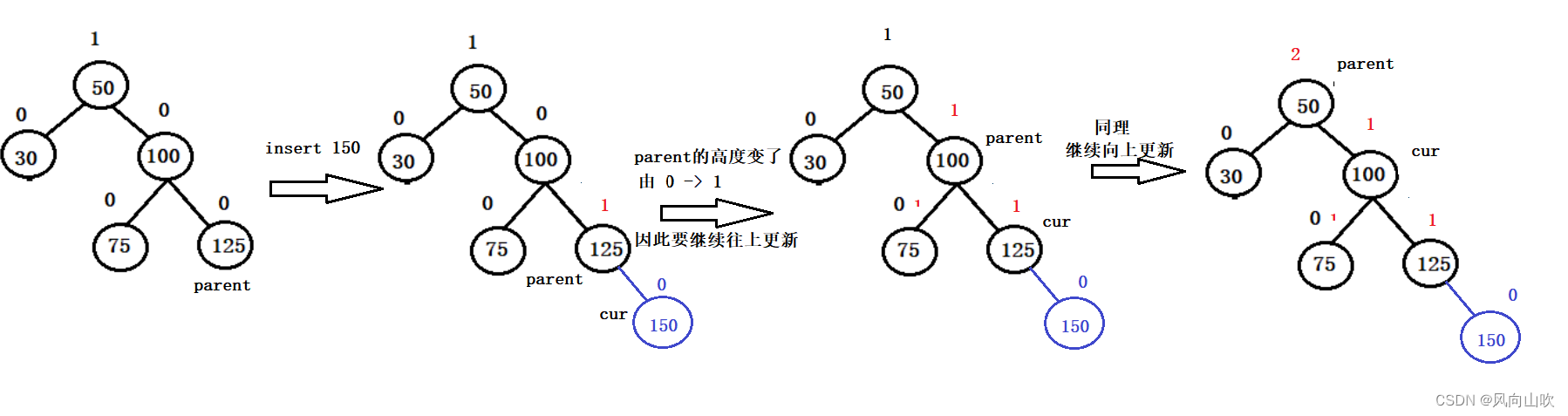
此时说明 parent 所在的子树的高度变了，继续向上更新，为什么？

因为插入元素之后 parent 的 bf==1 或者 bf ==-1，那么说明插入之前 parent->bf == 0，说明原左右子树的高度相等，现在有一边的子树高度高1，说明 parent 一边高一边低，高度变了，继续向上更新。

如图所示：

2.2.2. 平衡因子更新的第二种情况

平衡因子更新后：parent->bf == 0；

此时说明 parent 所在的子树高度不变，不用继续往上更新，这一次插入了就结束。

因为插入元素之后 parent 的 bf == 0，那么说明插入之前 parent->bf == 1 || parent->bf == -1，即插入之前一边高一边低，新增节点插入在矮的那边，插入之后，左右子树高度相同，parent 的高度不变，因此此时平衡因子不用向上更新了，插入结束。

如图所示：

2.2.3. 平衡因子更新的第三种情况

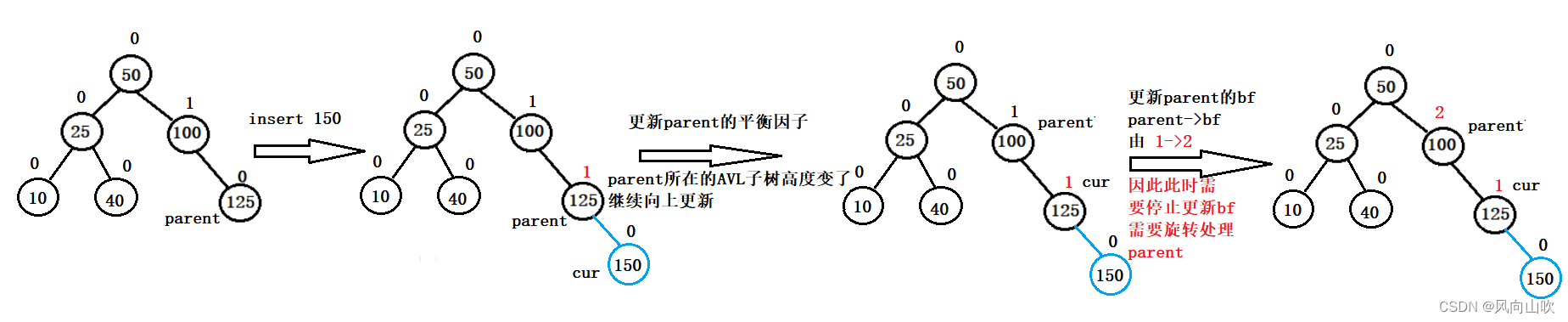
平衡因子更新后：parent->bf == -2 || parent->bf == 2

说明插入新增节点后 parent 的所在的子树不平衡（|bf| >= 2），因此需要停止向上更新，处理这颗子树，如何处理？旋转处理，处理完插入就结束。

如图所示：

2.2.4. 平衡因子更新的代码框架如下

while (parent)
{if (cur == parent->_left)--parent->_bf;else++parent->_bf;//case 1:  继续向上更新if (parent->_bf == 1 || parent->_bf == -1){cur = parent;parent = parent->_parent;continue;}// case 2: 符合AVL树,结束更新else if (parent->_bf == 0){break;}// case 3: 当前子树出现问题了(|bf| >= 2),需要停止更新,处理当前AVL子树,处理后,插入结束else if (parent->_bf == 2 || parent->_bf == -2){// 旋转处理:break;}// case 4:非法情况,说明前面的AVL树不符合规则else{// 直接断死assert(false);}
}

2.2. AVL 树的旋转

旋转操作是为了保持或恢复AVL树的平衡性。

AVL树的平衡在于每个节点的左子树和右子树的高度差（平衡因子）最多为 1。当进行插入或删除操作后，可能会打破原本的平衡性，导致某个节点的平衡因子超过了允许的范围。

为了恢复平衡，AVL树采用不同类型的旋转操作，包括左旋和右旋。旋转操作通过重新分配节点的位置，使得树重新达到平衡状态，确保每个节点的平衡因子保持在允许的范围内。

旋转操作的具体目的如下：

1. 左旋：当一个节点的右子树高度大于左子树高度时 (高度相差 >= 2)，进行左旋操作。左旋将当前节点和其右子节点进行交换，使得原先的右子节点成为新的根节点，同时保证原来左子树不变、右子节点的左子树作为新的右子树，从而降低了树的高度差；
2. 右旋：当一个节点的左子树高度大于右子树高度时 (高度相差 >= 2)，进行右旋操作。右旋将当前节点和其左子节点进行交换，使得原先的左子节点成为新的根节点，同时保证原来右子树不变、左子节点的右子树作为新的左子树，从而降低了树的高度差。

通过旋转操作，AVL树可以在插入或删除节点后自动调整自己，降低AVL树的高度，维持其平衡结构 ，提供更高效的查找、插入和删除操作。

总结来说，旋转操作的目的是为了保持或恢复AVL树的平衡性，通过重新分配节点的位置降低树的高度差，确保每个节点的平衡因子在允许范围内。这样可以提供更好的性能和效率。

旋转处理的情况分为四种：左单旋、右单旋、左右双旋、右左双旋；
旋转的原则：旋转后仍是一颗AVL树；
旋转的目的：左右均衡，降低整棵AVL树的高度。

我们依次来看：

2.2.1. 左单旋

如下图所示：

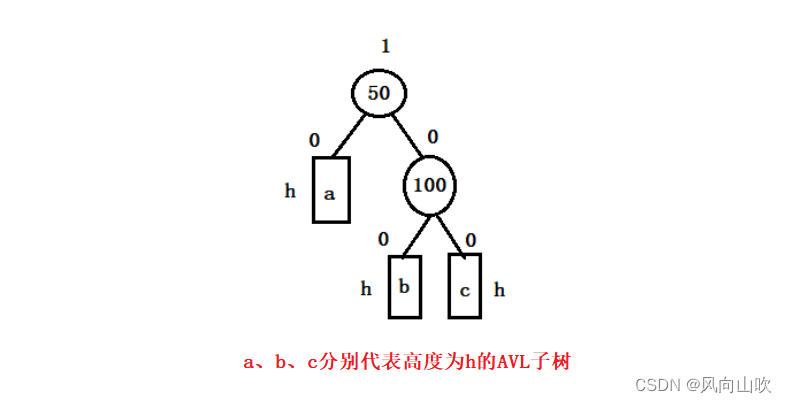
当h==0时，情况如下：

当h==1时，情况如下：

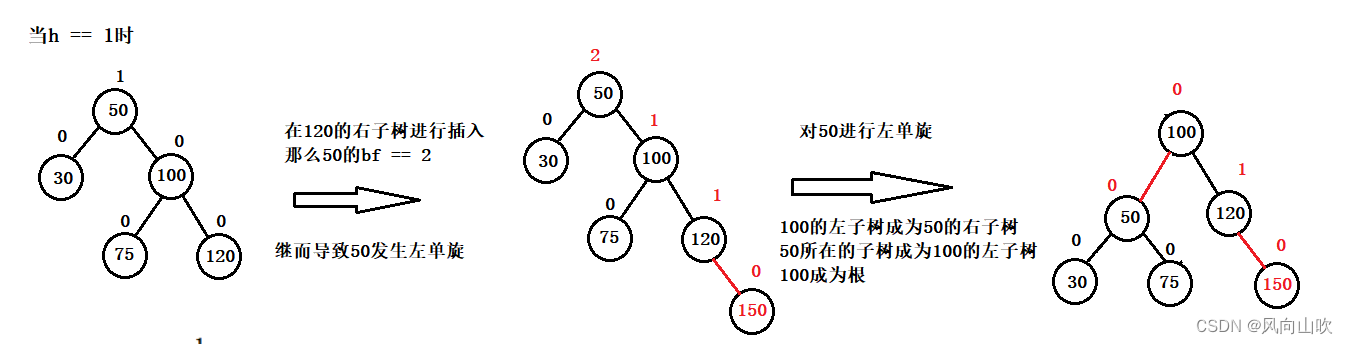
当h == 2时，情况如下：

上面列出了三种情况，当然远远不止，虽然有很多种情况，但是对于AVL树的左单旋的处理方式是固定的：

只要满足 cur->bf == 2 && cur_right->bf == 1，那么就对cur进行左单旋。

旋转后将 cur 和 cur_right 的平衡因子置为0即可。

具体如下图所示：

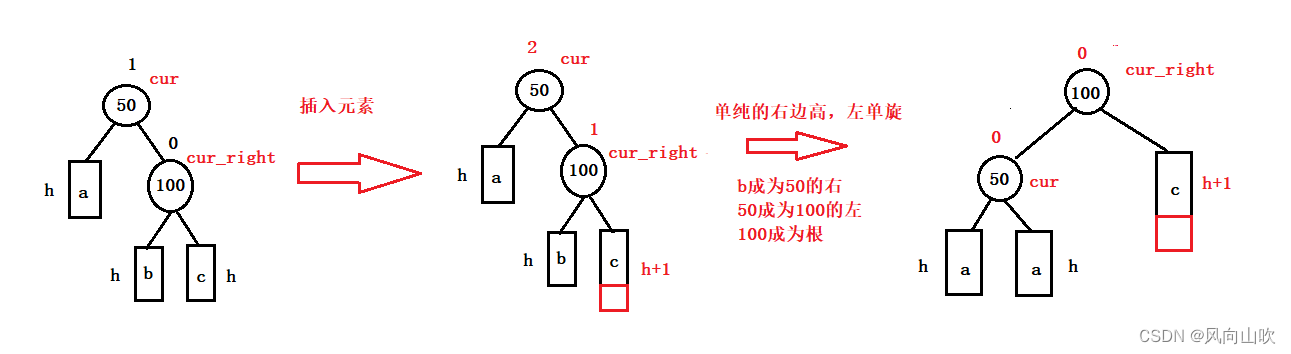
有了上面的分析，我们可以得出结论：

当cur->bf == 2 && cur_right->bf == 1，那么就对cur进行左单旋

旋转后更新平衡因子：cur->bf = 0; cur_right->bf = 0;

因此，我们的左单旋实现如下：

为了更好地实现左单旋，我们借助下面的图来实现

实现代码如下：

void left_rotate(Node* parent)
{// 确立四个节点的初始位置Node* cur = parent;Node* cur_right = cur->_right;Node* cur_right_left = cur_right->_left;Node* cur_parent = cur->_parent;cur->_right = cur_right_left;// 当h == 0时,cur_right_left是为空的,因此在这里要判断一下if (cur_right_left)cur_right_left->_parent = cur;cur_right->_left = cur;cur->_parent = cur_right;// 如果parent是根节点,那么cur_right就是新根if (!cur_parent){cur_right->_parent = nullptr;_root = cur_right;}// 如果parent不是根节点,那么cur_parent不为空else{if (cur_parent->_kv.first > cur_right->_kv.first){cur_parent->_left = cur_right;}else{cur_parent->_right = cur_right;}cur_right->_parent = cur_parent;}// 更新cur和cur_right的平衡因子cur_right->_bf = cur->_bf = 0;
}

2.2.2. 右单旋

对于右单旋来说，分析思路与左单旋差别不大，只不过右单旋是单纯的左边高，进行右单旋，在这里只以 h==1 的具象图和抽象图用以举例说明：

当h==1时，如下图所示：

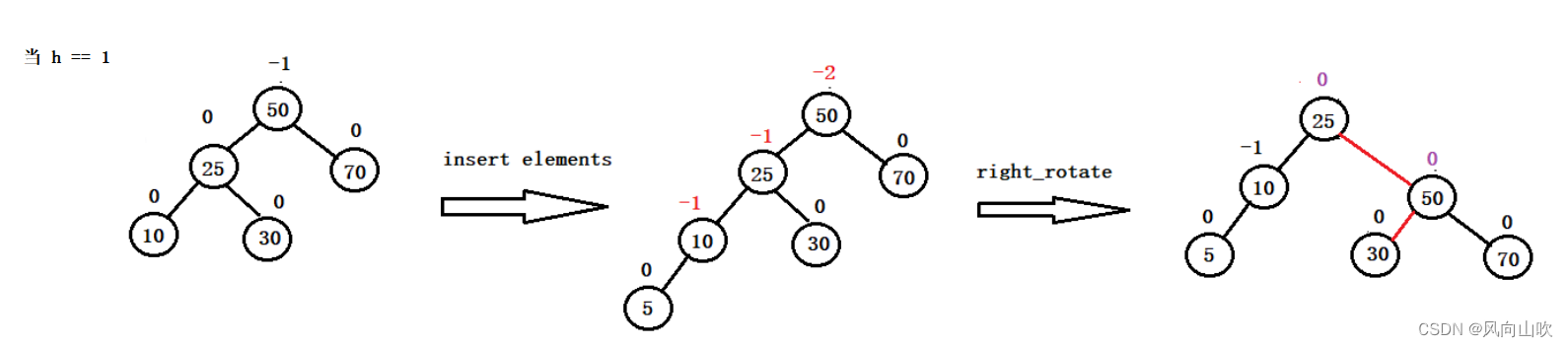
右单旋的抽象图，如下图所示：

与左单旋同样，虽然右单旋会有很多种情况，但是它们的处理方式是一样的，只要满足

cur->bf == -2 && cur_left->bf == -1 就对cur进行右单旋，旋转玩后将 cur 和 cur_left 的 bf 更新为0，旋转结束。

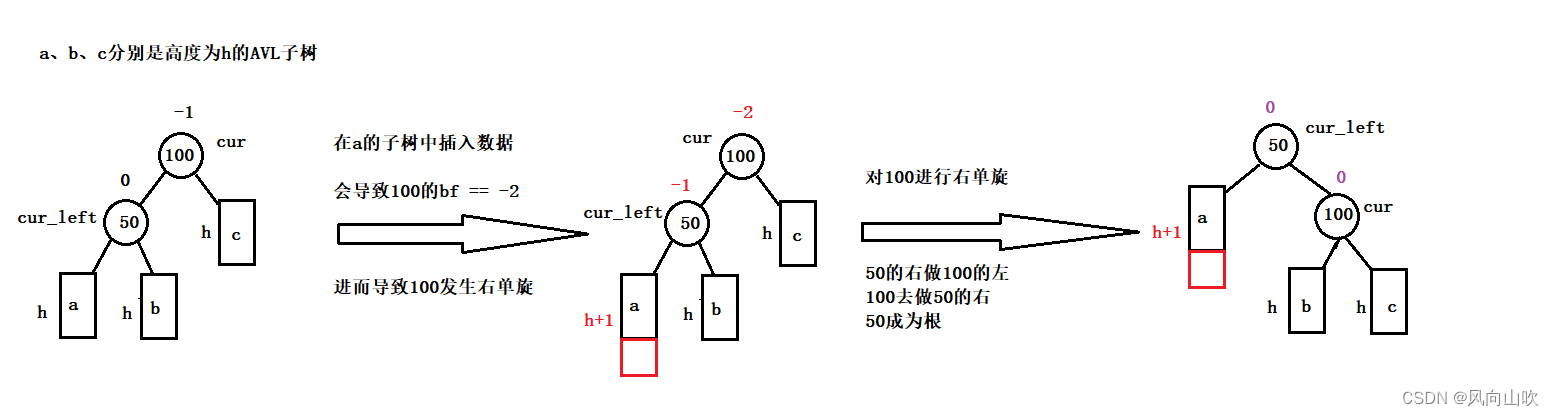
有了上面的分析，我们可以得出结论：

当cur->bf == -2 && cur_left->bf == -1，那么就对cur进行右单旋

旋转后更新平衡因子cur->bf = 0; cur_left->bf = 0;

因此，我们的右单旋实现如下：

为了更好地实现右单旋，我们借助下面的图来实现：

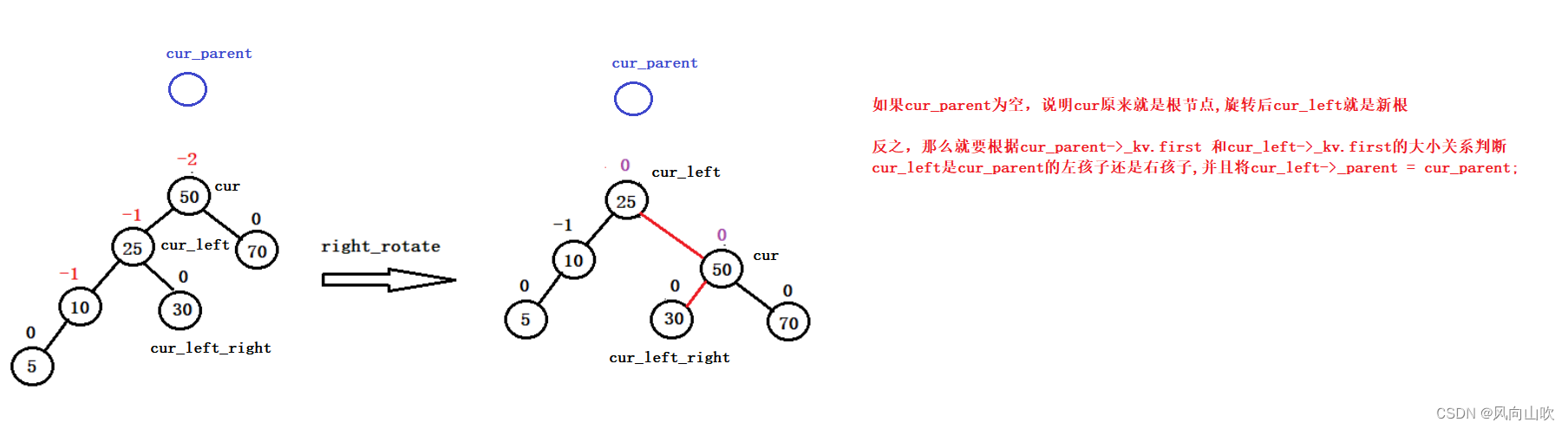
右单旋实现代码如下：

void right_rotate(Node* parent)
{// 确立四个节点的初始位置Node* cur = parent;Node* cur_left = cur->_left;Node* cur_left_right = cur_left->_right;Node* cur_parent = cur->_parent;cur->_left = cur_left_right;// 当h == 0时,cur_left_right为空,因此在这里要判断一下if (cur_left_right)cur_left_right->_parent = cur;cur_left->_right = cur;cur->_parent = cur_left;// 如果cur_parent为空,那么cur_left就是新根if (!cur_parent){cur_left->_parent = nullptr;_root = cur_left;}else{// 在这里需要判断一下kv.first的大小，以确定cur_left是左孩子还是右孩子if (cur_parent->_kv.first > cur_left->_kv.first){cur_parent->_left = cur_left;}else{cur_parent->_right = cur_left;}// 最后也要链接父亲cur_left->_parent = cur_parent;}// 更新平衡因子cur->_bf = cur_left->_bf = 0;
}

2.2.3. 左右双旋

左右双旋：‘例如这种形状<’，整体看是左边高，但是左子树又是右边高。

此时需要：先对左子树进行左单旋、在对整体进行右单旋。

先左单旋的目的是：让这棵AVL子树变成单纯的左边高，在进行右单旋。

如图所示：

当h == 0时，如下图所示

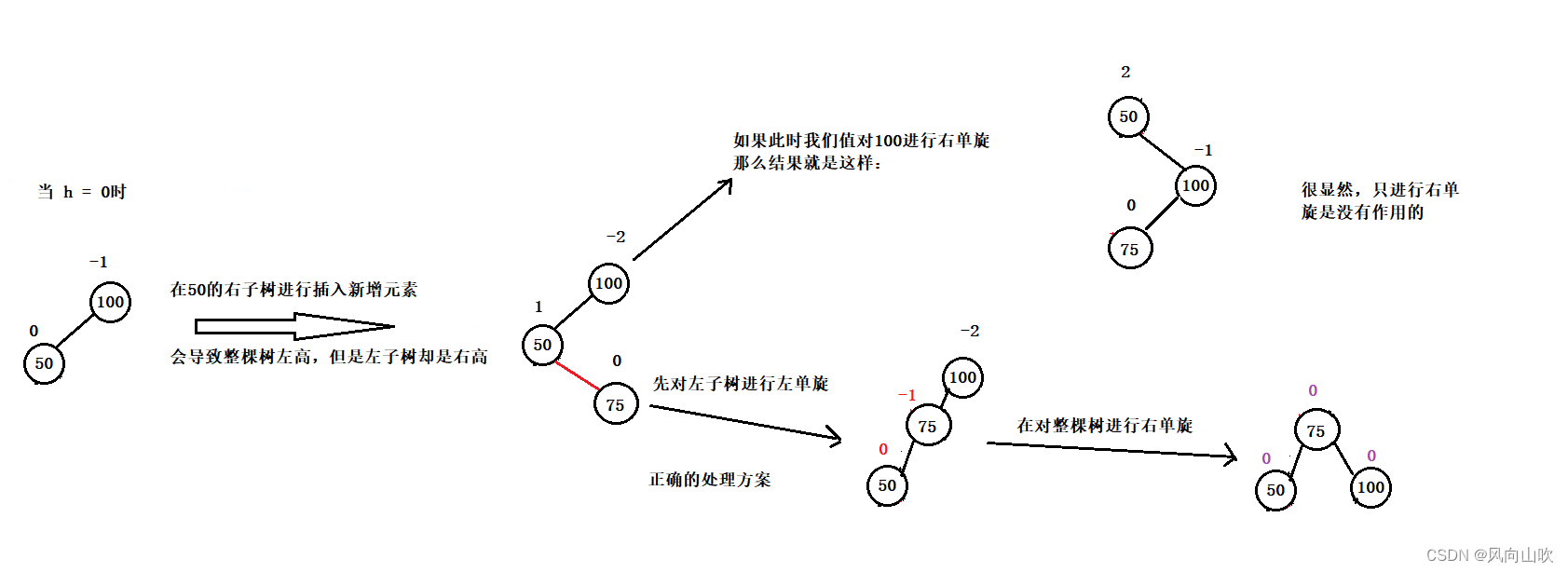
当 h == 1时，如下图说式：

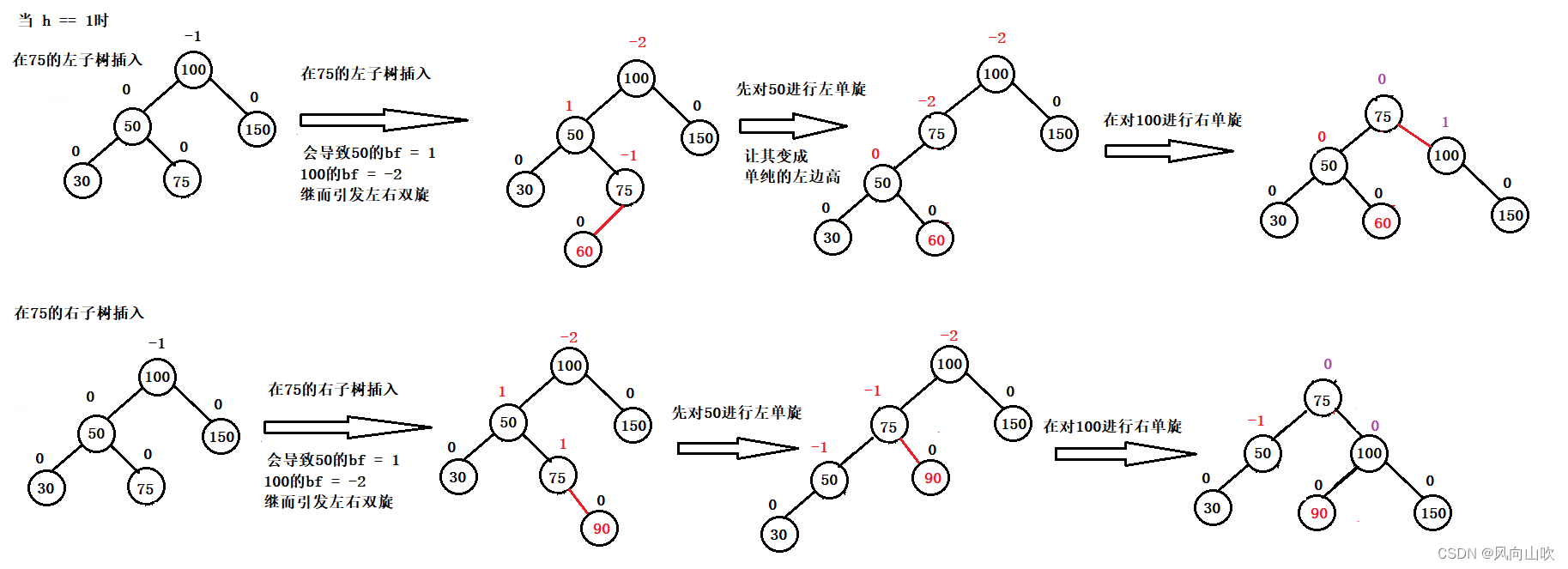
左右双旋的抽象图：

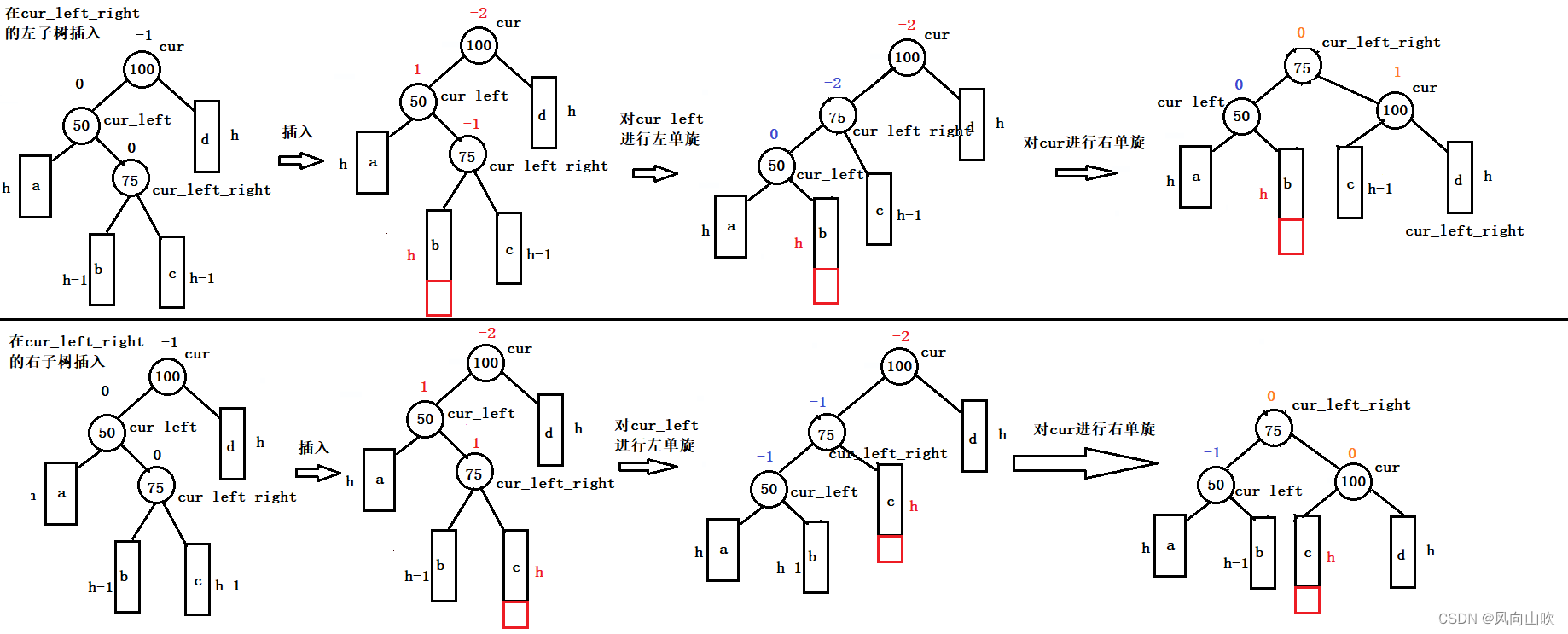
将上面的图联系到一起，我们可以发现，它们的旋转方式和旋转条件是一样的。

旋转条件： cur->bf == -2 && cur_left->bf == 1 (对应到上图：(100就是cur, 50就是cur_left) )

旋转方式：先对左子树进行左单旋，在对整体进行右单旋。

但是最后的平衡因子的更新却不一样，可以分为三种情况

当插入元素后：

case 1：cur_left_right->bf == 0
旋转后：cur->bf = 0; cur_left->bf = 0; cur_left_right->_bf = 0;
case 2：cur_left_right->bf == -1
旋转后：cur->bf = 1; cur_left->bf = 0; cur_left_right->_bf = 0;
case 3：cur_left_right->bf == 1
旋转后：cur->bf = 0; cur_left->bf = -1; cur_left_right->_bf = 0;

左右双旋的代码如下：

void left_right_rotate(Node* parent)
{Node* cur = parent;Node* cur_left = cur->_left;Node* cur_left_right = cur_left->_right;int bf = cur_left_right->_bf;// 先左旋、后右旋left_rotate(cur_left);right_rotate(cur);if (bf == 0){cur->_bf = 0;cur_left->_bf = 0;cur_left_right->_bf = 0;}else if (bf == -1){cur->_bf = 1;cur_left->_bf = 0;cur_left_right->_bf = 0;}else if (bf == 1){cur->_bf = 0;cur_left->_bf = -1;cur_left_right->_bf = 0;}else{// 非法情况,直接断死assert(false);}
}

2.2.4. 右左双旋

右左双旋的分析思路和左右双旋没有太大差异。在这里只以h == 0 和对应的抽象图举例分析其中细节。

如图所示，这就是右左双旋的抽象图：

当h == 0时的具象图，如下图所示：

剩下两种情况的抽象图，如下图所示：

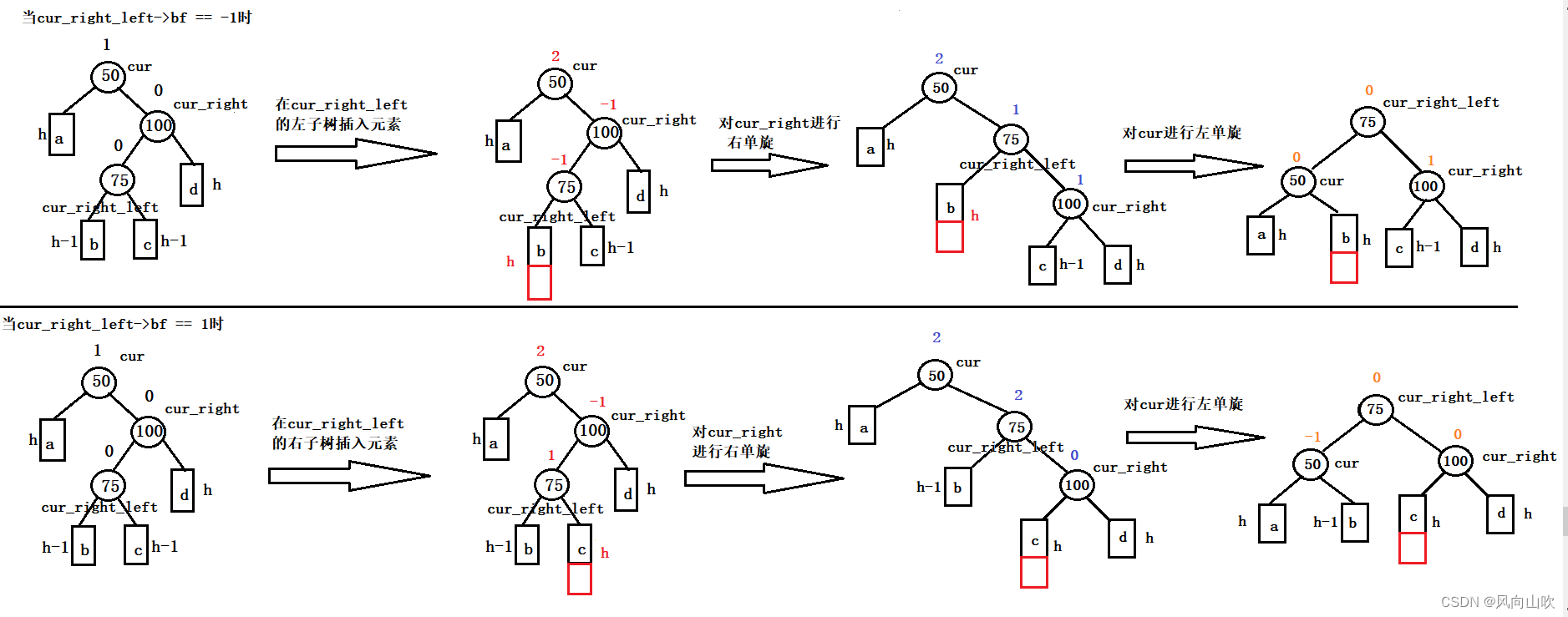
将上面的图联系到一起，我们可以发现，他们的旋转方式和旋转条件是一样的。

旋转条件: cur->bf == 2 && cur_right->bf == -1 (对应到上图:(50就是cur,100就是cur_right))

旋转方式：先对右子树进行右单旋，在对整体进行左单旋。

但是最后的平衡因子的更新却不一样，可以分为三种情况

当插入元素后：

case 1：cur_right_left->bf == 0
旋转后：cur->bf = 0;cur_right->bf = 0; cur_right_left->bf = 0;
case 2：cur_right_left->bf == -1
旋转后：cur->bf = 0;cur_right->bf = 1; cur_right_left->bf = 0;
case 3：cur_right_left->bf == 1
旋转后：cur->bf = -1;cur_right->bf = 0; cur_right_left->bf = 0;

右左双旋代码如下：

void right_left_rotate(Node* parent)
{Node* cur = parent;Node* cur_right = cur->_right;Node* cur_right_left = cur_right->_left;int bf = cur_right_left->_bf;right_rotate(cur_right);left_rotate(cur);if (bf == 0){cur->_bf = 0;cur_right->_bf = 0;cur_right_left->_bf = 0;}else if (bf == -1){cur->_bf = 0;cur_right->_bf = 1;cur_right_left->_bf = 0;}else if (bf == 1){cur->_bf = -1;cur_right->_bf = 0;cur_right_left->_bf = 0;}else{// 非法情况,直接断死assert(false);}
}

2.3. 验证 AVL 树的插入

如何验证：

我们需要验证每一棵 AVL 子树的左右子树高度差是否小于等于1，且要判断每个节点的平衡因子是否等于当前节点的左右子树的高度差。

代码实现：

// 得到子树的高度
int _get_tree_high(Node* root)
{if (!root)return 0;else{int left_high = _get_tree_high(root->_left);int right_high = _get_tree_high(root->_right);return left_high > right_high ? ++left_high : ++right_high;}
}bool _is_balance_tree(Node* root)
{// 空树可以认为是AVL树if (!root)return true;else{// 左子树的高度int left_high = get_tree_high(root->_left);// 右子树的高度int right_high = get_tree_high(root->_right);// 如果当前节点的平衡因子不等于当前节点的左右子树的高度差,说明异常if (right_high - left_high != root->_bf){std::cout << root->_kv.first << " : 该节点的平衡因子出现异常" << std::endl;return false;}// 计算每颗AVL子树的左右子树高度差,如果存在大于1的情况,说明异常int bf = right_high - left_high;if (bf < 0)bf *= -1;return bf <= 1&& _is_balance_tree(root->_left)&& _is_balance_tree(root->_right);}
}

2.4. AVL 树插入的完整实现

#pragma once
#include <iostream>
#include <assert.h>
#include <queue>
#include <vector>
#include <utility>
#include <time.h>namespace Xq
{template<class K,class V>struct avl_tree_node{avl_tree_node<K,V>* _left;avl_tree_node<K,V>* _right;avl_tree_node<K,V>* _parent;std::pair<K,V> _kv;int _bf;  // balance factoravl_tree_node(const std::pair<K,V>& kv = std::pair<K,V>()):_left(nullptr),_right(nullptr),_parent(nullptr),_kv(kv),_bf(0){}};template<class K,class V>class avl_tree{private:typedef avl_tree_node<K,V> Node;public:avl_tree(Node* root = nullptr):_root(root){}bool insert(const std::pair<K,V>& kv){if(_root == nullptr){_root = new Node(kv);return true;}else{Node* cur = _root;Node* parent = nullptr;while(cur){if(cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else if(cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else{return false;}}cur = new Node(kv);if(kv.first > parent->_kv.first){parent->_right = cur;cur->_parent = parent;}else{parent->_left = cur;cur->_parent = parent;}// 调整平衡因子while(parent){if(cur == parent->_left)--parent->_bf;else++parent->_bf;//case 1:  继续向上更新if(parent->_bf == 1 || parent->_bf == -1){cur = parent;parent = parent->_parent;continue;}// case 2: 符合AVL树,结束更新else if(parent->_bf == 0){break;}// case 3: 当前子树出现问题了(|bf| >= 2),需要停止更新,处理当前AVL子树,处理后,插入结束else if(parent->_bf == 2 || parent->_bf == -2){// 旋转处理://case 1: 左单旋if(parent->_bf == 2 && parent->_right->_bf == 1){left_rotate(parent);}//case 2: 右单旋else if(parent->_bf == -2 && parent->_left->_bf == -1){right_rotate(parent);}//case 3:左右双旋else if(parent->_bf == -2 && parent->_left->_bf == 1){left_right_rotate(parent);}//case 4:右左双旋else if(parent->_bf == 2 && parent->_right->_bf == -1){right_left_rotate(parent);}//非法情况,断死else {assert(false);}break;}// case 4:非法情况,说明前面的AVL树不符合规则else{// 直接断死assert(false);}}return true;}}void left_rotate(Node* parent){// 1. 确立四个节点的初始位置Node* cur = parent;Node* cur_right = cur->_right;Node* cur_right_left = cur_right->_left;Node* cur_parent = cur->_parent;cur->_right = cur_right_left;// 当h == 0时,cur_right_left是为空的,因此在这里要判断一下if(cur_right_left)cur_right_left->_parent = cur;cur_right->_left = cur;cur->_parent = cur_right;// 如果parent是根节点,那么cur_right就是新根if(!cur_parent){cur_right->_parent = nullptr;_root = cur_right;}// 如果parent不是根节点,那么cur_parent不为空else{if(cur_parent->_kv.first > cur_right->_kv.first){cur_parent->_left = cur_right;}else{cur_parent->_right = cur_right;}cur_right->_parent = cur_parent;}cur->_bf = cur_right->_bf = 0;}void right_rotate(Node* parent){// 确立四个节点的初始位置Node* cur = parent;Node* cur_left = cur->_left;Node* cur_left_right = cur_left->_right;Node* cur_parent = cur->_parent;cur->_left = cur_left_right;// 当h == 0时,cur_left_right为空,因此在这里要判断一下if(cur_left_right)cur_left_right->_parent = cur;cur_left->_right = cur;cur->_parent = cur_left;// 如果cur_parent为空,那么cur_left就是新根if(!cur_parent){cur_left->_parent = nullptr;_root = cur_left;}else{if(cur_parent->_left == cur){cur_parent->_left = cur_left;}else{cur_parent->_right = cur_left;}cur_left->_parent = cur_parent;}// 更新平衡因子cur->_bf = cur_left->_bf = 0;}void left_right_rotate(Node* parent){Node* cur = parent;Node* cur_left = cur->_left;Node* cur_left_right = cur_left->_right;int bf = cur_left_right->_bf;// 先左旋、后右旋left_rotate(cur_left);right_rotate(cur);if(bf == 0){cur->_bf = 0;cur_left->_bf = 0;cur_left_right->_bf = 0;}else if(bf == -1){cur->_bf = 1;cur_left->_bf = 0;cur_left_right->_bf = 0;}else if(bf == 1){cur->_bf = 0;cur_left->_bf = -1;cur_left_right->_bf = 0;}else {// 非法情况,直接断死assert(false);}}void right_left_rotate(Node* parent){Node* cur = parent;Node* cur_right = cur->_right;Node* cur_right_left = cur_right->_left;int bf = cur_right_left->_bf;right_rotate(cur_right);left_rotate(cur);if(bf == 0){cur->_bf = 0;cur_right->_bf = 0;cur_right_left->_bf = 0;}else if(bf == -1){cur->_bf = 0;cur_right->_bf = 1;cur_right_left->_bf = 0;}else if(bf == 1){cur->_bf = -1;cur_right->_bf = 0;cur_right_left->_bf = 0;}else {// 非法情况,直接断死assert(false);}}void level_order(){_level_order(_root);}int get_tree_high(Node* root){return _get_tree_high(root);}bool is_balance_tree(){return _is_balance_tree(_root);}int in_outside_get_tree_high(){return _get_tree_high(_root);}private:void _level_order(Node* root){if(!root)return ;else{std::queue<Node*> qu;qu.push(root);while(!qu.empty()){Node* front = qu.front();qu.pop();if(front){qu.push(front->_left);qu.push(front->_right);}if(!front)std::cout << "N ";elsestd::cout << front->_kv.first << " ";}std::cout << std::endl;}}int _get_tree_high(Node* root){if(!root)return 0;else{int left_high = _get_tree_high(root->_left);int right_high = _get_tree_high(root->_right);return left_high > right_high ? ++left_high : ++right_high;}}bool _is_balance_tree(Node* root){// 空树可以认为是AVL树if(!root)return true;else{int left_high = get_tree_high(root->_left);int right_high = get_tree_high(root->_right);if(right_high - left_high != root->_bf){std::cout << root->_kv.first <<" : 该节点的平衡因子出现异常" << std::endl;return false;}// 计算每颗AVL子树的左右子树高度差,如果存在大于1的情况,说明异常int bf = right_high-left_high;if(bf < 0)bf *= -1;return bf <= 1 && _is_balance_tree(root->_left)&& _is_balance_tree(root->_right);}}private:Node* _root;};
}