NO.1

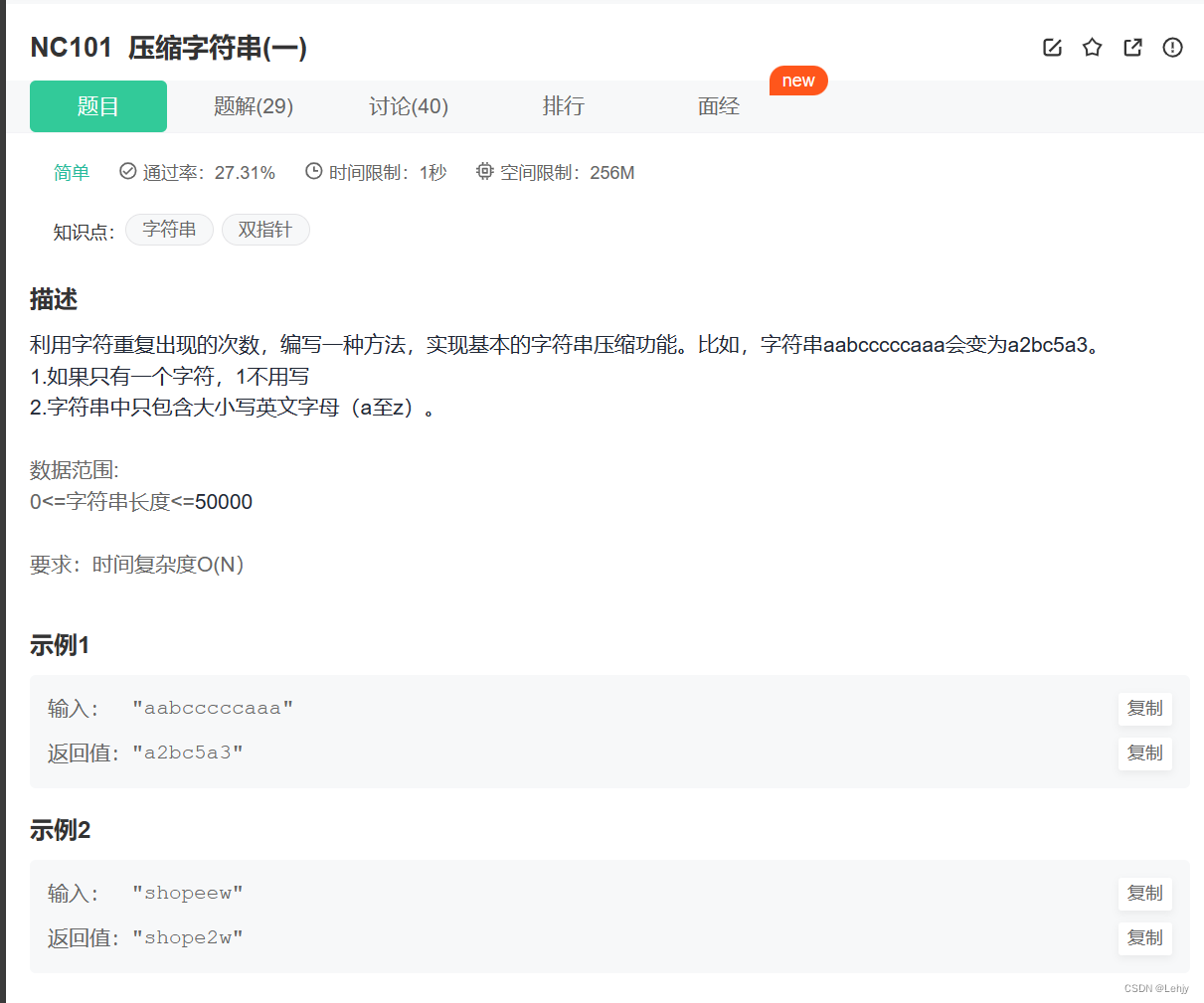
思路：双指针模拟。to_string将数字转化为字符。

代码实现：

class Solution {
public:string compressString(string param) {int left=0,right=0,n=param.size();string ret;while(right<n){while(right+1<n&&param[right]==param[right+1]) right++;int len=right-left+1;ret+=param[left];if(len>1){ret+=to_string(len);}left=right+1;right=left;}return ret;}
};

NO.2

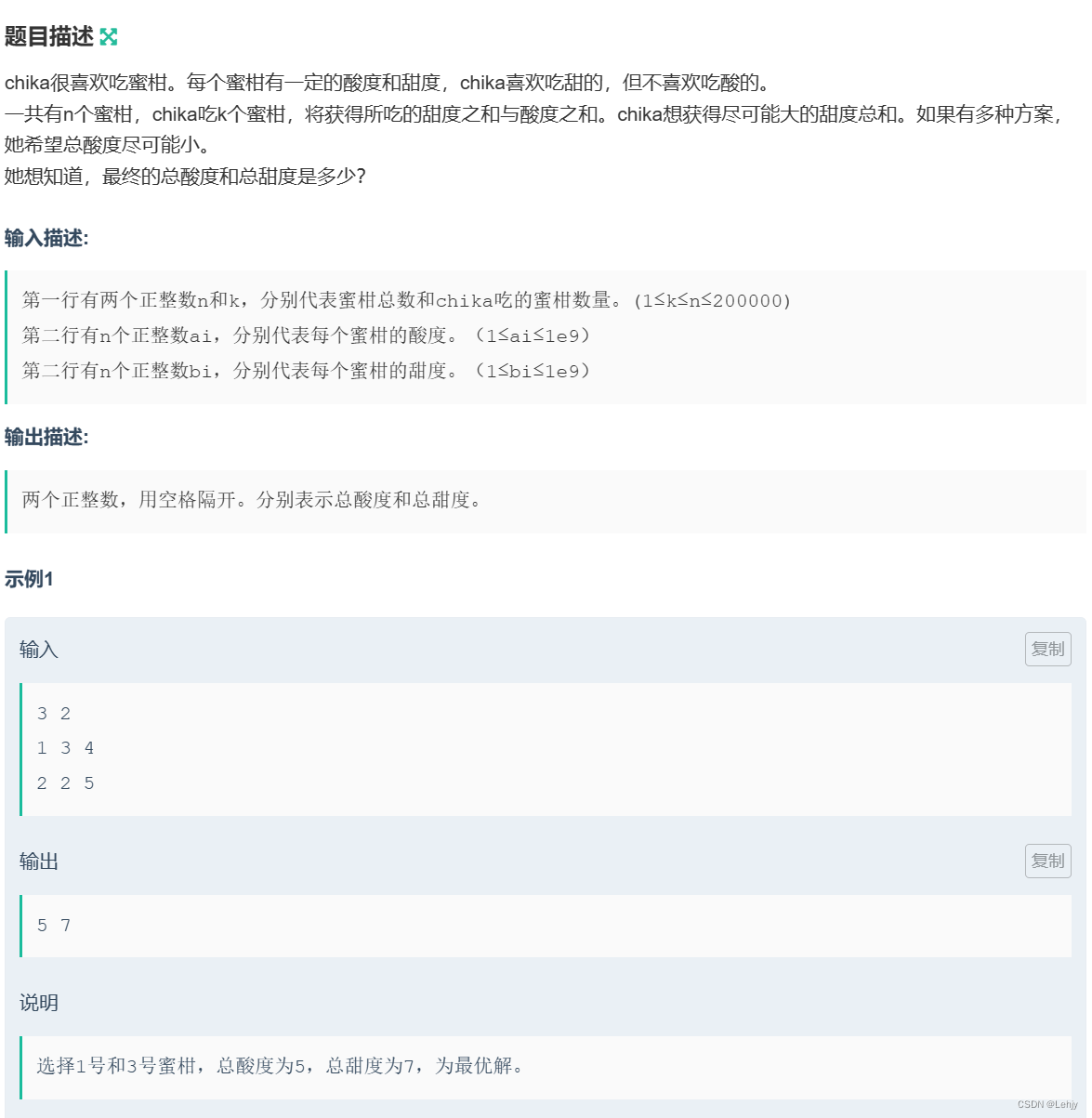
思路：建立一个pair数组，第一个位置存放酸度，第二个位置存放甜度，再给数组进行排序，实现甜度大优先，如果甜度相同就选择酸度小的，最后将k个数据的甜度和酸度的总和输出就可以了。

代码实现：

#include<iostream>
#include<algorithm>using namespace std;const int N=2e5+10;
typedef pair<int,int> PII;
int n,k;
PII arr[N];int main()
{cin>>n>>k;for(int i=0;i<n;i++) cin>>arr[i].first;for(int i=0;i<n;i++) cin>>arr[i].second;sort(arr,arr+n,[&](const PII& a,const PII& b){if(a.second!=b.second) return a.second>b.second;else return a.first<b.first;});long long s=0,t=0;for(int i=0;i<k;i++){s+=arr[i].first;t+=arr[i].second;}cout<<s<<" "<<t<<endl;return 0;
}

NO.3

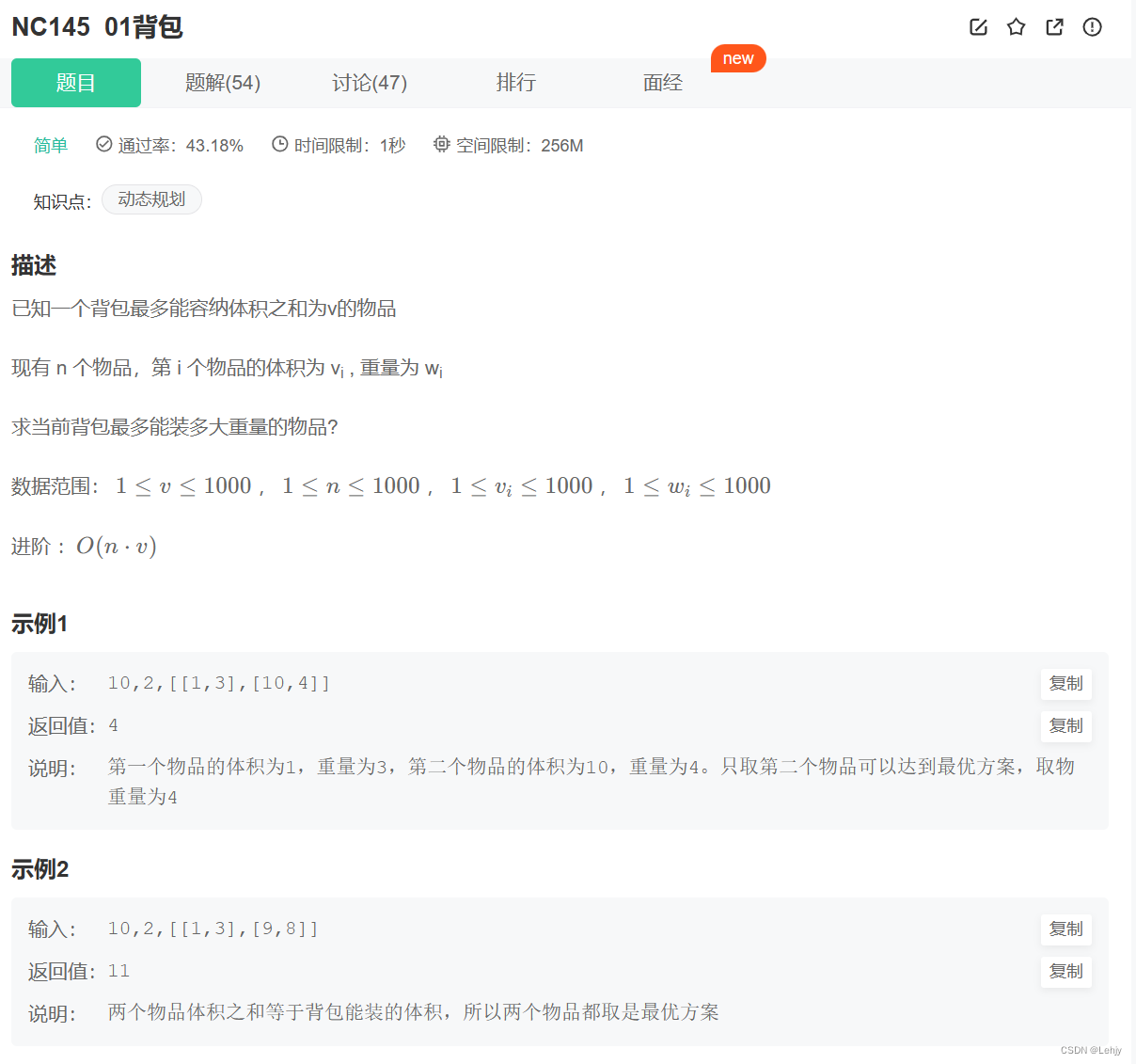
思路：

1. 状态表⽰：
   dp[i][j] 表⽰从前 i 个物品中挑选，总体积不超过 j 的情况下，最⼤重量是多少。
2. 状态转移⽅程：
   根据「最后⼀步」的状况，来分情况讨论：
   i. 不选第 i 个物品：相当于就是去前 i - 1 个物品中挑选，并且总体积不超过 j 。此时 dp[i][j] = dp[i - 1][j] ；
   ii. 选择第 i 个物品：那么我就只能去前 i - 1 个物品中，挑选总体积不超过 j - v[i]
   的物品。此时 dp[i][j] = dp[i - 1][j - v[i]] + w[i] 。但是这种状态不⼀定存在，因此需要特判⼀下。
   综上，状态转移⽅程为： dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - v[i]] + w[i]) 。
   3.实现空间优化，二位变成一维。

代码实现：

class Solution {
public:int dp[1010]={0};int knapsack(int V, int n, vector<vector<int> >& vw) {for(int i=0;i<n;i++){for(int j=V;j>=vw[i][0];j--){dp[j]=max(dp[j],dp[j - vw[i][0]] + vw[i][1]);}}return dp[V];}
};