Transformer - Self-Attention层的复杂度的计算

flyfish

矩阵的维度

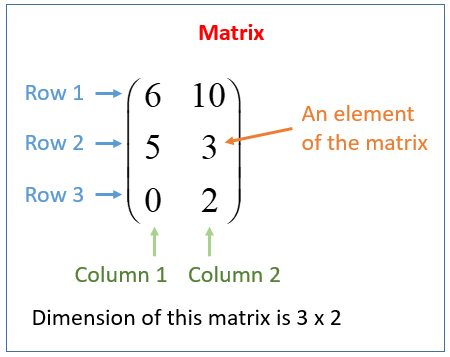
下面矩阵的维度是3×2即 3行，2列
6,10等都是矩阵里的元素

如果矩阵A的列数与矩阵B的行数相同，那么这两个矩阵可以相乘。即，若A是一个m×n矩阵，B是一个n×p矩阵，则它们的乘积C会是一个m×p矩阵。
中间相等，留两边。

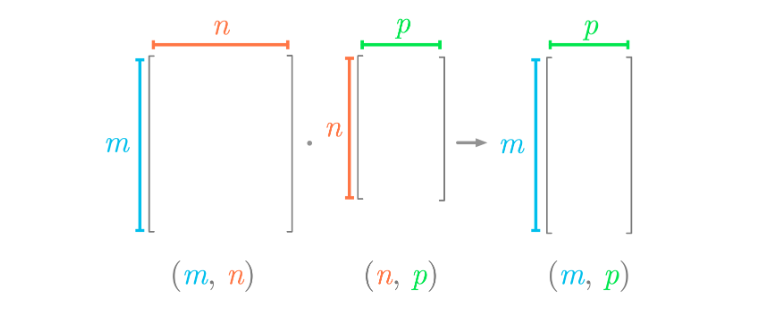
两个矩阵相乘的复杂度是 O(m×p×n)

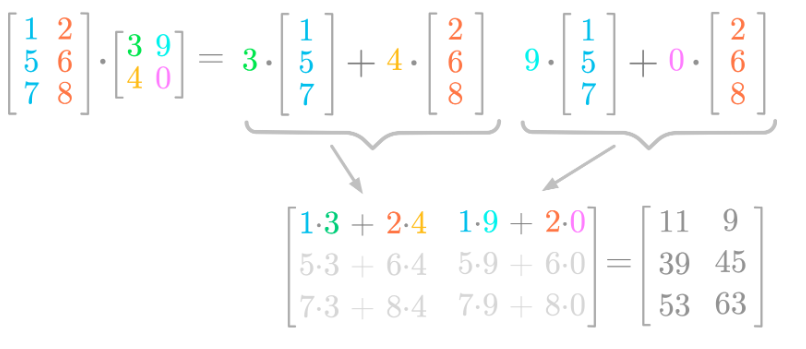
1. 乘法操作的数量：
   对于C中的每个元素c[i][j]，需要计算A的第i行与B的第j列对应元素的乘积之和，即求和m次乘法。因为C是一个m×p的矩阵，所以总共有m×p个这样的元素，因此总共需要做m×p×n次乘法操作。

2. 加法操作的数量：在计算每个c[i][j]时，除了乘法外，还需要进行n-1次加法操作（首次乘积直接赋值，之后每次乘积与累加和相加）。因此，总的加法操作次数也是m×p×(n-1)。

基本矩阵乘法的总操作数是乘法和加法操作次数之和，即大约2mpn次操作。因此，其时间复杂度为O(mpn)。

乘法通常是计算密集型操作中更耗时的部分，所以在大O表示法中通常关注乘法的次数。不过，确实也进行了相似数量级的加法操作，但这不影响大O表示法的阶数。

C是一个m×p的矩阵，它包含mp个元素。因此，总的乘法操作次数是mp乘以n，即m×p×n次

Self-Attention层的复杂度的计算

n 是序列的长度，d 是向量的长度
Query = n ×d
Key = d × n

复杂度的计算之前的字母是 O(m×p×n) ，现在是(n × n × d)，所以就是n的平方乘以d