异常检测 | PCA马氏距离异常值检测（Matlab）

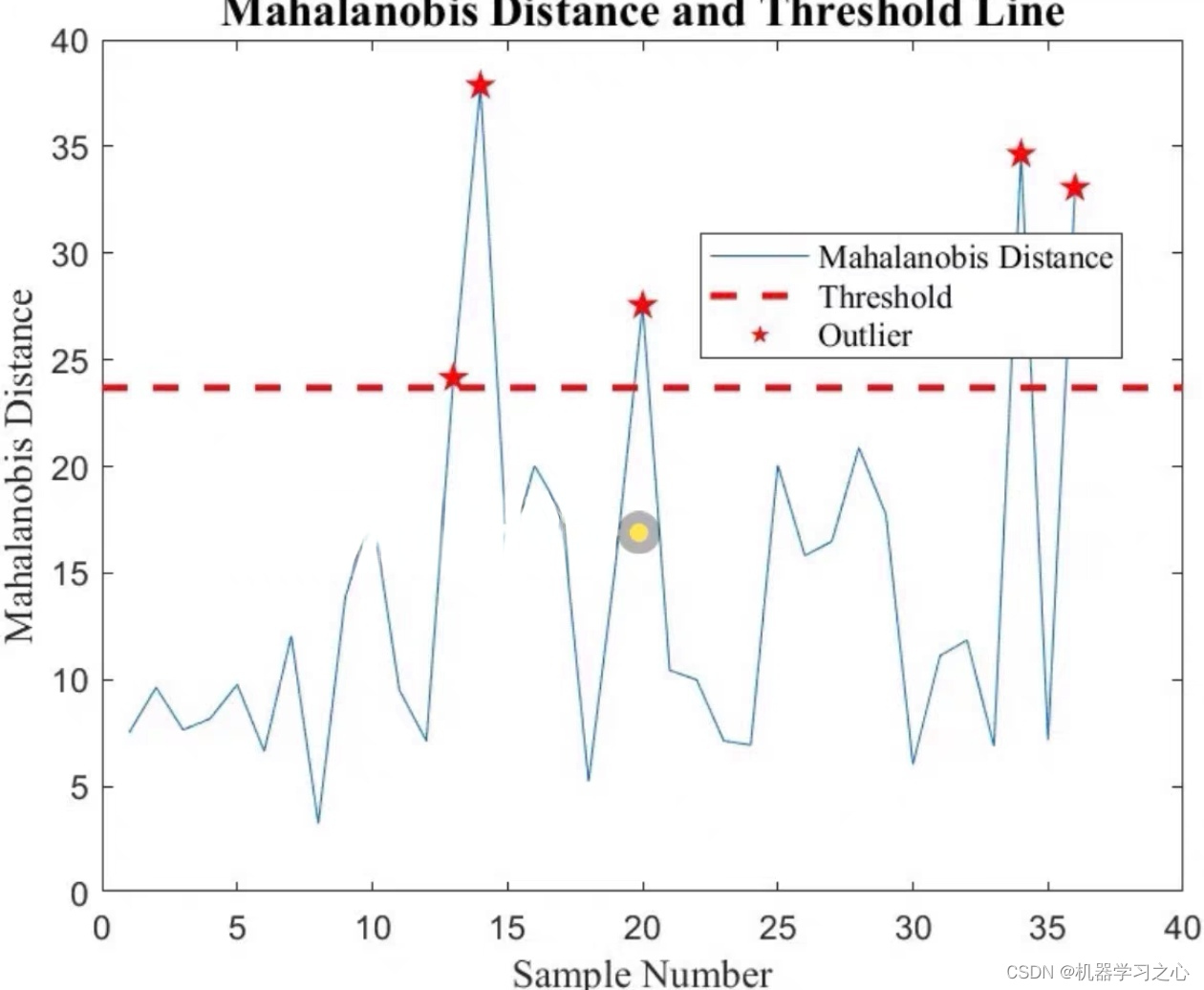
效果一览

基本介绍

Matlab Pca 马氏距离异常值检测，剔除异常样本，置信椭圆可选。
马氏距离异常值检测是一种常用的统计方法，用于识别数据集中的异常样本。它基于马氏距离的概念，计算每个样本点与数据集的均值之间的马氏距离，并将距离较大的样本点判定为异常。
一般步骤：
收集数据集：收集需要进行异常值检测的数据集。
计算均值和协方差矩阵：对于数据集中的所有特征，计算其均值和协方差矩阵。均值表示数据集的中心位置，协方差矩阵描述了数据集中各特征之间的关联性。
计算马氏距离：对于每个样本点，计算其与数据集均值之间的马氏距离。马氏距离可以通过以下公式计算： 马氏距离 = sqrt((x - μ)’ * Σ^(-1) * (x - μ)) 其中，x是样本点的特征向量，μ是数据集的均值向量，Σ是数据集的协方差矩阵。
设置阈值：根据需要，选择一个合适的阈值来判定哪些样本点被认为是异常。距离大于阈值的样本点被标记为异常值。
剔除异常样本：根据阈值，将被判定为异常的样本点从数据集中剔除。
关于置信椭圆作为可选项，它是一种可视化手段，用于表示数据的分布情况和异常点的位置。置信椭圆是根据数据集的均值和协方差矩阵绘制的椭圆，通常选择包含特定置信水平的椭圆，例如95%置信水平。通过观察数据点是否位于置信椭圆之外，可以初步判断其是否为异常值。置信椭圆可以提供更直观的异常值检测结果。

程序设计

• 完整程序和数据私信博主回复：PCA马氏距离异常值检测（Matlab）。

参考资料

[1] https://blog.csdn.net/kjm13182345320/article/details/124864369
[2] https://blog.csdn.net/kjm13182345320/article/details/127896974?spm=1001.2014.3001.5502