【高阶数据结构(四)】图的最短路径问题

💓博主CSDN主页:杭电码农-NEO💓

⏩专栏分类:高阶数据结构专栏⏪

🚚代码仓库:NEO的学习日记🚚

🌹关注我🫵带你学习更多数据结构
🔝🔝

在这里插入图片描述

高阶数据结构

1. 前言
2. 单源最短路径问题
3. dijkstra算法讲解
4. bellman-Ford算法讲解
5. 多源最短路径问题
6. Floyd-Warshall算法讲解
7. 总结

1. 前言

关于图论,无非就是最小生成树问题和最短路径问题. 对于最短路径问题来说, 分为单源最短路径和多源最短路径, 并且图中的权值是否有负数, 对应能使用的算法也不同

本章重点:

本篇文章着重讲解图的单源最短路径之Dijkstra算法和bellman-Ford算法.以及多源最短路径之Floyd-wars hall算法. 文章会着重讲解这些算法的思路, 代码实现部分要靠大家的理解能力了

2. 单源最短路径问题

所谓的单源最短路径,也就是从图中任意一点出发, 到图中每个节点的最短路径,也就是最小的权值和

在这里插入图片描述

对于单源最短路径的求解. 我们一般使用输出型参数. 用两个数组来表示最短路径的权值以及最短路径的路径.

//存储任意点到图中其他点的最短路径的权值vector<W>& dist//记录srci->其他顶点最短路径父顶点数组vector<int>& parentPath

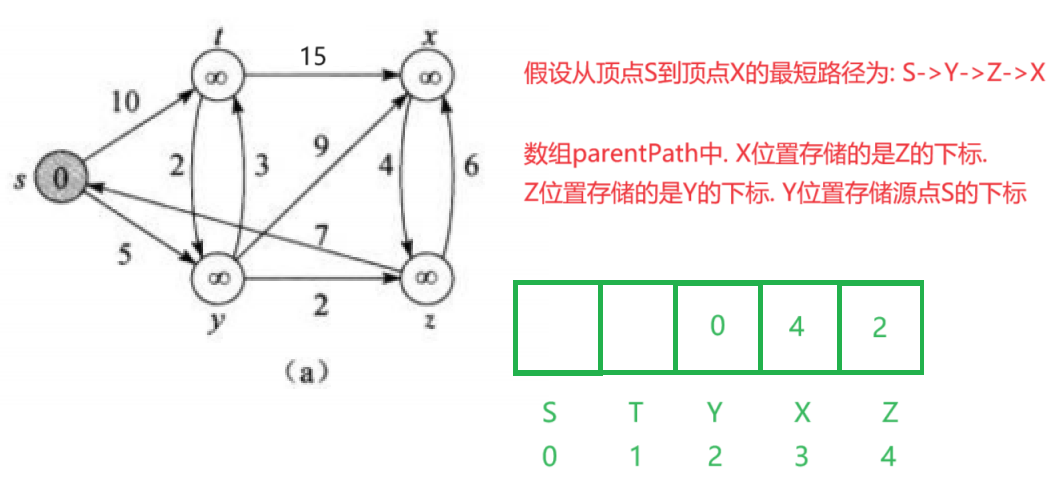
第一个数组很好理解. 图中的顶点会简化成为数组中的元素. 所以dist数组中的dist[i]=j.代表顶点i到srci的最短路径的权值. 不好理解的是第二个数组. 它存储的是最短路径的父顶点. 什么意思呢? 请看下图:

在这里插入图片描述

3. dijkstra算法讲解

针对一个带权有向图G，将所有结点分为两组S和Q，S是已经确定最短路径的结点集合，在初始时为空（初始时就可以将源节点s放入，毕竟源节点到自己的代价是0），Q 为其余未确定最短路径的结点集合，每次从Q 中找出一个起点到该结点代价最小的结点u ，将u 从Q 中移出，并放入S 中，对u 的每一个相邻结点v 进行松弛操作。

松弛即对每一个相邻结点v ，判断源节点s到结点u 的代价与u 到v 的代价之和是否比原来s 到v 的代价更小，若代价比原来小则要将s 到v 的代价更新为s 到u 与u 到v 的代价之和，否则维持原样。如此一直循环直至集合Q 为空，即所有节点都已经查找过一遍并确定了最短路径，至于一些起点到达不了的结点在算法循环后其代价仍为初始设定的值，不发生变化

定义很抽象,现在来看看实图:

在这里插入图片描述

从S开始,s->y是最短路径了, 就以y为起点(y的值被更新为5)更新与y相连的t,z,x. 同时s->t也被更新为10. y->t小于s->t. 所以将t重新更新为8. x,z也是同理. 第二次更新完. s->z最短.就以z为起点更新与z相连的x.以此类推.直到所有顶点都在集合S中.

话不多说,上代码:

void Dijkstra(const V& src, vector<W>& dist, vector<int>& pPath)//Dijkstra算法求解最短路径,两个数组,一个存储两个点之间的最小权值(从src点,到图中其他的点),另一个存父路径节点下标
{size_t srci = GetIndex(src);size_t n = _vertex.size();dist.resize(n, MAX_W);pPath.resize(n, -1);dist[srci] = W();pPath[srci] = srci;vector<bool> check(n, false);//此数组中存放已经确定了的最短路劲的节点for(int j=0;j<n;j++)//n个节点,一共会更新n次,也可以判断check数组中的元素是否全为true{//选最短路径的顶点更新其他路径(不在s中)int u = 0;//最小的点的下标W minu = MAX_W;//最小的点的权值for (int i = 0; i < n; i++)//选择dist数组中权值最小的,作为起始点来进行松弛操作{if (check[i] == false && dist[i] < minu){u = i;minu = dist[i];check[i] = true;}}//进行松弛更新,srci->u, u->其他顶点(v), srci->v就可以更新出来for (int v = 0; v < n; v++)//从0到n,把与u点相连的所有顶点都找出来更新{if (_edge[u][v] != MAX_W && dist[u] + _edge[u][v] < dist[v])//若srci->u+u->v的距离小于dist[v]的大小,则更新他{dist[v] = dist[u] + _edge[u][v];pPath[v] = u;}}}
}

此算法只适用于不带负权路径的图
若有不懂,欢迎私信

4. bellman-Ford算法讲解

Dijkstra算法只适用于不带负权路径的图, 具体的原因可以参考这篇文章: 负权路径带来的后果

显而易见, bellman算法可以解决带负权路径的图

说白了此算法就是一个暴力求解的过程, 它的时间复杂度是O(N^3). 它的思路就是以所有顶点为起始点,更新所有相连的边

在这里插入图片描述

更新次序就是(t，z)，(t，y)，(t，z)，(y,x)，(y，z), (z,x), (z，s), (s,t), (s,y). 更新(y,z)时,由于更新后的值是7+9=16>2,所以不会更新这条边. 其他更新边也是同理. 但是这样暴力更新一次并不能解决问题,因为假如只更新一次, (s,t)的值就是6, 但是显而易见, s->y->x->t的权值是2,要小于6. 出现这种情况的原因是, 还没有以x为起始点进行更新其他点时, 根本就不知道x->t这条路. 所以我们需要以所有点为起始点更新n次,n是顶点的数量

上代码:

bool BellmanFord(const V& src, vector<W>& dist, vector<int>& pPath)//贝尔曼-福特算法求解最短路径
{size_t srci = GetIndex(src);size_t n = _vertex.size();dist.resize(n, MAX_W);pPath.resize(n, -1);dist[srci] = W();//用i->j,图中的所有边去更新for (int k = 0; k < n; k++)//再套一层循环的原因是,只更新一轮可能会有问题,更新K轮一定不会有问题{bool check = false;for (int i = 0; i < n; i++){for (int j = 0; j < n; j++){if (_edge[i][j] != MAX_W && dist[i] + _edge[i][j] < dist[j])//若这条边存在,并且从i->j要少于直接0->j{dist[j] = dist[i] + _edge[i][j];pPath[j] = i;check = true;}}}if (check == true) breal;}//有可能K轮循环后,会形成闭环return true;
}

很明显它的时间复杂度是O(N^3)

5. 多源最短路径问题

说白了就是任意两点之间的最短路径
Floyd-Warshall算法就是解决方法之一

和单源最短路径算法的思路相似. 这里需要用到两个数组, 只不过这里是用两个二维数组, 一个二维数组存储顶点i->j的最短路径值, 另外一个数组存储 (i,j)的父节点下标. i,j是最短路径的中间某节点

6. Floyd-Warshall算法讲解

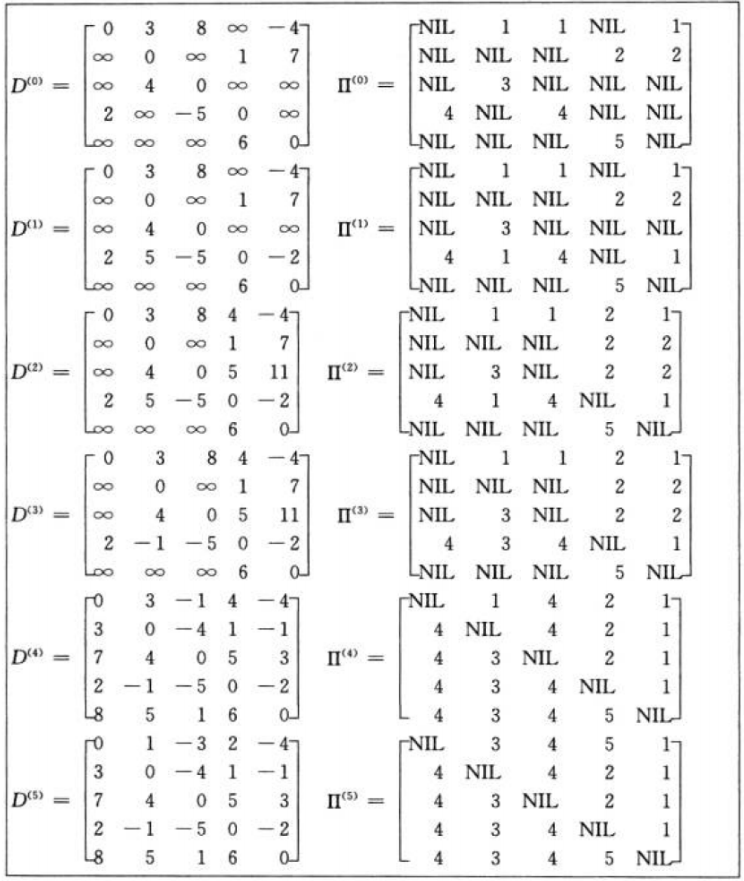
Floyd算法考虑的是一条最短路径的中间节点，即简单路径p={v1,v2,…,vn}上除v1和vn的任意节
点。设k是p的一个中间节点，那么从i到j的最短路径p就被分成i到k和k到j的两段最短路径p1，p2。p1是从i到k且中间节点属于{1，2，…，k-1}取得的一条最短路径。p2是从k到j且中间节点属于{1，2，…，k-1}取得的一条最短路径

在这里插入图片描述

你可能觉得很抽象,下面来个实际案例:

在这里插入图片描述

上代码:

void FloydWarShall(vector<vector<W>>& vvDist, vector<vector<int>>& vvpPath)//多源最短路径求解问题(任意两点的最短路径),数组vvDist中包含了所有点的最短距离
{size_t N = _vertex.size();vvDist.resize(N);vvpPath.resize(N);for (int i = 0; i < N; i++){vvDist[i].resize(N, MAX_W);vvpPath[i].resize(N, -1);}//把直接相连的边给更新一下,后续就不需要_edge数组了for (int i = 0; i < N; i++){for (int j = 0; j < N; j++){if (_edge[i][j] != MAX_W)//直接相连{vvDist[i][j] = _edge[i][j];vvpPath[i][j] = i;//起点是i,目前的父路径暂时是i(后面可能会是K)}if (i == j)vvDist[i][j] = W();}}//最短路径的更新,i->j,中间可能经过了k个顶点,i->{其他顶点(最多是N-2)}->j//k作为i,j的中间点,k可以是任意顶点,k可以是1,2,3,任意点,要把所有点拿来更新for (int k = 0; k < N; k++)//虽然是最多只需要走n-2个点,但是这里除掉的两个点我们并不知道是哪两个,所以都需要走一遍{for (int i = 0; i < N; i++){for (int j = 0; j < N; j++){//以K作为中间的去更新i->j的路径if (vvDist[i][k] != MAX_W && vvDist[k][j] != MAX_W && vvDist[i][k] + vvDist[k][j] < vvDist[i][j])//i->k的路径和k->j的路径都存在,并且i->k加上k->j的路径小于i直接到j{vvDist[i][j] = vvDist[i][k] + vvDist[k][j];vvpPath[i][j] = vvpPath[k][j];//这里j的父路径不能直接写成k,因为k->j中间可能还有其他点,比如k->x->y->j,最开始的i,j是在_edge数组中取得,而这里应该是从vvppath[k][j]中取得,需要找跟j相连的上一个顶点}}}}
}