旅行商从城市1出发,终点城市由算法求解而定
部分代码
close all
clear
clc
global data
load('data.txt')%导入TSP数据集
Dim=size(data,1)-1;%维度
lb=-100;%下界
ub=100;%上界
fobj=@Fun;%计算总距离
SearchAgents_no=100; % 种群大小(可以修改)
Max_iteration=1000; % 最大迭代次数(可以修改)
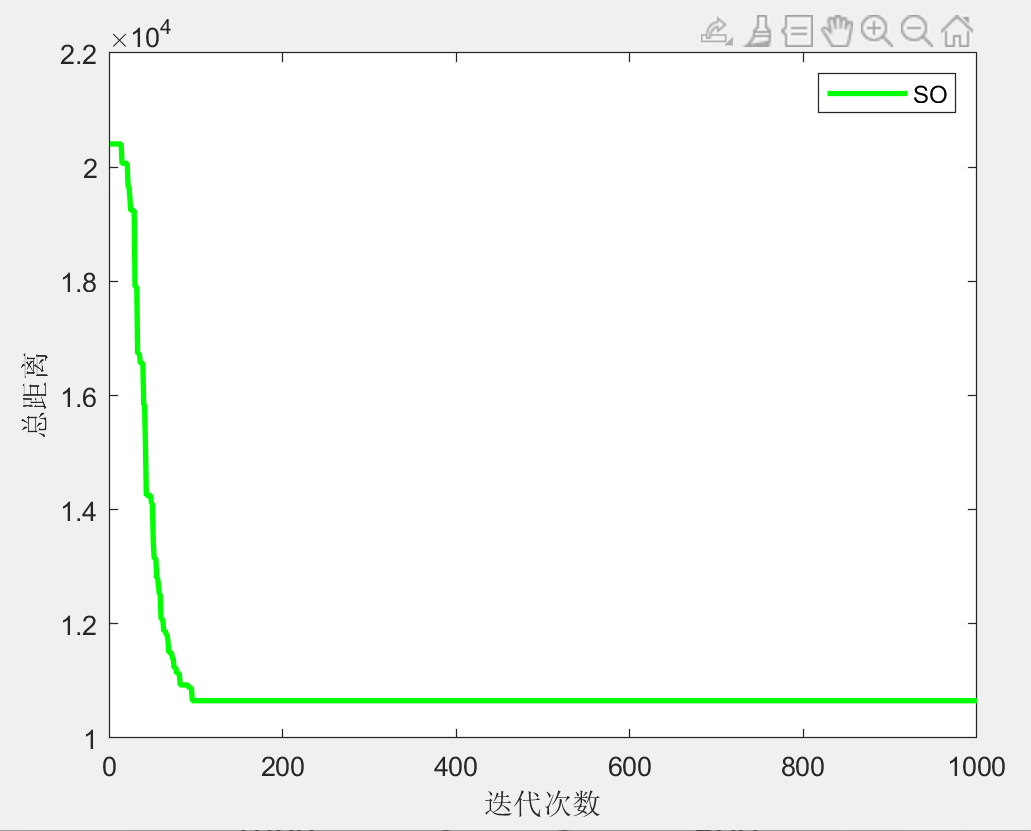
%% 画收敛曲线图
figure
plot(curve,'g-','linewidth',2)
xlabel('迭代次数')
ylabel('总距离')
legend('SO')
%% 显示结果
fprintf('算法得到的路径:%d',Kd(1))
for i=2:length(Kd)fprintf(' > %d',Kd(i));
end
fprintf('\n');
display(['算法求解的总路径总长:' num2str(curve(end))]);
%% 保存数据
dlmwrite('Kd.txt',Kd,'delimiter', '\n')%保留最终的城市序列
dlmwrite('curve.txt',curve,'delimiter', '\n')%保留算法求解的收敛曲线
部分结果
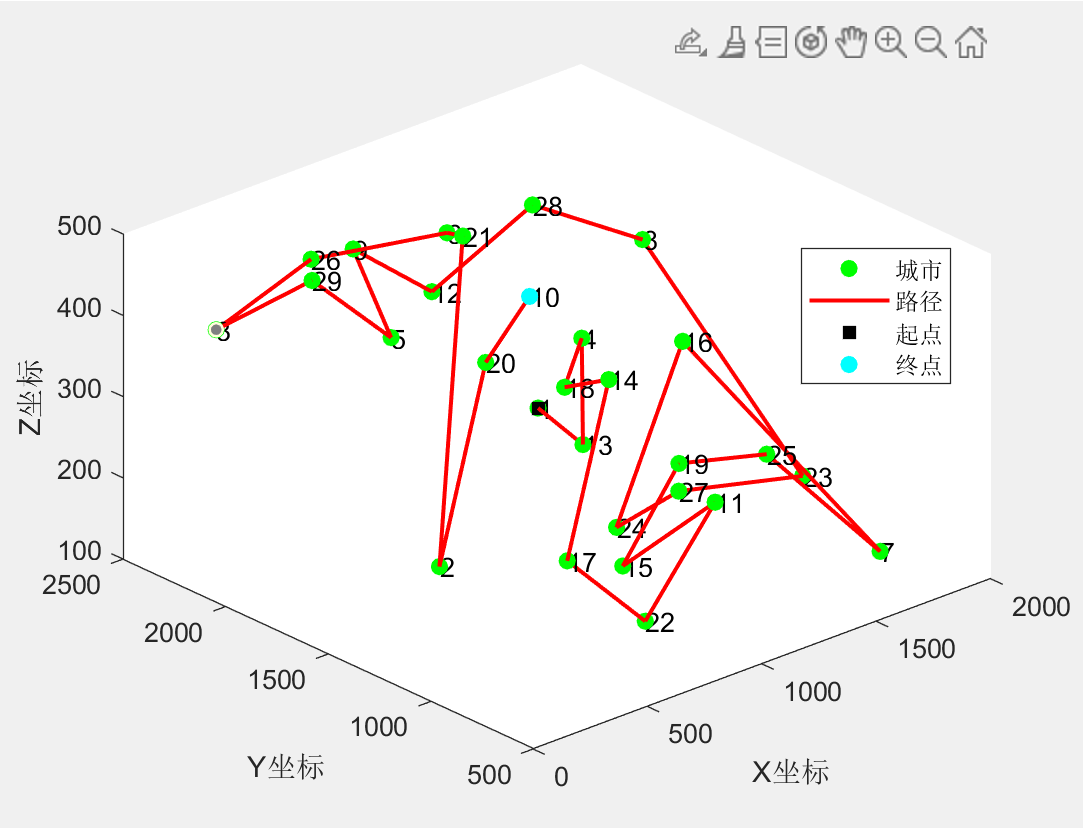
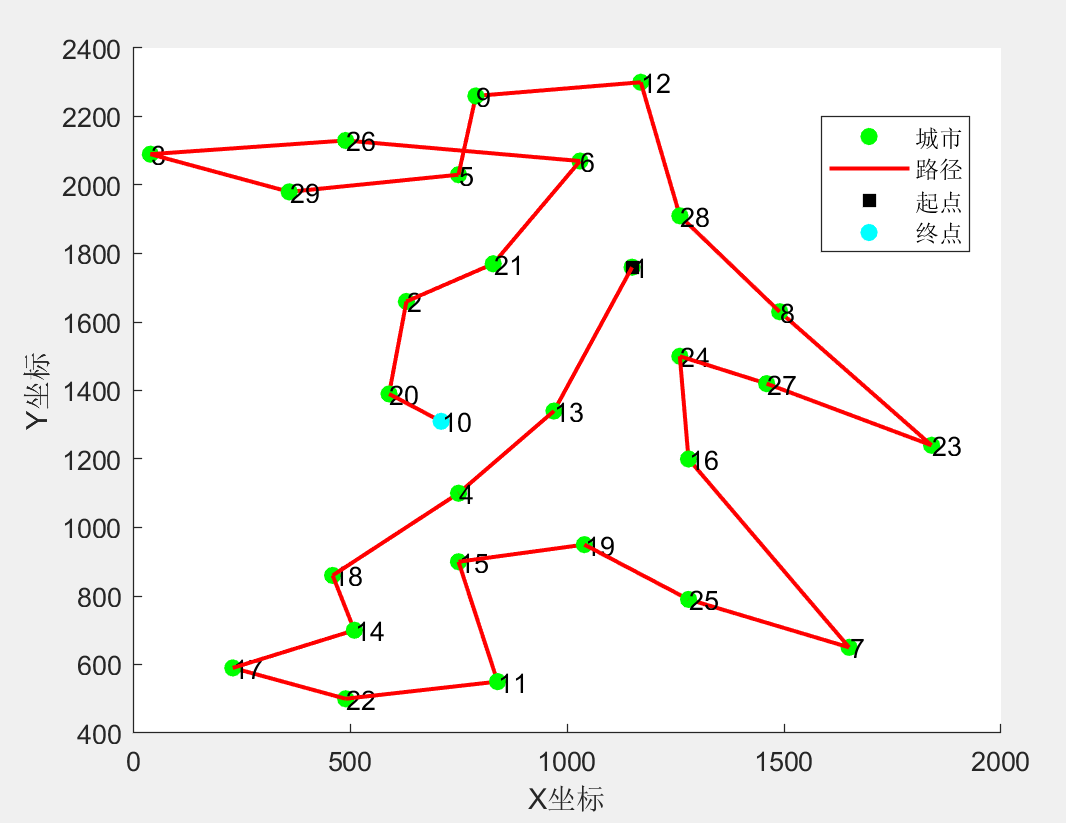
算法得到的路径:1 > 13 > 4 > 18 > 14 > 17 > 22 > 11 > 15 > 19 > 25 > 7 > 16 > 24 > 27 > 23 > 8 > 28 > 12 > 9 > 5 > 29 > 3 > 26 > 6 > 21 > 2 > 20 > 10
算法求解的总路径总长:10653.3976
完整MATLAB代码
不闭合三维TSP:蛇优化算法SO求解不闭合三维TSP(起点固定,终点不定,可以更改数据集),MATLAB代码
点击main.m即可运行





![[机缘参悟-185] - 《道家-水木然人间清醒1》读书笔记 - 真相本质 -8- 认知觉醒 - 逻辑谬误、认知偏差:幸存者偏差](https://img-blog.csdnimg.cn/direct/545c424cc62e4d66bfc12829c8708ca1.png)