ZISUOJ 数据结构--图及其应用

说明

        主要考察建图，图的遍历以及求最小生成树。都还是比较简单的，后面就直接上代码了。

        最小生成树采用prim还是kruskal算法要看题目怎么给出数据，如果以邻接矩阵的形式给出，采用prim算法比较合适，如果以边和边的权重的形式给出，则采用kruskal算法比较合适。例如这里的D和E题采用kruskal算法比较好，但是不代表用prim算法不能做，我这两个题给出的就是prim的解法，但是某些题用另一个算法极不方便，因此还是建议采用题目所暗示我们应使用的方法最佳。

题目列表

问题 A: 图的遍历—深度优先搜索—邻接矩阵

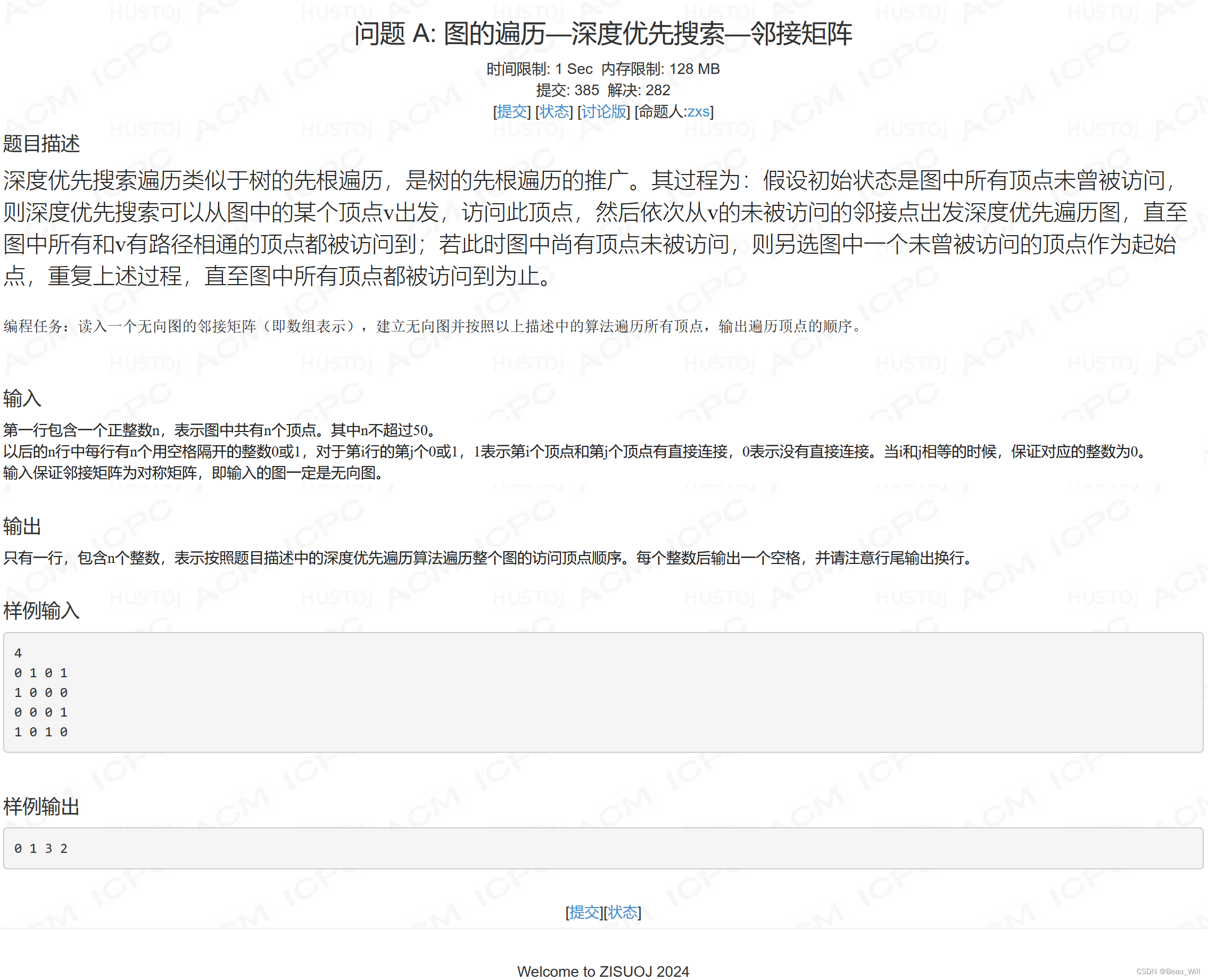
参考题解：

#include <iostream>
#include <functional>int main(){std::cin.tie(nullptr)->sync_with_stdio(false);constexpr int MAX_N = 5e1+5;int g[MAX_N][MAX_N] {};bool vis[MAX_N] {};int n;std::cin >> n;for(int i = 0;i<n;i++){for(int j = 0;j<n;j++){std::cin >> g[i][j];}}using Dfs = std::function<void(int)>; Dfs dfs = [&](int u) {std::cout << u << ' ';for(int i = 0;i<n;i++){if(g[u][i]&&!vis[i]) vis[i]=true,dfs(i);}};vis[0] = true;dfs(0);std::cout << '\n';return 0;
}

问题 B: 图的遍历—DFS—已知边

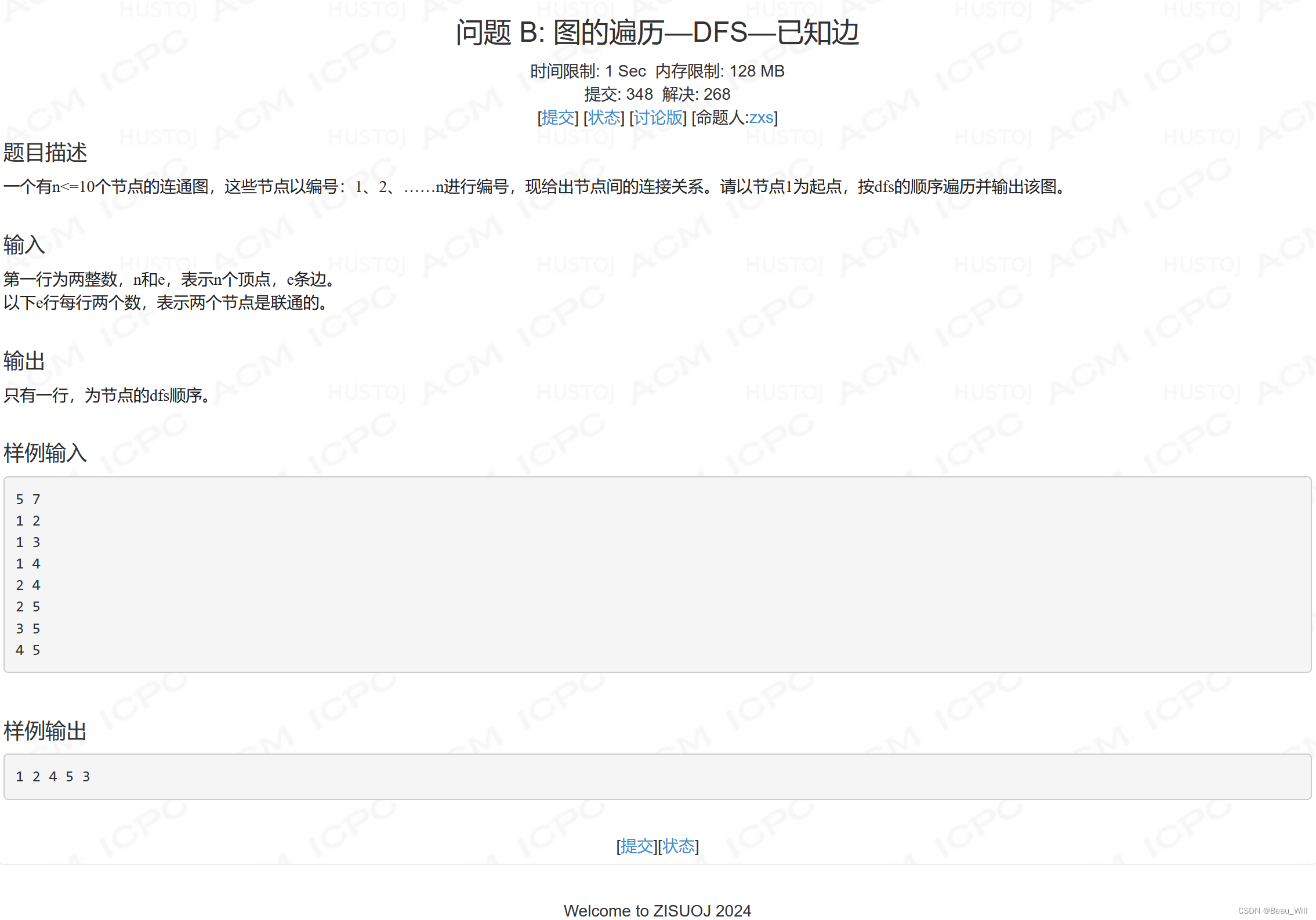
参考题解：

#include <iostream>
#include <functional>int main(){std::cin.tie(nullptr)->sync_with_stdio(false);constexpr int MAX_N = 1e1+5;int g[MAX_N][MAX_N] {};bool vis[MAX_N] {};int n,m;std::cin >> n >> m;while(m--){int x,y;std::cin >> x >> y;g[x][y]=g[y][x]=1;}using Dfs = std::function<void(int)>;Dfs dfs = [&](int u){std::cout << u << ' ';for(int i = 1;i<=n;i++){if(g[u][i]&&!vis[i]) vis[i]=true,dfs(i);}};vis[1] = true;dfs(1);std::cout << '\n';return 0;
}

问题 C: 图的遍历—广度优先搜索

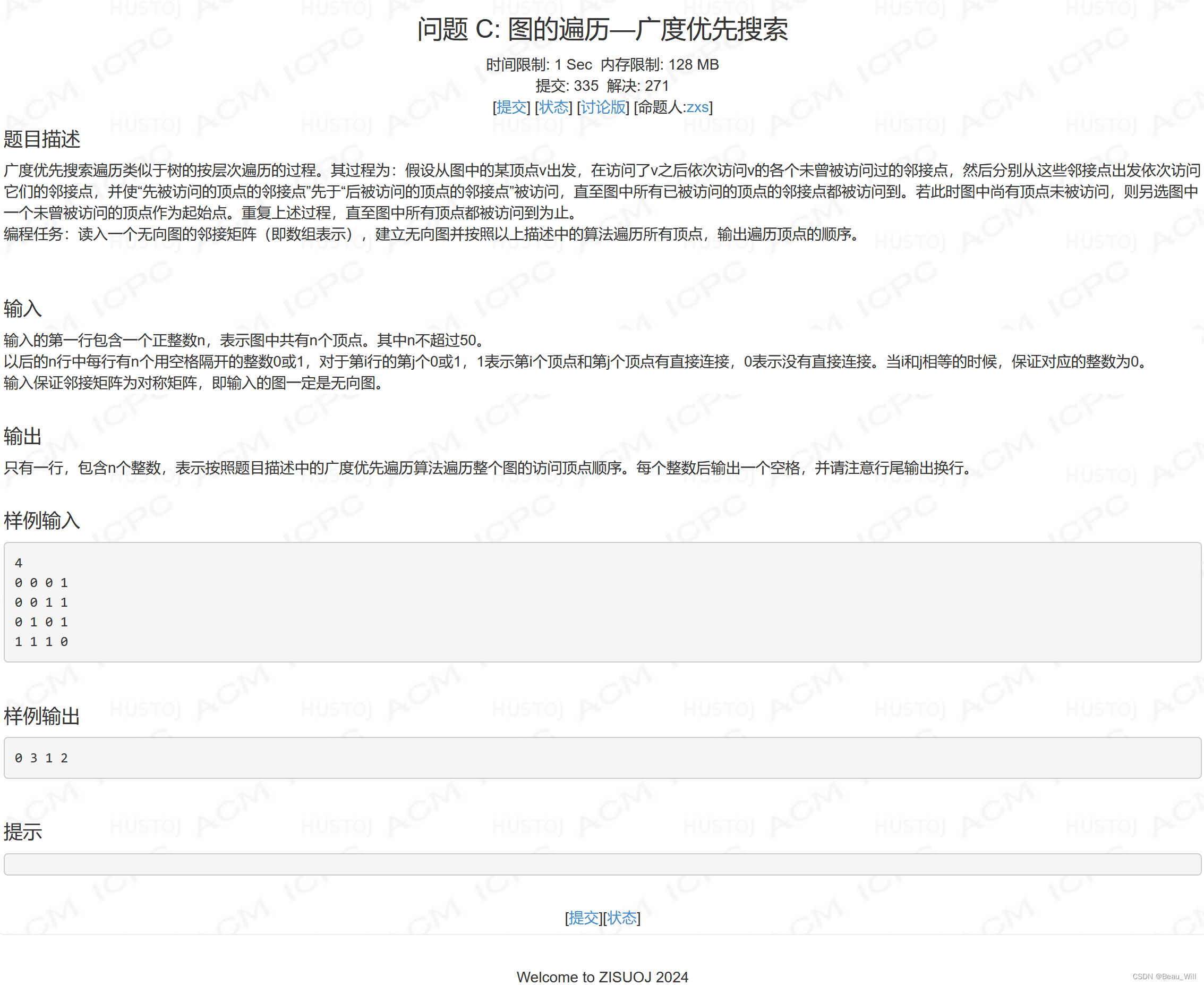
参考题解：

#include <iostream>
#include <queue>int main(){std::cin.tie(nullptr)->sync_with_stdio(false);constexpr int MAX_N = 5e1+5;int g[MAX_N][MAX_N] {};bool vis[MAX_N] {};int n;std::cin >> n;for(int i = 0;i<n;i++){for(int j = 0;j<n;j++){std::cin >> g[i][j];}}auto bfs = [&](){std::queue<int> q;q.emplace(0);vis[0] = true;while(!q.empty()){auto t = q.front();q.pop();std::cout << t << ' ';for(int i = 0;i<n;i++){if(!vis[i]&&g[t][i]){vis[i] = true;q.emplace(i);}}}};bfs();std::cout << '\n';return 0;
}

问题 D: 最小生成树-局域网

 

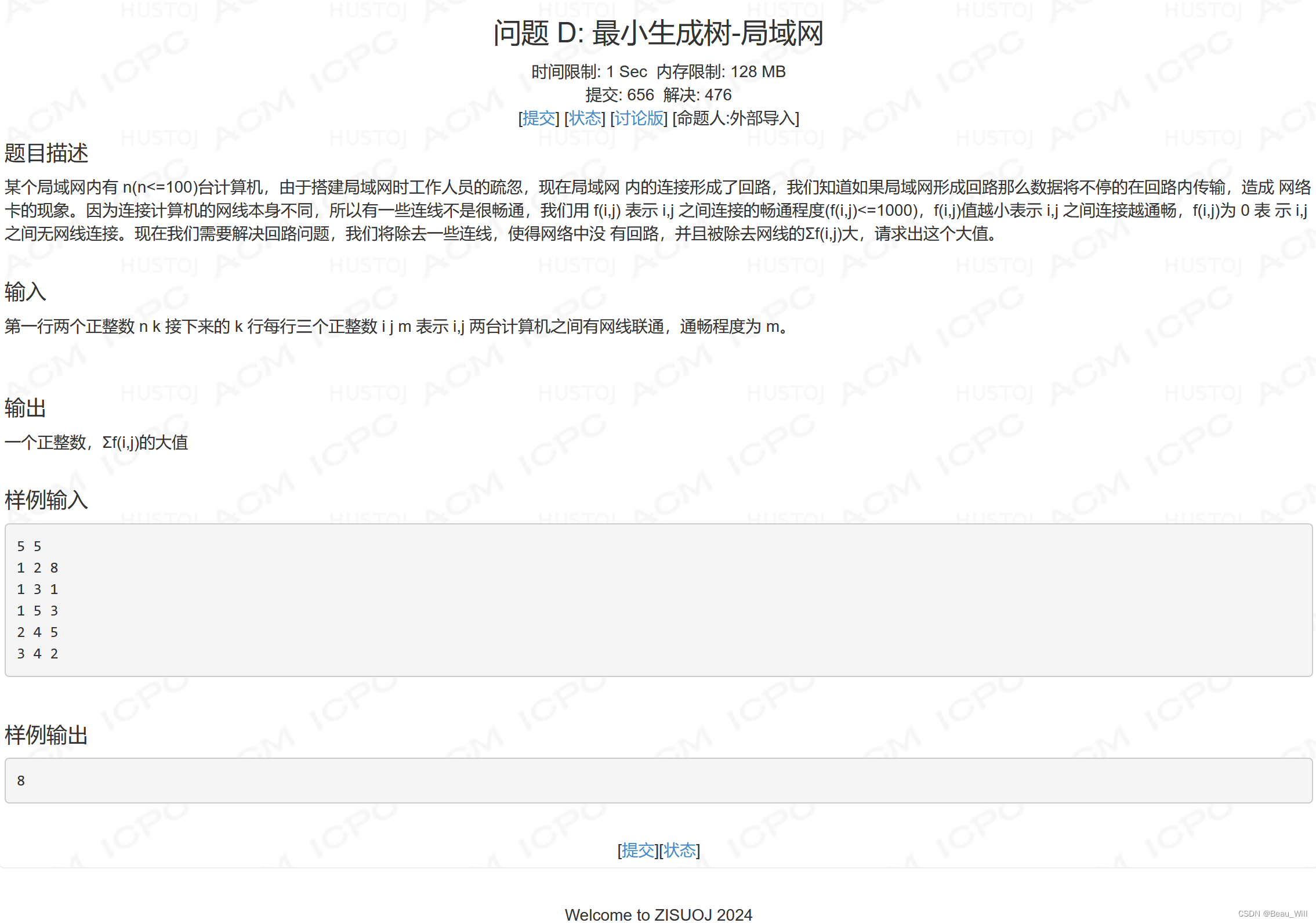
参考题解：

#include <iostream>
#include <cstring>
#include <type_traits>
template<typename T1,typename T2>
typename std::common_type<T1,T2>::type min(T1 num1,T2 num2){return num1>num2?num2:num1;
}
int main(){std::cin.tie(nullptr)->sync_with_stdio(false);constexpr int MAX_N = 1e2+5,INF = 0x3f3f3f3f;int g[MAX_N][MAX_N];int dist[MAX_N];memset(g,0x3f,sizeof g);bool vis[MAX_N] = {false};int n,m;std::cin >> n >> m;int ans = 0;while(m--){int x,y,w;std::cin >> x >> y >> w;g[x][y]=g[y][x]=min(g[y][x],w);ans+=w;}auto prim = [&]()->int{memset(dist,0x3f,sizeof dist);dist[1] = 0;int ans = 0;for(int i = 0;i<n;++i){int t = -1;for(int j = 1;j<=n;++j){if(!vis[j]&&(t==-1||dist[t]>dist[j])) t = j;}if(dist[t]==INF) return INF;ans+=dist[t];vis[t] = true;for(int j = 1;j<=n;++j) dist[j] = min(dist[j],g[t][j]);}return ans;};ans-=prim();std::cout << ans << '\n';return 0;
}

问题 E: 最小生成树-繁忙的都市

 

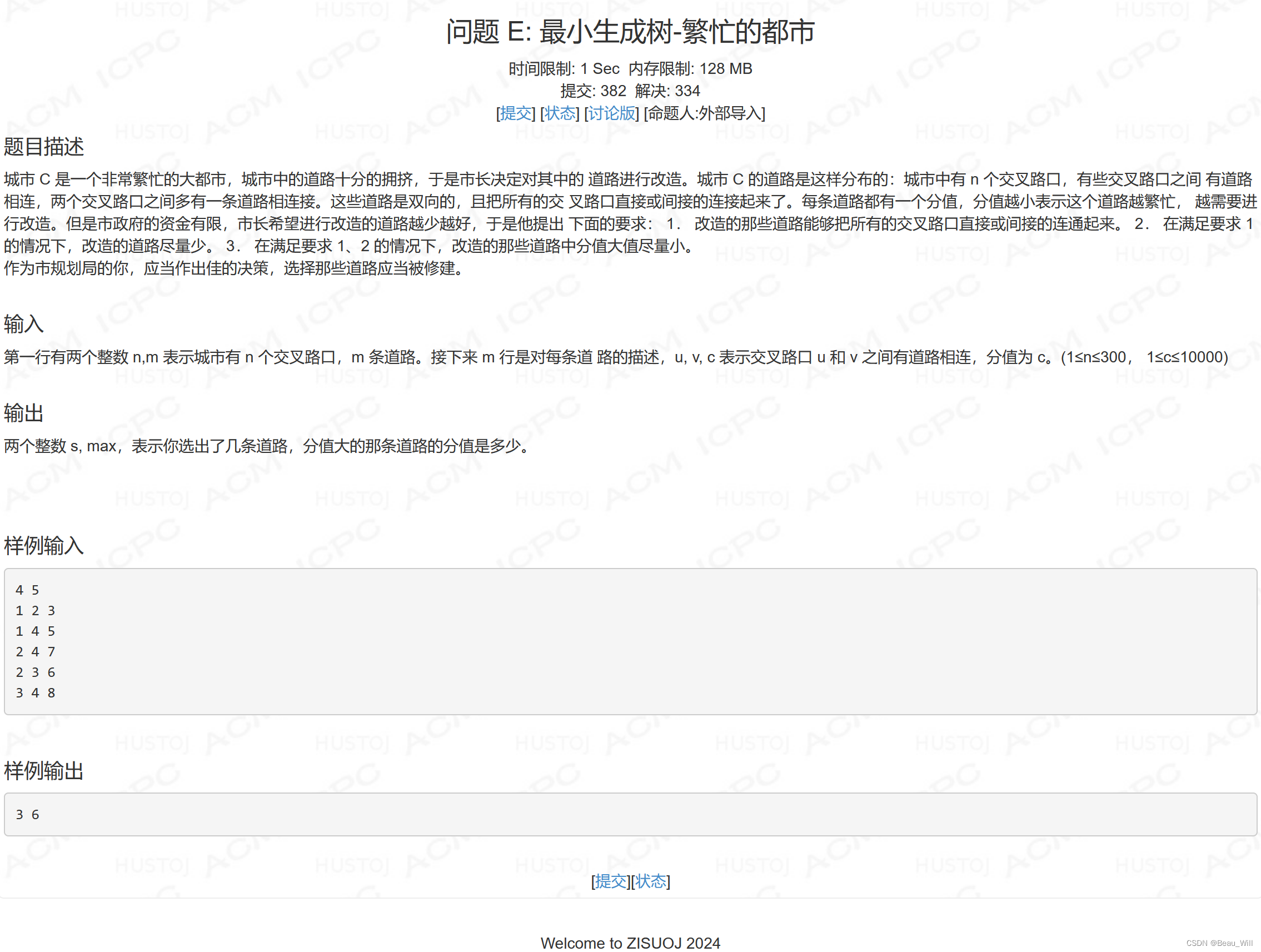
参考题解：

#include <iostream>
#include <cstring>
#include <type_traits>
template<typename T1,typename T2>
typename std::common_type<T1,T2>::type max(T1 num1,T2 num2){return num1<num2?num2:num1;
}
template<typename T1,typename T2>
typename std::common_type<T1,T2>::type min(T1 num1,T2 num2){return num1>num2?num2:num1;
}
int main(){std::cin.tie(nullptr)->sync_with_stdio(false);constexpr int MAX_N = 1e2+5,INF = 0x3f3f3f3f;int g[MAX_N][MAX_N];int dist[MAX_N];memset(g,0x3f,sizeof g);bool vis[MAX_N] = {false};int n,m;std::cin >> n >> m;while(m--){int x,y,w;std::cin >> x >> y >> w;g[x][y]=g[y][x]=min(g[y][x],w);}auto prim = [&]()->int{memset(dist,0x3f,sizeof dist);dist[1] = 0;int ans = 0;for(int i = 0;i<n;++i){int t = -1;for(int j = 1;j<=n;++j){if(!vis[j]&&(t==-1||dist[t]>dist[j])) t = j;}if(dist[t]==INF) return INF;ans = max(ans,dist[t]);vis[t] = true;for(int j = 1;j<=n;++j) dist[j]=min(dist[j],g[t][j]);}return ans;};std::cout << n-1 << ' ' << prim() << '\n';return 0;
}

问题 F: 最小生成树-联络员

 

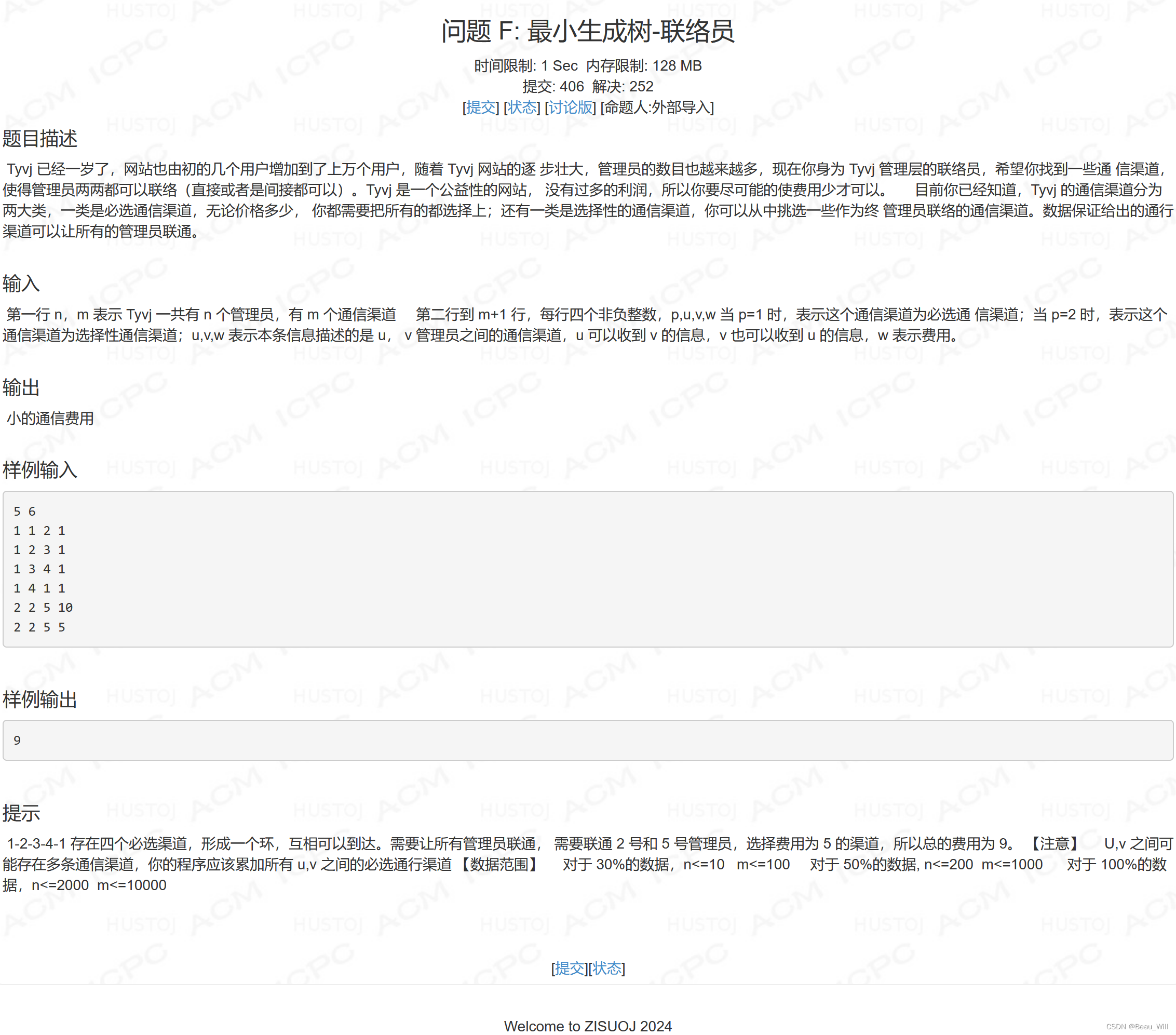
参考题解：

#include <iostream>
#include <vector>
#include <functional>
#include <algorithm>constexpr int MAX_N = 2e3+5,MAX_M = 1e4+5,INF = 0x3f3f3f3f;struct edge{int x,y,w;bool operator < (const edge& W){return w<W.w;}edge(int _x,int _y,int _w):x(_x),y(_y),w(_w){}
};
std::vector<edge> edges;
int fa[MAX_N];
int main(){std::cin.tie(nullptr)->sync_with_stdio(false);int n,m;std::cin >> n >> m;for(int i = 1;i<=n;++i) fa[i] = i;using Find = std::function<int(int)>;Find find = [&](int x){if(x!=fa[x]) fa[x] = find(fa[x]);return fa[x];};int ans = 0;while(m--){int t,x,y,w;std::cin >> t >> x >> y >> w;if(t==1){ans+=w;fa[find(x)] = find(y);}else{edges.emplace_back(x,y,w);}}auto kruskal = [&](){std::sort(edges.begin(),edges.end());for(int i = 0;i<edges.size();++i){int fx = find(edges[i].x),fy = find(edges[i].y),w = edges[i].w;if(fx!=fy){fa[fx] = fy;ans+=w;}}};kruskal();std::cout << ans << '\n';return 0;
}

问题 G: 最小生成树-连接格点

 

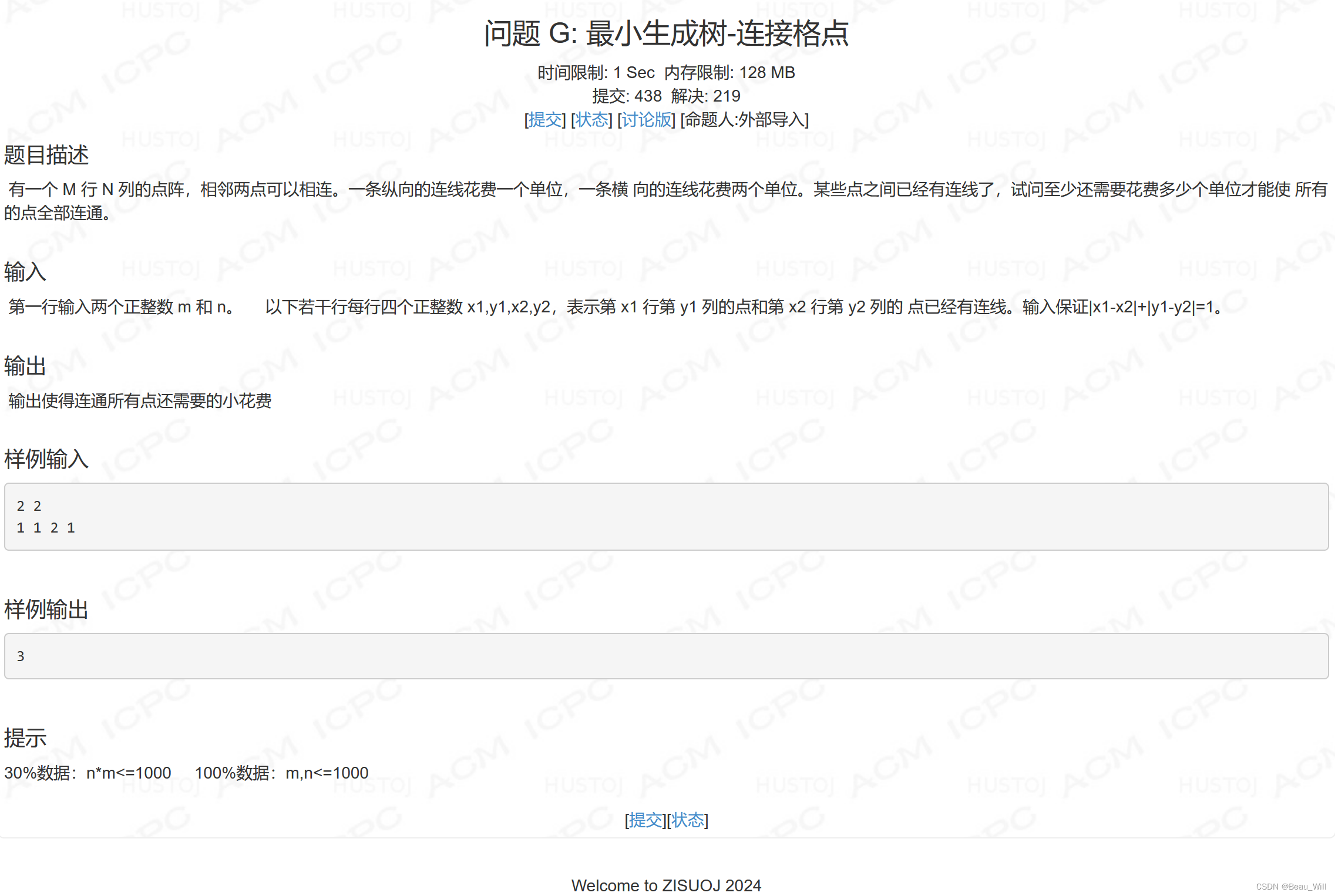
参考题解：

#include <iostream>
#include <functional>constexpr int MAX_N = 1e3+5;int fa[MAX_N*MAX_N];int main(){std::cin.tie(nullptr)->sync_with_stdio(false);using Find = std::function<int(int)>;Find find = [&](int x)->int{if(x!=fa[x]) fa[x] = find(fa[x]);return fa[x];};int n,m;std::cin >> n >> m;for(int i = 0;i<=n*m;++i) fa[i] = i;int x1,y1,x2,y2;while(std::cin >> x1 >> y1 >> x2 >> y2){fa[find((x1-1)*m+y1)] = find((x2-1)*m+y2);}int ans = 0;auto kruskal = [&]()->void{for(int i = 1;i<n;++i){for(int j = 1;j<=m;++j){int dx = find((i-1)*m+j),dy = find(i*m+j);if(dx!=dy){++ans;fa[dx] = dy;}}}for(int i = 1;i<=n;++i){for(int j = 1;j<m;++j){int dx = find((i-1)*m+j),dy = find((i-1)*m+j+1);if(dx!=dy){ans+=2;fa[dx] = dy;}}}};kruskal();std::cout << ans << '\n';return 0;
}

问题 H: 最小生成树-最短网络

 

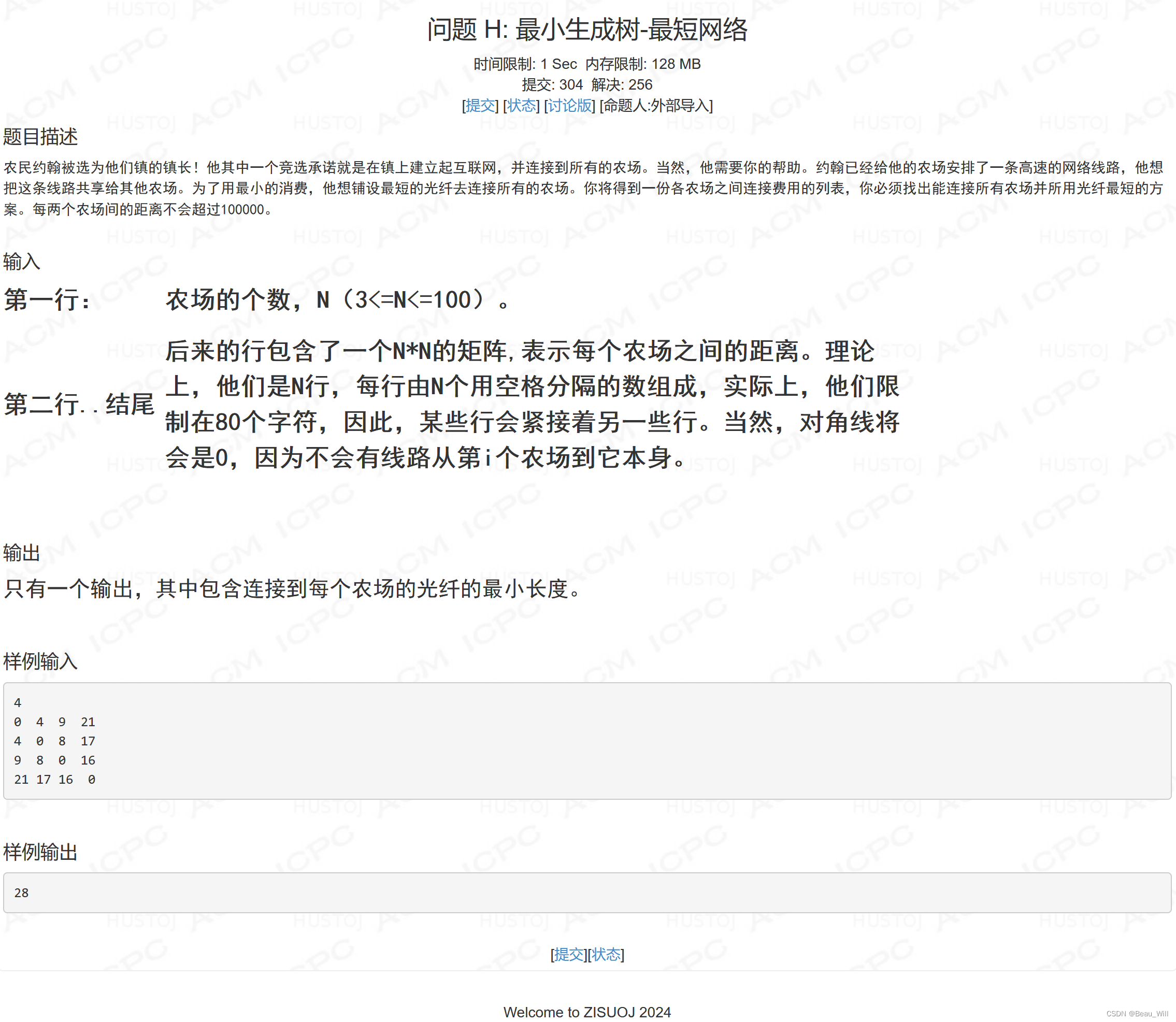
参考题解：

#include <iostream>
#include <cstring>
#include <type_traits>
template<typename T1,typename T2>
typename std::common_type<T1,T2>::type min(T1 num1,T2 num2){return num1>num2?num2:num1;
}
int main(){std::cin.tie(nullptr)->sync_with_stdio(false);constexpr int MAX_N = 1e2+5,INF = 0x3f3f3f3f;int g[MAX_N][MAX_N];int dist[MAX_N];bool vis[MAX_N] {};int n;std::cin >> n;for(int i = 1;i<=n;++i){for(int j = 1;j<=n;++j){std::cin >> g[i][j];}}auto prim = [&]()->int{memset(dist,0x3f,sizeof dist);int res = 0;dist[1] = 0;for(int i = 0;i<n;++i){int t = -1;for(int j = 1;j<=n;++j){if(!vis[j]&&(t==-1||dist[j]<dist[t])) t = j;}if(dist[t]==INF) return INF;vis[t] = true;res+=dist[t];for(int j = 1;j<=n;++j) dist[j]=min(dist[j],g[t][j]);}return res;};std::cout << prim() << '\n';return 0;
}

问题 I: 最小生成树-最优布线问题

 

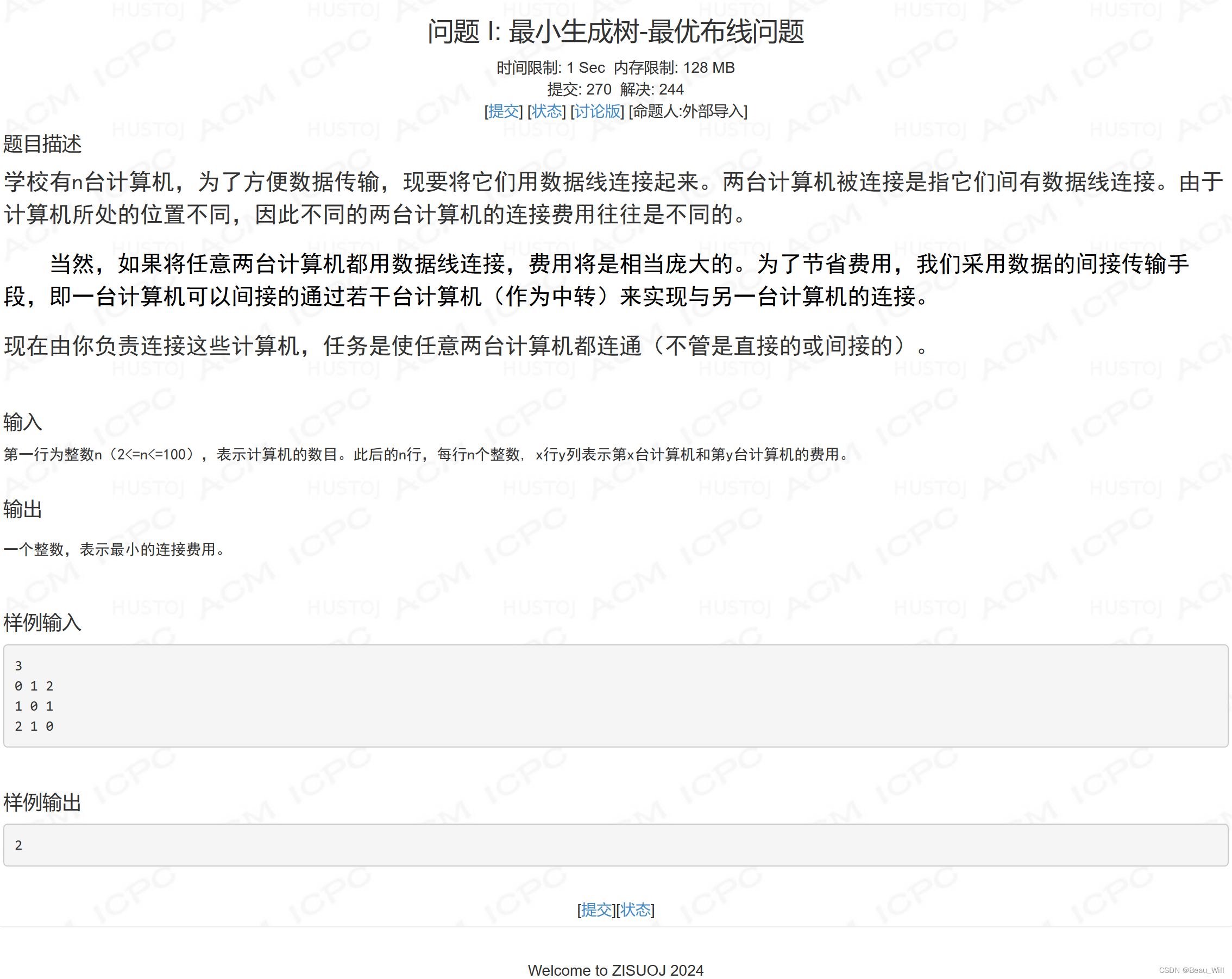
参考题解：

#include <iostream>
#include <cstring>
#include <type_traits>
template<typename T1,typename T2>
typename std::common_type<T1,T2>::type min(T1 num1,T2 num2){return num1>num2?num2:num1;
}
int main(){std::cin.tie(nullptr)->sync_with_stdio(false);constexpr int MAX_N = 1e2+5,INF = 0x3f3f3f3f;int g[MAX_N][MAX_N];int dist[MAX_N];bool vis[MAX_N] {};int n;std::cin >> n;for(int i = 1;i<=n;++i){for(int j = 1;j<=n;++j){std::cin >> g[i][j];}}auto prim = [&]()->int{memset(dist,0x3f,sizeof dist);int res = 0;dist[1] = 0;for(int i = 0;i<n;++i){int t = -1;for(int j = 1;j<=n;++j){if(!vis[j]&&(t==-1||dist[j]<dist[t])) t = j;}if(dist[t]==INF) return INF;vis[t] = true;res+=dist[t];for(int j = 1;j<=n;++j) dist[j]=min(dist[j],g[t][j]);}return res;};std::cout << prim() << '\n';return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.rhkb.cn/news/329523.html

如若内容造成侵权/违法违规/事实不符，请联系长河编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

docker三种自定义网络(虚拟网络) overlay实现原理

docker三种自定义网络(虚拟网络) overlay实现原理

docker提供了三种自定义网络驱动&#xff1a;bridge、overlay、macvlan。 bridge驱动类似默认的bridge网络模式。 overlay和macvlan是用于创建跨主机网络。 支持自定义网段、网关&#xff0c;docker network create --subnet 172.77.0.0/24 --gateway 172.77.0.1 my_n…
阅读更多...
浅谈JMeter测试计划

浅谈JMeter测试计划

浅谈JMeter测试计划 创建测试计划 当启动JMeter后&#xff0c;默认进入界面会看到一个测试计划 测试计划组件详情 在上述界面中&#xff0c;我们可以看到测试计划的组成为名称、注释、用户定义的变量、独立运行每个线程组、主线程结束后运行tearDown线程组、函数测试模式以…
阅读更多...
科技查新中查新点的怎样进行精确提炼？

科技查新中查新点的怎样进行精确提炼？

根据2015年《科技查新技术规范》&#xff1a;科技查新简称查新&#xff0c;以反映查新项目主题内容的查新点为依据&#xff0c;以计算机检索为主要手段&#xff0c;以获取密切相关文献为检索目标&#xff0c;运用综合分析和对比方法&#xff0c;对查新项目的新颖性做出文献评价…
阅读更多...
JMETER工具：以录制手机app为例

JMETER工具：以录制手机app为例

JMETER工具&#xff1a;以录制手机app为例子 JMETER安装和环境配置 pc需要安装jdk&#xff0c;并进行jdk的环境配置&#xff0c;安装好jdk并配置好后&#xff0c;通过命令行输入java –version出现以下界面就表示安装成功&#xff1a; &#xff08;对应的jdk版本不可太低&…
阅读更多...
深度学习——图像分类（CNN）—训练模型

深度学习——图像分类（CNN）—训练模型

训练模型 1.导入必要的库2.定义超参数3.读取训练和测试标签CSV文件4.确保标签是字符串类型5.显示两个数据框的前几行以了解它们的结构6.定义图像处理参数7.创建图像数据生成器8.设置目录路径9.创建训练和验证数据生成器10.构建模型11.编译模型12.训练模型并收集历史13.绘制损失…
阅读更多...
excel转pdf并且加水印，利用ByteArrayOutputStream内存流不产生中间文件

excel转pdf并且加水印，利用ByteArrayOutputStream内存流不产生中间文件

首先先引入包&#xff1a;加水印和excel转PDF的 <dependency><groupId>com.itextpdf</groupId><artifactId>itextpdf</artifactId><version>5.5.12</version></dependency><dependency><groupId>org.apache.poi&l…
阅读更多...
jenkins插件之xunit

jenkins插件之xunit

安装jenkins插件 搜索xunit并安装 项目配置 配置 - Build Steps 您的项目 - 配置 - Build Steps, 新增 Run with timeout 超时时间根据实际情况配置 Build Step选择 执行SHELL 填写一下命令&#xff0c;这个命令是docker中执行phpunit单元测试&#xff0c;请根据你的实际…
阅读更多...
FPGA学习笔记之Nios II（一）简单介绍及新建工程及下载

FPGA学习笔记之Nios II（一）简单介绍及新建工程及下载

系列文章目录 文章目录 系列文章目录前言QsysNios IIhello world 实例Platform DesignNios II程序设计 前言 利用Quartus中的Qsys工具&#xff0c;可以实现在FPGA里面跑嵌入式的功能 Qsys Altera 公司将主控制器、数字信号处理模块、存储器及其控制模块、各种接口协议等模块&…
阅读更多...
亚马逊测评还能做吗？

亚马逊测评还能做吗？

只能说测评不是唯一的手段&#xff0c;但是推销量的一把好手。首先测评能让listing快速成长&#xff0c;短期内有望成为爆款&#xff0c;速度快&#xff0c;利润高&#xff0c;回款快。相对其他推广&#xff0c;测评无疑是有效&#xff0c;省培养listing的方法。其次新品前期太…
阅读更多...
聊聊 JSON Web Token (JWT) 和 jwcrypto 的使用

聊聊 JSON Web Token (JWT) 和 jwcrypto 的使用

哈喽大家好&#xff0c;我是咸鱼。 最近写的一个 Python 项目用到了 jwcrypto 这个库&#xff0c;这个库是专门用来处理 JWT 的&#xff0c;JWT 全称是 JSON Web Token &#xff0c;JSON 格式的 Token。 今天就来简单入门一下 JWT。 官方介绍&#xff1a;https://jwt.io/intr…
阅读更多...
RH850F1KM-S4-100Pin_ R7F7016453AFP MCAL Gpt 配置

RH850F1KM-S4-100Pin_ R7F7016453AFP MCAL Gpt 配置

1、Gpt组件包含的子配置项 GptDriverConfigurationGptDemEventParameterRefsGptConfigurationOfOptApiServicesGptChannelConfigSet2、GptDriverConfiguration 2.1、GptAlreadyInitDetCheck 该参数启用/禁用Gpt_Init API中的GPT_E_ALREADY_INITIALIZED Det检查。 true:开启Gpt_…
阅读更多...
JS核心语法【流程控制语句、函数】；DOM【查找元素、操作元素、事件】--学习JavaEE的day48

JS核心语法【流程控制语句、函数】；DOM【查找元素、操作元素、事件】--学习JavaEE的day48

day48 JS核心技术 JS核心语法 继day47 注意&#xff1a;用到控制台输出、弹窗 流程控制语句 If else、For、For-in(遍历数组时&#xff0c;跟Java是否一样【java没有】)、While、Do while、break、continue 案例&#xff1a; 1.求1-100之间的偶数之和 <!DOCTYPE html> …
阅读更多...
Android消息机制回顾（Handler、Looper、MessageQueue源码解析）

Android消息机制回顾（Handler、Looper、MessageQueue源码解析）

回顾&#xff1a; Android消息机制 Android消息机制主要指的是Handler的运行机制以及Handler所附带的MessageQueue和Looper的工作机制。 介绍 通过Handler 消息机制来解决线程之间通信问题&#xff0c;或者用来切换线程。特别是在更新UI界面时&#xff0c;确保了线程间的数…
阅读更多...
5.23 学习总结

5.23 学习总结

一.项目优化&#xff08;语音通话&#xff09; 实现步骤&#xff1a; 1.用户发送通话申请&#xff0c;并处理通话请求&#xff0c;如果同意&#xff0c;为两个用户之间进行连接。 2.获取到电脑的麦克风和扬声器&#xff0c;将获取到的语音信息转换成以字节数组的形式传递。 …
阅读更多...
基于FPGA的图像直方图均衡化处理verilog实现,包含tb测试文件和MATLAB辅助验证

基于FPGA的图像直方图均衡化处理verilog实现,包含tb测试文件和MATLAB辅助验证

目录 1.算法运行效果图预览 2.算法运行软件版本 3.部分核心程序 4.算法理论概述 5.算法完整程序工程 1.算法运行效果图预览 FPGA的仿真图如下&#xff1a; 将数据导入MATLAB&#xff0c;对比结果如下&#xff1a; 2.算法运行软件版本 MATLAB2022a vivado2019.2 3.部分…
阅读更多...
【Android安全】AOSP版本对应编号| AOSP版本适配Pixel或Nexus型号 | 驱动脚本下载地址

【Android安全】AOSP版本对应编号| AOSP版本适配Pixel或Nexus型号 | 驱动脚本下载地址

AOSP版本对应编号 https://source.android.com/docs/setup/about/build-numbers?hlzh-cn#source-code-tags-and-builds 例如android-8.1.0_r1 对应的编号是OPM1.171019.011 可以适配Pixel 2 XL AOSP驱动脚本下载 编译AOSP时&#xff0c;需要Google的驱动&#xff0c;后面才…
阅读更多...
Jenkins 构建 Maven 项目：项目和服务器在一起的情况

Jenkins 构建 Maven 项目：项目和服务器在一起的情况

bash.sh内容 #!/bin/bash#删除历史数据 rm -rf ruoyi-admin.jar# appname$1 appnamevideo.xxxxx.com #获取传入的参数 echo "arg:$appname"#获取正在运行的jar包pid # pidps -ef | grep $1 | grep java -jar | awk {printf $2} pidps -ef | grep $appname | grep ja…
阅读更多...
高铁VR虚拟全景展示提升企业实力和形象

高铁VR虚拟全景展示提升企业实力和形象

步入VR的神奇世界&#xff0c;感受前所未有的汽车展示体验。VR虚拟现实技术以其独特的沉浸式模拟&#xff0c;让你仿佛置身于真实展厅之中&#xff0c;尽情探索汽车的每一处细节。 一、定制化展示&#xff0c;随心所欲 VR汽车虚拟展厅打破空间束缚&#xff0c;让汽车制造商能够…
阅读更多...
从零开始傅里叶变换

从零开始傅里叶变换

从零开始傅里叶变换 1 Overview2 傅里叶级数2.1 基向量2.2 三角函数系表示 f ( t ) f(t) f(t)2.2.1 三角函数系的正交性2.2.2 三角函数系的系数 2.3 复指数函数系表示 f ( t ) f(t) f(t)2.3.1 复指数函数系的系数2.3.2 复指数函数系的正交性 2.4 傅里叶级数总结 3 傅里叶变换…
阅读更多...
基于轻量级神经网络GhostNet开发构建CIFAR100数据集场景下的图像识别分析系统，对比不同分辨路尺度下模型的性能情况

基于轻量级神经网络GhostNet开发构建CIFAR100数据集场景下的图像识别分析系统，对比不同分辨路尺度下模型的性能情况

Cifar100数据集是一个经典的图像分类数据集&#xff0c;常用于计算机视觉领域的研究和算法测试。以下是关于Cifar100数据集的详细介绍&#xff1a; 数据集构成&#xff1a;Cifar100数据集包含60000张训练图像和10000张测试图像。其中&#xff0c;训练图像分为100个类别&#x…
阅读更多...
最新文章
推荐文章

Copyright @ 2022~2023