声明:文章是从本人公众号中复制而来,因此,想最新最快了解各类智能优化算法及其改进的朋友,可关注我的公众号:强盛机器学习,不定期会有很多免费代码分享~
目录
原始算术优化算法
改进点1:引入余弦控制因子的动态边界策略
改进点2:自适应t分布变异策略
改进算法流程图
结果展示
参考文献
完整代码获取
很多小伙伴问我,某某算法到底该怎么改效果比较好。实话讲,如果不经过实验,我随便说一个策略,效果能好吗?至于加什么策略,怎么加策略,为什么加这个策略,都是需要经过实验才能得出来的。
对于那些初学智能优化算法的小伙伴,我的建议还是要多看论文进行学习和复现。相信没有小伙伴是不看文献直接就能想出来创新点的吧,如果有,那大概率是闭门造车。
当然,我相信大部分小伙伴代码水平没那么高,复现论文仍有一定难度。因此,我也会不断推出一些复现改进算法的文章。大家也可以用这些改进的算法应用到各类预测、优化、故障诊断、路径优化等等任务中,我之前的推文里也有很多,都可以套用。
今天为大家带来一篇北大核心+CSCD扩展上的一篇论文完美复现。这是一篇是2022年发表在《计算机应用研究》上的一篇文章,级别还是很高的,改进的算法叫算术优化算法。
原始算术优化算法
算术优化算法也是一种新颖的2021年提出的基于群体的元启发式算法,包括勘探阶段和开发阶段。勘探阶段的算子为乘法M(Multiplication) 和除法D(Division) ,这两个算子(D和M) 分散性高,有利于全局勘探;而开发阶段的算子为加法A( Addition) 和减法S(Subtraction),这两个算子(A和S)具有显著的低分散性,可以容易地接近目标,因此S和A的联系来支持开发阶段,有利于更快地接近最优解。
为了避免推文中出现繁冗的公式,这边仅仅列出公式及其序号,方便大家在后续改进过程中查看公式序号从而对应改进点。
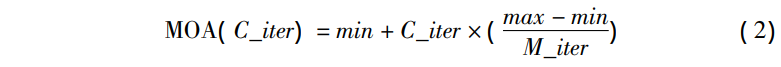
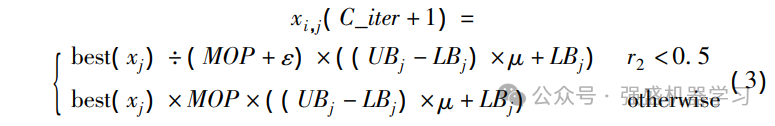
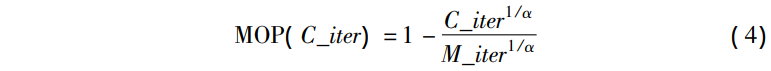

不得不说,原始AOA算法操作简单且寻优时间较短,同时寻优精度良好,超过了大部分传统启发式算法,但仍存在易陷入局部最优等问题。
针对这些问题,文章提出了一种自适应t分布变异和动态边界策略改进的算术优化算法(t-CAOA)。
这是2022年发表在《计算机应用研究》上的一篇文章,级别还是很高的,改进的算法叫算术优化算法。
改进点1:引入余弦控制因子的动态边界策略
与其他群智能优化算法类似,基本算术优化算法在寻优过程中同样会遇到全局搜索能力和局部开发能力不平衡的现象。在基本算术优化算法中,MOA的取值决定了算法优化过程中的阶段选择,MOA越大,算法的局部搜索能力越强;MOA越小,算法的全局搜索能力越强,式(2)描述的MOA是线性增长的,即算法的全局搜索能力线性减小。然而,AOA在进化探索过程中却是非线性变化的,线性增长的MOA不能准确贴近实际迭代过程,引入余弦控制因子将MOA的变化转换为非线性,可以更贴近算法实际的迭代过程,以下将引入余弦控制因子的自适应系数命名为CMOA。引入余弦控制因子的CMOA在算法迭代前期,CMOA较小并缓慢增大以充分进行全局搜索;在算法后期,CMOA急速增大以进行局部搜索。AOA作为一种新型群体智能算法,如何平衡其全局搜索和局部搜索对提高算法的性能至关重要。若全局搜索和局部搜索协调不好,在进化过程中可能会导致算法出现早熟收敛现象。因此,本文在MOA更新公式中加入由余弦因子控制的非线性惯性权重来动态调节算法全局搜索与局部搜索的平衡,提高算法寻优精度和稳定性。公式如下:
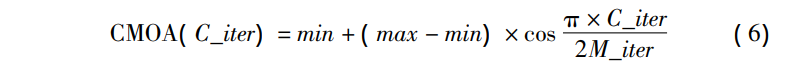
改进点2:自适应t分布变异策略
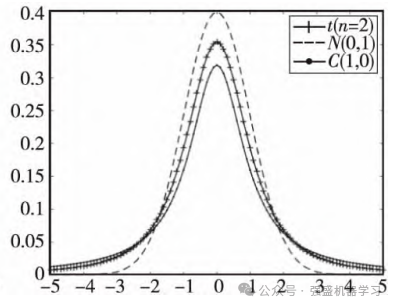
t分布又称学生分布,含有参数自由度,当t(n→∞)→N(0,1),当t(n=1)=C(0,1),其中N(0,1)为高斯分布,C(0,1)为柯西分布,即标准高斯分布和柯西分布是t分布的两个边界特例分布,三者函数的分布图像如下图所示。其中,柯西变异的全局搜索能力较强,能够有效地保持种群的多样性;而高斯变异的局部开发能力较强,可以保证进化后期的收敛速度。t分布综合了柯西分布和高斯分布的优点,本文采用以迭代次数iter为t分布的自由度参数的t分布变异算子对解的位置进行扰动,使得算法在迭代前期具有较好的全局开发能力,在迭代后期具有良好的局部探索能力,并提高算法的收敛速度,具体的位置更新方式如下:
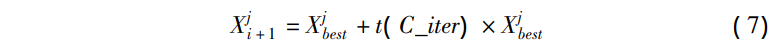
其中:Xji+1为自适应t分布变异扰动后最优解在第j维的位置;Xjbest为变异扰动前最优解在第j维的位置,迭代次数作为t分布的自由度参数。
改进算法流程图
t-CAOA的具体执行流程如下图所示:
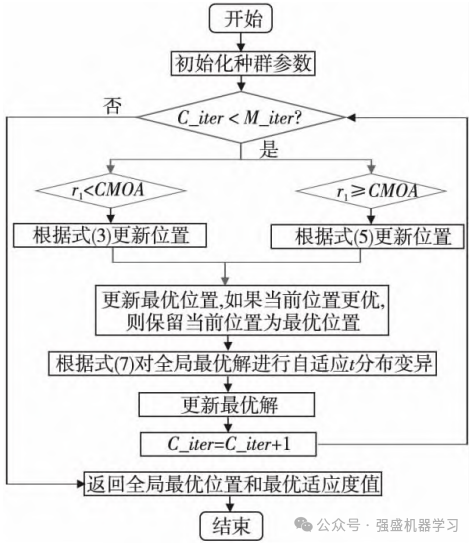
1)初始化参数,包括种群规模为30,迭代次数为500;
2)随机生成初始解和计算适应度值;
3)根据式(6)更新CMOA的参数值,使得勘探和开发阶段之间的转换动态且非线性;
4)若r1<CMOA,根据式(3)实行勘探并更新位置;若r1≥CMOA,根据式(5)实行开发并更新位置。
结果展示
原文作者选取了 10 个不同特点的基准测试函数与基本算术优化算法AOA、海洋捕食者算法MPA、灰狼优化算法GWO、鲸鱼优化算法WOA进行对比。
这边为了方便大家对比,选取23个基准测试函数,与基本算术优化算法AOA进行对比。


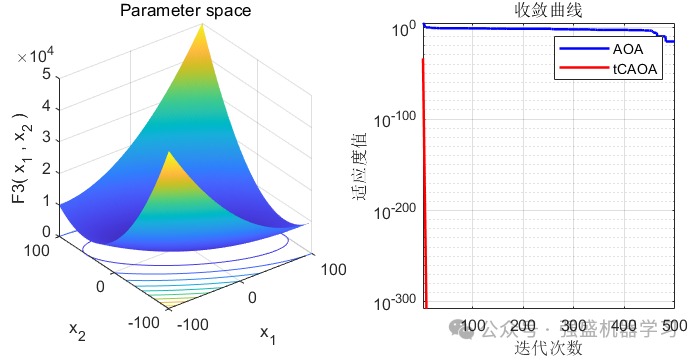
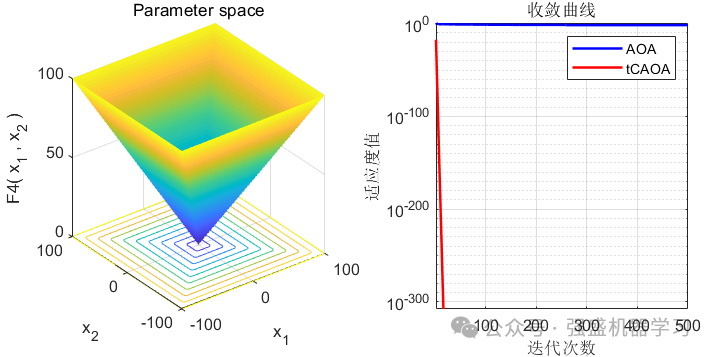



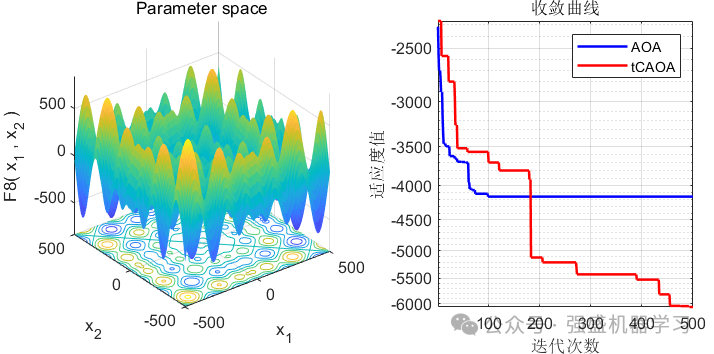
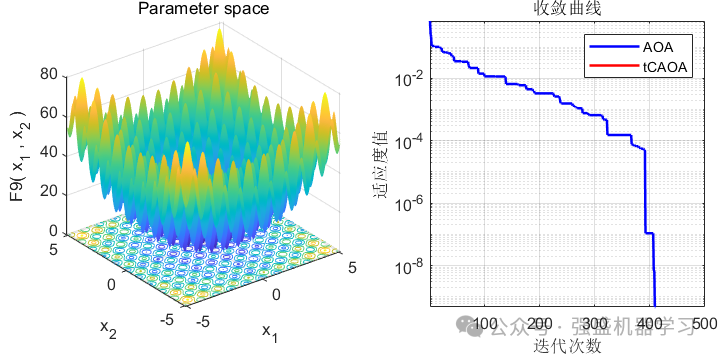
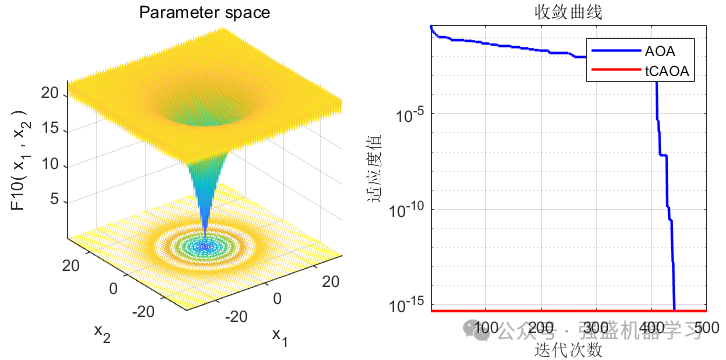
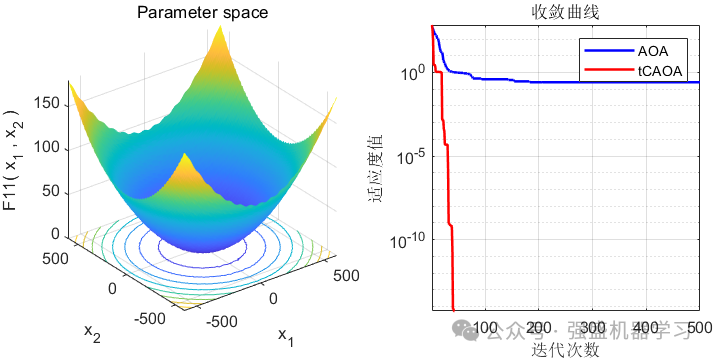
可以看到,选取的前11个函数里(没有故意遗漏!),在大部分函数上都优于原来的AOA算法,且收敛速度大幅提高,是一种不错的改进方法!
当然,部分函数上该算法已经直接找到最优值,如F9,因此迭代曲线上没有显示(至于这种策略好不好仁者见仁智者见智,由于不是我改进的方法我这边不做过多评判)。
其他的函数小伙伴们可以自行尝试,总体上效果明显优于原有的算术优化算法!
参考文献
[1]郑婷婷,刘升,叶旭.自适应t分布与动态边界策略改进的算术优化算法[J].计算机应用研究,2022,39(05):1410-1414.
完整代码获取
点击下方小卡片,后台回复关键字,不区分大小写:
TCAOA
其他更多需求或想要的代码均可点击下方小卡片后后台私信,看到后会秒回~
更多代码链接:更多代码链接




![[数组查找]1.图解线性查找及其代码实现](https://img-blog.csdnimg.cn/direct/849e0bba932747fe83a56d0aa18bad82.png)