【C语言】二叉树的实现

文章目录

  • 前言
  • ⭐一、二叉树的定义
  • 🚲二、创建二叉树
  • 🎡三、二叉树的销毁
  • 🎉四、遍历二叉树
    • 1. 前序遍历
    • 2. 中序遍历
    • 3. 后序遍历
    • 4. 层序遍历
  • 🌲五、二叉树的计算
    • 1. 计算二叉树结点个数
    • 2. 计算二叉树叶子结点的个数
    • 3. 计算二叉树的深度
    • 4. 计算二叉树第k层的结点个数
    • 5. 查找二叉树中值为x的结点
    • 6. 判断二叉树是否为完全二叉树
  • 🏝️六、整体代码展示

前言

在学习二叉树实现时，我们首先要对二叉树基本认识有一定的了解，下面我总结了以下几点有关二叉树的性质以及特点：
🎈每一个节点最多有两棵子树，不存在度大于2的节点。
🎈左右子树是有顺序的，其次序不能颠倒。
🎈二叉树一般有四种形态，分别为：空二叉树，只有一个根节点，根结点只有左子树和根节点只有右子树。
🎈二叉树常用的三种性质：1)二叉树的第 i 层上最多有2 ^ (i - 1)个节点；
2)深度为K的二叉树最多有2 ^ (k - 1)个节点。
3)度为0的节点个数比度为2的节点个数多一个。

⭐一、二叉树的定义

二叉树通常以结构体的形式定义，其结构体内容包括三部分：本节点所存储的值、左孩子节点的指针以及右孩子节点的指针。这里需要注意，子节点必须使用指针，就像我们定义结构体链表一样，下一个节点必须使用地址的方式存在在结构体当中。

typedef int BTDateType;typedef struct BinaryTreeNode
{BTDateType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;

🚲二、创建二叉树

当我们对二叉树的掌握还不够深入时，我们也可以创建一棵简单的二叉树，减少时间成本。

// 手搓一个二叉树
BTNode* BuyNode(int x)
{BTNode* node = (BTNode*)malloc(sizeof(BTNode));if (node == NULL){perror("malloc fail");return NULL;}node->data = x;node->left = NULL;node->right = NULL;
}BTNode* CreatBinaryTree()
{BTNode* node1 = BuyNode(1);BTNode* node2 = BuyNode(2);BTNode* node3 = BuyNode(3);BTNode* node4 = BuyNode(4);BTNode* node5 = BuyNode(5);BTNode* node6 = BuyNode(6);node1->left = node2;node1->right = node4;node2->left = node3;node4->left = node5;node4->right = node6;return node1;
}

而真正的二叉树创建的过程是这样的：首先给出一个数组，将要创建的元素放在数组里。然后通过遍历（前 或 中 或 后序遍历）的顺序访问并创建二叉树每个节点，最后返回根节点的地址即创建完成。
我们假设通过前序序列的方式访问并创建二叉树：

// 创建树,按前序遍历的顺序
BTNode* BinaryTreeCreate(BTDateType* a, int* pi) {if (a[*pi] != '#') // '#'代表叶子结点{BTNode* root = (BTNode*)malloc(sizeof(BTNode));root->data = a[*pi];(*pi)++;root->left = BinaryTreeCreate(a, pi);(*pi)++;root->right = BinaryTreeCreate(a, pi);return root;}else {return NULL;}
}

🎡三、二叉树的销毁

// 销毁
void BinaryTreeDestory(BTNode* root)
{if (root){BinaryTreeDestory(root->left);BinaryTreeDestory(root->right);free(root);root = NULL;}
}

🎉四、遍历二叉树

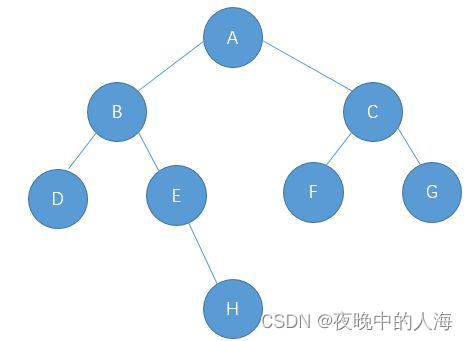
在这里插入图片描述
前序遍历，中序遍历和后序遍历，实际上就是指根节点在子节点的先中后的顺序不同。以上图为例：
前序序列：A、B、D、E、H、C、F、G

中序遍历：D、B、H、E、A、F、C、G

后序遍历：D、H、E、B、F、G、C、A

这三种遍历方式，在代码上面还是非常相似的，只不过递归的顺序不同。

1. 前序遍历

先遍历根结点，再遍历左子树，最后遍历右子树。

// 前序遍历
void PrevOrder(BTNode* root)
{if (root == NULL){printf("N "); //打印空节点数据return;}printf("%d ", root->data); // 输出节点数据PrevOrder(root->left); //递归遍历左子树节点的数据PrevOrder(root->right); //递归遍历右子树节点的数据
}

2. 中序遍历

先遍历左子树，再遍历根结点，最后遍历右子树。

// 中序遍历
void InOrder(BTNode* root)
{if (root == NULL){printf("N "); //打印空节点数据return;}InOrder(root->left); //递归遍历左子树节点的数据printf("%d ", root->data); //输出节点数据InOrder(root->right); //递归遍历右子树节点的数据
}

3. 后序遍历

先遍历左子树，再遍历右子树，最后遍历根结点。

// 后序遍历
void EndingepilogueOrder(BTNode* root)
{if (root == NULL){printf("N "); //打印空节点数据return;}EndingepiloguePrevOrder(root->left); //递归遍历左子树节点的数据EndingepiloguePrevOrder(root->right); //递归遍历右子树节点的数据printf("%d ", root->data); //输出节点数据
}

4. 层序遍历

层序遍历的做法和上述遍历做法不同，不能简单的调用递归来遍历，而是要借用到队列来辅助实现。队列的实现我就不在叙述了，层序遍历代码所示：

// 层序遍历
void BinaryTreeLevelOrder(BTNode* root)
{Quene q;QueneInit(&q);if (root){QuenePush(&q, root); //存入根节点}while (!QueneEmpty(&q)) //队列不为空就循环{BTNode* front = QueneFront(&q); //取出队列中的第一个节点QuenePop(&q); //删除第一个节点printf("%d ", front->data); //打印取出来第一个节点的数据if (front->left){QuenePush(&q, front->left); //如果左子树不为空，就将左子树存入队列}if (front->right){QuenePush(&q, front->right); //如果右子树不为空，就将右子树存入队列}}QueneDesTroy(&q);
}

🌲五、二叉树的计算

1. 计算二叉树结点个数

计算二叉树的结点个数，只需要将左子树的结点个数加上右子树的结点个数，最后再加上根结点就完成了。

int TreeSide(BTNode* root)
{return root == NULL ? 0 : TreeSide(root->left) + TreeSide(root->right) + 1; //运用条件表达式，如果根结点为空就返回0，否则就递归调用遍历左子树和右子树的结点个数，两者相加，最后再加一个最上面的根结点。
}

2. 计算二叉树叶子结点的个数

首先要明白什么是叶子结点，实际上就是度为0的结点即孩子结点。
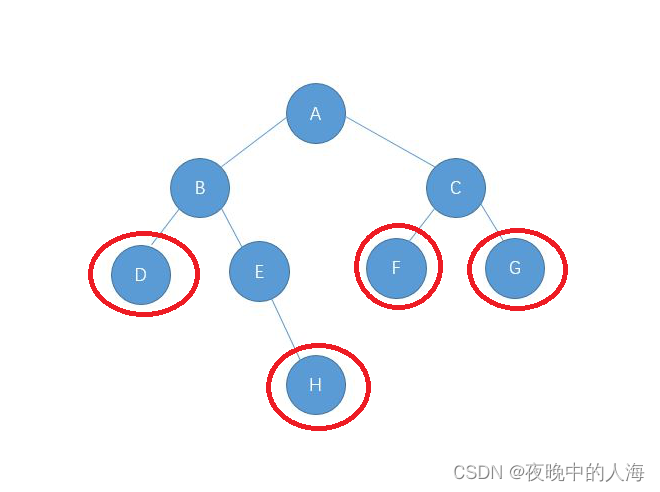
在这里插入图片描述
如上图，D、H、F、G都为叶子结点。代码展示：

int TreeLeafSize(BTNode* root)
{if (root == NULL){return 0; //空树返回0}else if (TreeLeafSize(root->left)== NULL && TreeLeafSize(root->right) == NULL){return 1; //只含有根节点就返回1}return TreeLeafSize(root->left) + TreeLeafSize(root->right); ///递归调用遍历左子树和右子树的叶子数，两者相加
}

3. 计算二叉树的深度

什么是二叉树的深度呢？简单的来说就是左子树或者右子树的深度+1。

// 求树的深度
int TreeHight(BTNode* root)
{if (root == NULL){return 0;}int highleft = TreeHight(root->left); //获取左子树的深度int highright = TreeHight(root->right); //获得右子树的深度return highleft > highright ? highleft + 1 : highright + 1; //运用条件表达式，返回左子树和右子树中较大的深度+1
}

4. 计算二叉树第k层的结点个数

实现这一操作的核心思路，就是要知道：求当前树的第k层结点个数 = 左子树的第k - 1层的结点个数 + 右子树的第k-1层的结点个数。

// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{if (root == NULL){return 0; // 空树返回0}if (k == 1){return 1; //第一层为根节点返回1}return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}

5. 查找二叉树中值为x的结点

这里需要注意的是，我们要记录查找到的结点，否则当我们想要返回所找到的结点数据，却发现又要重新递归去找，时间会消耗好几倍，因此需要记录找到的结点数据

BTNode* BinaryTreeFind(BTNode* root, BTDateType x)
{if (root == NULL){return NULL;}if (root->data == x){return root;}BTNode* left = BinaryTreeFind(root->left, x);if (left != NULL)return left;BTNode* right = BinaryTreeFind(root->right, x);if (right != NULL)return right;// 左右子树都没有return NULL;
}

6. 判断二叉树是否为完全二叉树

按照层序遍历的方式遍历完全二叉树，当我们遍历到空结点时，就开始判断。如果队列中还有空，就不是完全二叉树

// 判断二叉树是否为完全二叉树
bool BinaryTreeComplete(BTNode* root)
{Quene q;QueneInit(&q);if (root){QuenePush(&q, root);}while (!QueneEmpty(&q)){BTNode* front = QueneFront(&q);QuenePop(&q);// 遇到第一个空就开始判断，如果队列中还有空，就不是完全二叉树if (front == NULL){break;}QuenePush(&q, front->left);QuenePush(&q, front->right);}while (!QueneEmpty(&q)){BTNode* front = QueneFront(&q);QuenePop(&q);// 如果有非空，就不是完全二叉树if (front){QueneDesTroy(&q);return false;}}QueneDesTroy(&q);return true;
}

🏝️六、整体代码展示

#define _CRT_SECURE_NO_WARNINGS 1#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include "Quene.h"typedef int BTDateType;typedef struct BinaryTreeNode
{BTDateType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;// 手搓一个二叉树BTNode* BuyNode(int x)
{BTNode* node = (BTNode*)malloc(sizeof(BTNode));if (node == NULL){perror("malloc fail");return NULL;}node->data = x;node->left = NULL;node->right = NULL;
}BTNode* CreatBinaryTree()
{BTNode* node1 = BuyNode(1);BTNode* node2 = BuyNode(2);BTNode* node3 = BuyNode(3);BTNode* node4 = BuyNode(4);BTNode* node5 = BuyNode(5);BTNode* node6 = BuyNode(6);node1->left = node2;node1->right = node4;node2->left = node3;node4->left = node5;node4->right = node6;return node1;
}// 销毁
void BinaryTreeDestory(BTNode* root)
{if (root){BinaryTreeDestory(root->left);BinaryTreeDestory(root->right);free(root);root = NULL;}
}// 层序遍历
void BinaryTreeLevelOrder(BTNode* root)
{Quene q;QueneInit(&q);if (root){QuenePush(&q, root);}while (!QueneEmpty(&q)){BTNode* front = QueneFront(&q);QuenePop(&q);printf("%d ", front->data);if (front->left){QuenePush(&q, front->left);}if (front->right){QuenePush(&q, front->right);}}QueneDesTroy(&q);
}// 前序遍历
void PrevOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}printf("%d ", root->data);PrevOrder(root->left);PrevOrder(root->right);
}// 中序遍历
void InPrevOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}InPrevOrder(root->left);printf("%d ", root->data);InPrevOrder(root->right);
}// 后序遍历
void EndingepiloguePrevOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}EndingepiloguePrevOrder(root->left);EndingepiloguePrevOrder(root->right);printf("%d ", root->data);
}int TreeSide(BTNode* root)
{return root == NULL ? 0 : TreeSide(root->left) + TreeSide(root->right) + 1;
}// 求叶子结点的个数
int TreeLeafSize(BTNode* root)
{if (root == NULL){return 0;}else if (TreeLeafSize(root->left)== NULL && TreeLeafSize(root->right) == NULL){return 1;}return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}// 求树的深度
int TreeHight(BTNode* root)
{if (root == NULL){return 0;}int highleft = TreeHight(root->left);int highright = TreeHight(root->right);return highleft > highright ? highleft + 1 : highright + 1;
}// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{if (root == NULL){return 0;}if (k == 1){return 1;}return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDateType x)
{if (root == NULL){return NULL;}if (root->data == x){return root;}BTNode* left = BinaryTreeFind(root->left, x);if (left != NULL)return left;BTNode* right = BinaryTreeFind(root->right, x);if (right != NULL)return right;// 左右子树都没有return NULL;
}// 判断二叉树是否为完全二叉树
bool BinaryTreeComplete(BTNode* root)
{Quene q;QueneInit(&q);if (root){QuenePush(&q, root);}while (!QueneEmpty(&q)){BTNode* front = QueneFront(&q);QuenePop(&q);// 遇到第一个空就开始判断，如果队列中还有空，就不是完全二叉树if (front == NULL){break;}QuenePush(&q, front->left);QuenePush(&q, front->right);}while (!QueneEmpty(&q)){BTNode* front = QueneFront(&q);QuenePop(&q);// 如果有非空，就不是完全二叉树if (front){QueneDesTroy(&q);return false;}}QueneDesTroy(&q);return true;
}int main()
{BTNode* root = CreatBinaryTree();PrevOrder(root);printf("\n");InPrevOrder(root);printf("\n");EndingepiloguePrevOrder(root);printf("\n");printf("TreeSide:%d\n", TreeSide(root));printf("TreeLeafSize:%d\n", TreeLeafSize(root));printf("TreeHight:%d\n", TreeHight(root));printf("BinaryTreeFind:%p\n", BinaryTreeFind(root,3));printf("BinaryTreeLevelKSize:%d\n", BinaryTreeLevelKSize(root, 3));printf("\n");BinaryTreeLevelOrder(root);return 0;
}

今天的分享就到这里啦，如果感觉内容不错，记得一键三连噢。创作不易，感谢大家的支持，我们下次再见！ヾ(￣▽￣)ByeBye

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.rhkb.cn/news/332224.html

如若内容造成侵权/违法违规/事实不符，请联系长河编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

Go语言之GORM框架(二) ——GORM的单表操作

Go语言之GORM框架(二) ——GORM的单表操作

前言 在上一篇文章中&#xff0c;我们对Gorm进行了介绍&#xff0c;而在这一篇文章中我们主要介绍GORM的单表查询与Hook函数,在进行今天的内容之前我们先事先说明一下&#xff0c;下面我们对单表进行操作的表结构如下&#xff1a; type Student struct {ID uint gorm:&qu…
阅读更多...
C# WPF入门学习（四）—— 按钮控件

C# WPF入门学习（四）—— 按钮控件

上期介绍了WPF的实现架构和原理&#xff0c;之后我们开始来使用WPF来学习各种控件。 一、尝试插入一个按钮&#xff08;方法一&#xff09; 1. VS2019 在界面中&#xff0c;点击工具栏中的视图&#xff0c;在下拉菜单中选择工具箱。 至于编译器中的视图怎么舒服怎么来布置&am…
阅读更多...
肯尼亚大坝决堤反思：强化大坝安全监测的必要性

肯尼亚大坝决堤反思：强化大坝安全监测的必要性

一、背景介绍 近日&#xff0c;肯尼亚发生了一起严重的大坝决堤事件。当地时间4月29日&#xff0c;肯尼亚内罗毕以北的一座大坝决堤&#xff0c;冲毁房屋和车辆。当地官员称&#xff0c;事故遇难人数已升至71人。这起事件再次提醒我们&#xff0c;大坝安全无小事&#xff0c;监…
阅读更多...
绘唐3模型怎么放本地sd安装及模型放置位置 及云端sd部署

绘唐3模型怎么放本地sd安装及模型放置位置 及云端sd部署

绘唐3模型怎么放本地sd安装及模型放置位置 及云端sd部署 资料里面授权方式&#xff1a; https://qvfbz6lhqnd.feishu.cn/wiki/CcaewIWnSiAFgokOwLycwi0Encf 云端和模型之间存在某种关联性。云端通常用于存储和管理大量数据&#xff0c;并提供计算和资源的服务。模型是对数据进…
阅读更多...
揭秘 淘宝死店采集私信筛选，号称日赚500+

揭秘 淘宝死店采集私信筛选，号称日赚500+

淘宝死店采集工具为电子商务创业者揭示了一个领域的新机遇&#xff0c;通过提供一系列深入分析和资源挖掘的功能&#xff0c;展现了从失败中寻找成功之道的独特方法论。以下是如何通过这种工具寻找电商平台中的隐含机会的几个关键方面&#xff1a; 分析失败的深层原因&#x…
阅读更多...
简历–工作经历–通用

简历–工作经历–通用

雇主将会很注意简历中的工作经历这一部分。在看完求职目标后&#xff0c;他们想了解你的历史&#xff0c;你曾在哪儿工作&#xff0c;工作了多长时间。他们想弄明白的是“你是个稳定可靠的人吗&#xff1f;”&#xff0c;“你发挥出的才能有哪些&#xff1f;”最重要的是你是否…
阅读更多...
Java学习路线思维导图

Java学习路线思维导图

目录 Java学习流程1.学习大纲2.Java开发中常用的DOS命令 Java入门学习思维导图 Java学习流程 通过大纲了解学习的重点&#xff0c;通过目录依次深入【注&#xff1a;Java环境的搭建百度&#xff0c;提升自己百度的能力】 1.学习大纲 学习流程如下&#xff1a; Java基础语法 …
阅读更多...
vim操作手册

vim操作手册

vim分为插入模式、命令模式、底行模式。 插入模式&#xff1a;编辑模式 命令模式&#xff1a;允许使用者通过命令&#xff0c;来进行文本的编辑控制 底行模式&#xff1a;用来进行让vim进行包括但不限于shell进行交互 w&#xff1a;保存 wq&am…
阅读更多...
创新实训2024.05.26日志：服务端接口实现——用户开启多个会话

创新实训2024.05.26日志：服务端接口实现——用户开启多个会话

1. 概念图 类似于Kimi&#xff0c;文心一言&#xff0c;chatGPT等市面上主流的大模型&#xff0c;我们的大模型也支持同一个用户的多个会话&#xff0c;并且提供支持联系上下文给出解答的能力。 2. 基于会话的对话 在langchain chatchat这个对langchain框架进行二次封装的第三…
阅读更多...
属于程序员的浪漫，一颗会跳动的心！！！

属于程序员的浪漫，一颗会跳动的心！！！

绘制一颗会跳动的心❤ 嘿嘿 可以说是程序员的专属浪漫了吧&#xff0c;就像点燃一颗LED灯一样&#xff1f;&#xff08;我瞎说的啊&#xff0c;大家别当真&#xff0c;我很菜的&#xff01;&#xff01;&#xff01;&#xff01;&#xff09; 程序就在下面啦&#xff0c;然…
阅读更多...
2024HVV面经整理（一）2024HVV面经整理（一）

2024HVV面经整理（一）2024HVV面经整理（一）

阅读更多...
xgboost项目实战-保险赔偿额预测与信用卡评分预测001

xgboost项目实战-保险赔偿额预测与信用卡评分预测001

目录 算法代码 原理 算法流程 xgb.train中的参数介绍 params min_child_weight gamma 技巧 算法代码 代码获取方式&#xff1a;链接&#xff1a;https://pan.baidu.com/s/1QV7nMC5ds5wSh-M9kuiwew?pwdx48l 提取码&#xff1a;x48l 特征直方图统计&#xff1a; fig, …
阅读更多...
【Linux】进程通信实战 —— 进程池项目

【Linux】进程通信实战 —— 进程池项目

送给大家一句话: 没有一颗星&#xff0c;会因为追求梦想而受伤&#xff0c;当你真心渴望某样东西时&#xff0c;整个宇宙都会来帮忙。 – 保罗・戈埃罗 《牧羊少年奇幻之旅》 &#x1f3d5;️&#x1f3d5;️&#x1f3d5;️&#x1f3d5;️&#x1f3d5;️&#x1f3d5;️ &a…
阅读更多...
Stream流的使用

Stream流的使用

目录 一&#xff0c;Stream流 1.1 概述 1.2 Stream代码示例 二&#xff0c;Stream流的使用 2.1 数据准备 2.2 创建流对象 2.3 中间操作 filter map distinct sorted limit skip flatMap 2.4 终结操作 foreach count max&min collect 2.5 查找与匹配 a…
阅读更多...
免费图片文字转换成文本，ocr文字识别软件免费版，真的太实用了！

免费图片文字转换成文本，ocr文字识别软件免费版，真的太实用了！

截屏短视频上一段扎心文字&#xff0c;想把它发到朋友圈怎么办&#xff1f;这时候就需要一个OCR识别软件。 它就像一个聪明的小助手&#xff0c;它可以帮助电脑“看懂”书本上或者图片里的字。就像我们用眼睛看字一样&#xff0c;OCR软件用它的“眼睛”扫描图片&#xff0c;识…
阅读更多...
【组合数学】常考试题答案

【组合数学】常考试题答案

一、单项选择题&#xff08;每小题3分&#xff0c;共15分&#xff09; 1. 用3个“1”和4个“0”能组成&#xff08; &#xff09;个不同的二进制数字。 A. 35 B. 36, C. 37, D. 38 2. 整除300的正整数的个数为&#xff08; 　&#xff09;。 A. 14…
阅读更多...
Java进阶学习笔记27——StringBuilder、StringBuffer

Java进阶学习笔记27——StringBuilder、StringBuffer

StringBuilder&#xff1a; StringBuilder代表可变字符串对象&#xff0c;相当于一个容器&#xff0c;它里面装的字符串是可以改变的&#xff0c;就是用来操作字符串的。 好处&#xff1a; StringBuilder比String更适合做字符串的修改操作&#xff0c;效率会更高&#xff0c;…
阅读更多...
小白入职 必要熟悉 Git / tortoiseGit 工具

小白入职 必要熟悉 Git / tortoiseGit 工具

1.安装Git 1.1 了解Git Git是分布式版本控制系统&#xff0c;没有中央服务器的每个人的电脑就是一个完整的版本库&#xff0c;工作时无需联网可多人协作&#xff0c;只需把各自的修改推送给对方&#xff0c;就可以互相看到对方的修改了 分布式版本控制工具管理方式&#xff…
阅读更多...
AI崛起，掌握它，开启智能新生活！

AI崛起，掌握它，开启智能新生活！

AI崛起&#xff0c;掌握它&#xff0c;开启智能新生活&#xff01; &#x1f604;生命不息&#xff0c;写作不止 &#x1f525; 继续踏上学习之路&#xff0c;学之分享笔记 &#x1f44a; 总有一天我也能像各位大佬一样 &#x1f3c6; 博客首页 怒放吧德德 To记录领地 &…
阅读更多...
算法：树状数组

算法：树状数组

文章目录 面试题 10.10. 数字流的秩327. 区间和的个数315. 计算右侧小于当前元素的个数 树状数组可以理解一种数的存储格式。 面试题 10.10. 数字流的秩 假设你正在读取一串整数。每隔一段时间&#xff0c;你希望能找出数字 x 的秩(小于或等于 x 的值的个数)。 请实现数据结构…
阅读更多...
最新文章
推荐文章

Copyright @ 2022~2023