这是我的第287篇原创文章。
一、引言
主成分分析(Principal Component Analysis, PCA)是一种常用的降维技术,它通过线性变换将原始特征转换为一组线性不相关的新特征,称为主成分,以便更好地表达数据的方差。
在特征重要性分析中,PCA 可以用于理解数据中最能解释方差的特征,并帮助识别对目标变量影响最大的特征。可以通过查看PCA的主成分(主特征向量)以及各主成分所对应的特征重要性来推断哪些原始特征在新特征中起到了较大影响。
PCA 的局限性:
- PCA 是一种线性变换方法,可能无法很好地处理非线性关系的数据。
- PCA 可能会丢失一些信息,因为它主要关注的是数据中的方差,而忽略了其他方面的信
- PCA 假设主成分与原始特征之间是线性关系,这在某些情况下可能不成立。
二、实现过程
2.1 读取数据
# 准备数据
data = pd.read_csv(r'dataset.csv')
df = pd.DataFrame(data)
print(df)
# 目标变量和特征变量
target = 'target'
features = df.columns.drop(target)
# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(df[features], df[target], test_size=0.2, random_state=0)df:

2.2 对训练集做PCA主成分分析
自主选择主成分,并打印出每个主成分的解释性方差:
pca = PCA(n_components='mle')
pca.fit(X_train)
var_ratio = pca.explained_variance_ratio_
for idx, val in enumerate(var_ratio, 1):print("Principle component %d: %.2f%%" % (idx, val * 100))
print("total: %.2f%%" % np.sum(var_ratio * 100))结果:
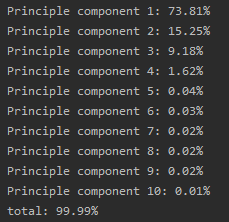
共计10个主成分。
2.3 通过主成分分析原始特征重要性
打印出每个特征对于主成分的系数,这反映了原始特征的重要性:
print(pca.components_)结果:
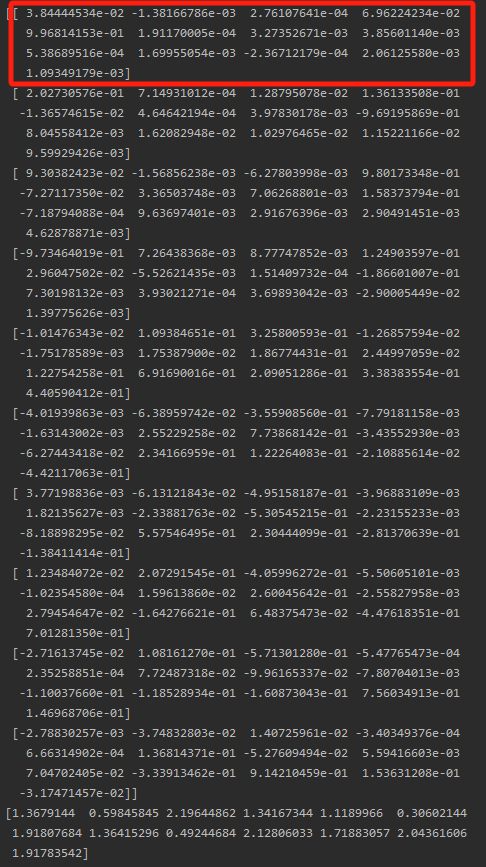
通过计算10个主成分中,每个原始特征的系数绝对值之和作为该特征的最终贡献度:
# 计算原始特征与主成分的相关性(绝对值)
feature_importance = np.abs(pca.components_)
# 计算每个主成分中原始特征的权重(系数)和
feature_importance_sum = np.sum(feature_importance, axis=0)
# 打印原始特征的重要性(贡献度)
print("\n原始特征的重要性(贡献度):")
ranking_df = pd.DataFrame({'特征': features, '贡献度': feature_importance_sum})
ranking_df = ranking_df.sort_values(by='贡献度')
print(ranking_df)结果:
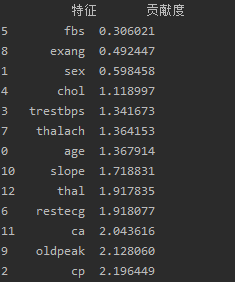
可视化:
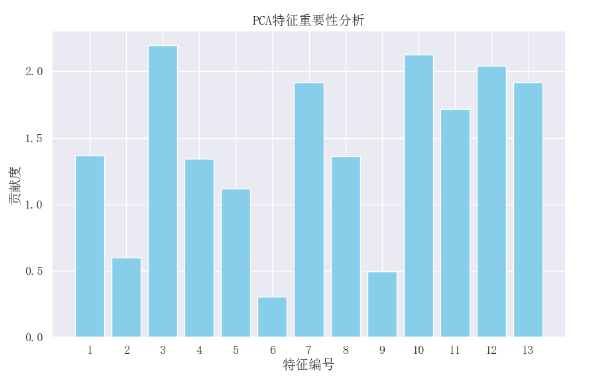
2.4 查看累计解释方差比率与主成分个数的关系
fig, ax = plt.subplots(figsize=(10, 7))
ax.plot(np.arange(1, len(var_ratio) + 1), np.cumsum(var_ratio), "-ro")
ax.set_title("Cumulative Explained Variance Ratio", fontsize=15)
ax.set_xlabel("number of components")
ax.set_ylabel("explained variance ratio(%)")
plt.show()结果:
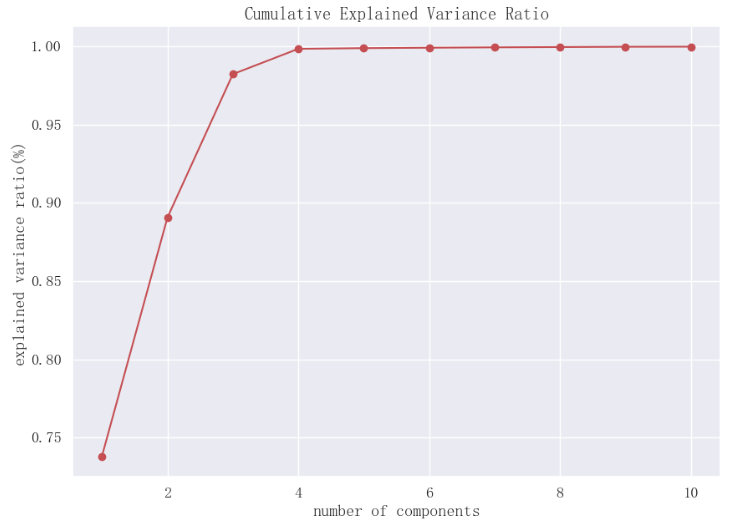
前2个主成分累计解释性方差比率接近0.9,前3个主成分累计解释方差比率超过0.95。
2.5 自动选择最优的主成分个数
设定累计解释方差比率的目标,让sklearn自动选择最优的主成分个数:
target = 0.9 # 保留原始数据集90%的变异
res = PCA(n_components=target).fit_transform(X_train)
print("original shape: ", X_train.shape)
print("transformed shape: ", res.shape)结果:
![]()
选择了3个主成分。
2.6 主成分选择可视化(以2个主成分为例)
选择两个主成分,并进行可视化:
pca=PCA(n_components=2) #加载PCA算法,设置降维后主成分数目为2
reduced_x=pca.fit_transform(X_train)#对样本进行降维
principalDf = pd.DataFrame(data = reduced_x, columns = ['principal component 1', 'principal component 2'])
print(principalDf)
y_train = np.array(y_train)
yes_x,yes_y=[],[]
no_x,no_y=[],[]
for i in range(len(reduced_x)):if y_train[i] ==1:yes_x.append(reduced_x[i][0])yes_y.append(reduced_x[i][1])elif y_train[i]==0:no_x.append(reduced_x[i][0])no_y.append(reduced_x[i][1])
plt.scatter(yes_x,yes_y,c='r',marker='x')
plt.scatter(no_x,no_y,c='b',marker='D')
plt.xlabel("First Main Component")
plt.ylabel("Second Main Component")
plt.show()结果:
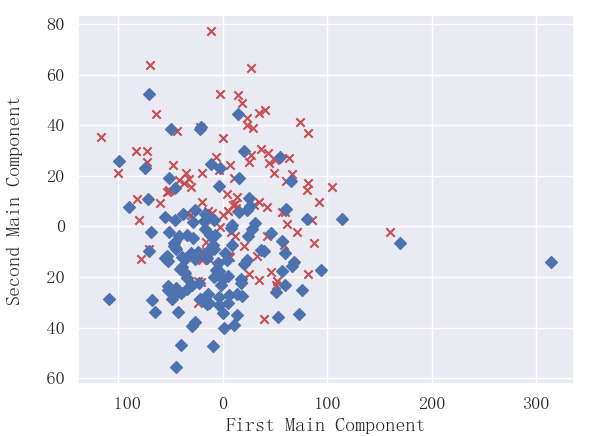
可以看出2个主成分可以大概划分出两类。
作者简介:
读研期间发表6篇SCI数据挖掘相关论文,现在某研究院从事数据算法相关科研工作,结合自身科研实践经历不定期分享关于Python、机器学习、深度学习、人工智能系列基础知识与应用案例。致力于只做原创,以最简单的方式理解和学习,关注我一起交流成长。需要数据集和源码的小伙伴可以关注底部公众号添加作者微信。