leetcode437 路径总和III-哈希表+前缀和

题目

给定一个二叉树的根节点 root ，和一个整数 targetSum ，求该二叉树里节点值之和等于 targetSum 的路径的数目。

路径不需要从根节点开始，也不需要在叶子节点结束，但是路径方向必须是向下的（只能从父节点到子节点）。

示例

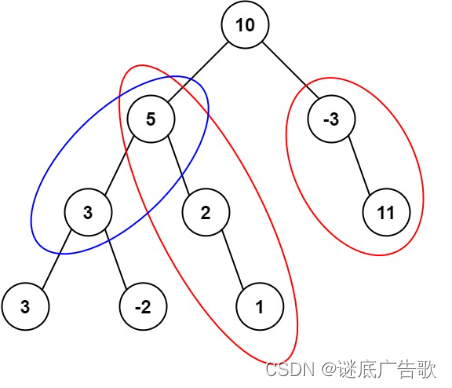
输入：root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8
输出：3
解释：和等于 8 的路径有 3 条，如图所示。
在这里插入图片描述

解析

这道题单单使用dfs的方法的话，基本上还是可以想到思路的：

/*** Definition for a binary tree node.* type TreeNode struct {*     Val int*     Left *TreeNode*     Right *TreeNode* }*/
func pathSum(root *TreeNode, targetSum int) int {if root == nil {return 0}res := rootSum(root, targetSum)res += pathSum(root.Left, targetSum)res += pathSum(root.Right, targetSum)return res
}func rootSum(root *TreeNode, targetSum int) int {res := 0if root == nil {return res}if root.Val == targetSum {res++}res += rootSum(root.Left, targetSum-root.Val)res += rootSum(root.Right, targetSum-root.Val)return res
}

然后实际上，这道题最好的解法是哈希表+前缀和的思路：
在二叉树上，前缀和相当于从根节点开始的路径元素和。用哈希表 cnt 统计前缀和的出现次数，当我们递归到节点 node时，设从根到 node 的路径元素和为 s，那么就找到了 cnt[s−targetSum]个符合要求的路径，加入答案。
在其中的恢复现场部分：如果不恢复现场，当我们递归完左子树，要递归右子树时，cnt中还保存着左子树的数据。但递归到右子树，要计算的路径并不涉及到左子树的任何节点，如果不恢复现场，cnt中统计的前缀和个数会更多，我们算出来的答案可能比正确答案更大。

func pathSum(root *TreeNode, targetSum int) (ans int) {cnt := map[int]int{0: 1} // 01是防止包含根节点的时候找不到var dfs func(*TreeNode, int)dfs = func(node *TreeNode, s int) {if node == nil {return}// 判断是否存在符合条件的前缀和s += node.Valans += cnt[s-targetSum]// 将当前前缀和记录下来cnt[s]++// 继续向下递归dfs(node.Left, s)dfs(node.Right, s)// 回溯，恢复状态cnt[s]--return}dfs(root, 0)return
}