VGG论文解析—Very Deep Convolutional Networks for Large-Scale Image Recognition -2015
研究背景
大规模图像识别的深度卷积神经网络 VGG(牛津大学视觉几何组)
认识数据集:ImageNet的大规模图像识别挑战赛
LSVRC-2014:ImageNet Large Scale Visual Recoanition Challenge(14年的相关比赛)
相关研究借鉴:
AlexNet ZFNet OverFeat
研究成果
-
ILSVRC定位冠军,分类亚军
-
开源VGG16,VGG19
-
开启小卷积核,深度卷积模型时代3*3卷积核成为主流模型
LSVRC: ImageNet Large Scale Visual Recognition Challenge 是李飞飞等人于2010年创办的图像识别挑战赛,自2010起连续举办8年,极大地推动计算机视觉发展。
比赛项目涵盖:图像分类(Classification)、目标定位(Object localization)、目标检测(Object detection)、视频目标检测(Object detection from video)、场景分类(Scene classification)、场景解析(Scene parsing)
竞赛中脱颖而出大量经典模型:
alexnet,vgg,googlenet ,resnet,densenet等
- AlexNet:ILSVRC-2012分类冠军,里程碑的CNN模型
- ZFNet:ILSVRC-2013分类冠军方法,对AlexNet改进
- OverFeat:ILSVRC-2013定位冠军,集分类、定位和检测于一体的卷积网络方法(即将全连接层替换为1x1的卷积层)
论文精读
摘要
In this work we investigate the effect of the convolutional network depth on its accuracy in the large-scale image recognition setting. Our main contribution is a thorough evaluation of networks of increasing depth using an architecture with very small (3×3) convolution filters, which shows that a significant improvement on the prior-art configurations can be achieved by pushing the depth to 16–19 weight layers. These findings were the basis of our ImageNet Challenge 2014 submission, where our team secured the first and the second places in the localisation and classification tracks respectively. We also show that our representations
generalise well to other datasets, where they achieve state-of-the-art results. We have made our two best-performing ConvNet models publicly available to facilitate further research on the use of deep visual representations in computer vision.
摘要进行解读
- 本文主题:在大规模图像识别任务中,探究卷积网络深度对分类准确率的影响
- 主要工作:研究3*3卷积核增加网络模型深度的卷积网络的识别性能,同时将模型加深到16-19层
- 本文成绩:VGG在ILSVRC-2014获得了定位任务冠军和分类任务亚军
- 泛化能力:VGG不仅在ILSVRC获得好成绩,在别的数据集中表现依旧优异
- 开源贡献:开源两个最优模型,以加速计算机视觉中深度特征表示的进一步研究
快速泛读论文确定小标题的结构
- Introduction
- ConvNet Configurations
- 2.1 Architecture
- 2.2 Configuratoins
- 2.3 Discussion
- Classification Framework
- 3.1 Training
- 3.2Testing
- 3.3ImplementationDetails
- Classification Experiments
- 4.1 Singlescaleevaluation
- 4.2 Multi-Scale evaluation
- 4.3 Multi-Cropevaluation
- 4.4 ConvNetFusion
- 4.5 Comparison with the state of the art
- Conclusion
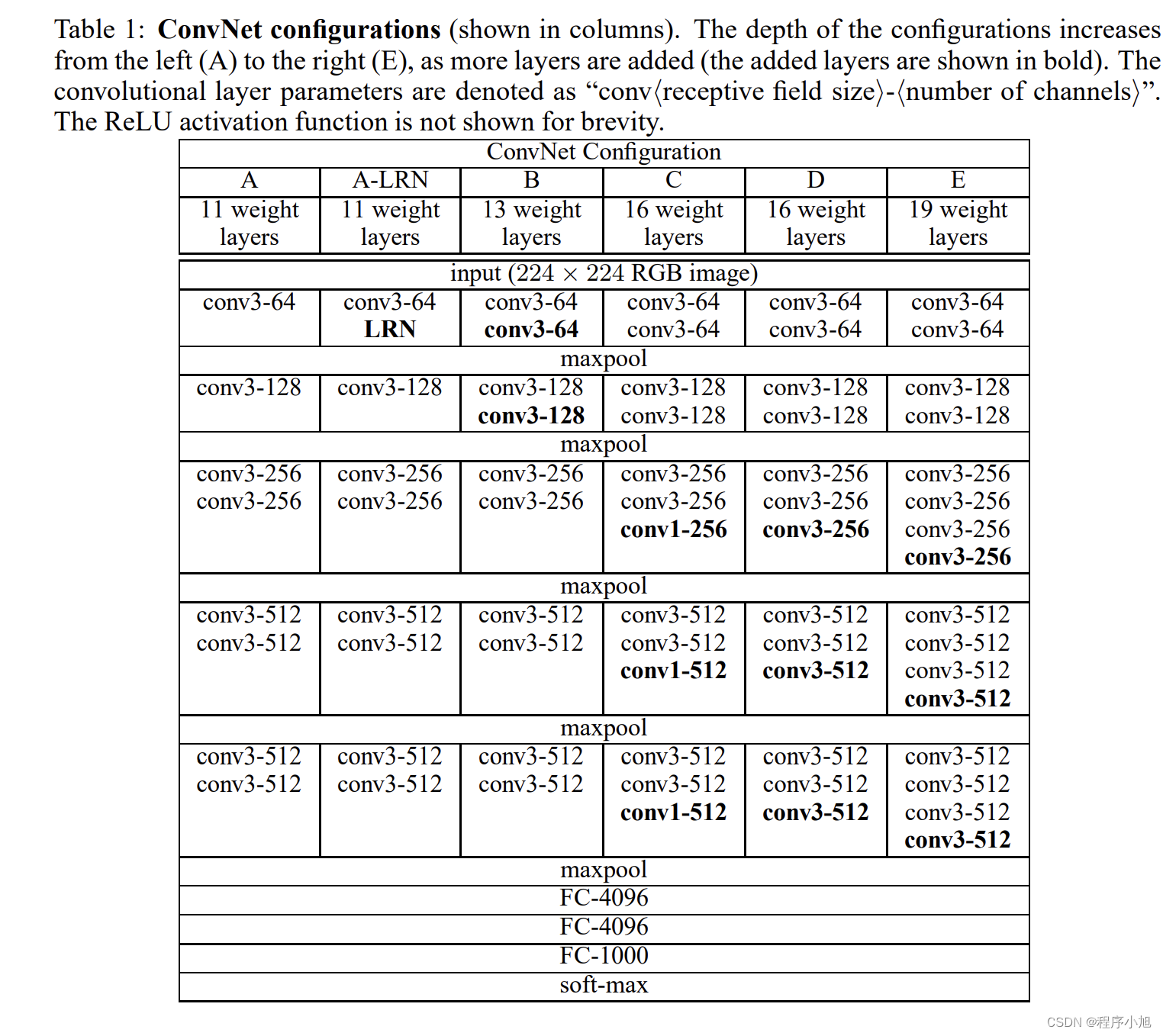
根据图表结构:论文中提出了A A-LRN B C D E等五种VGG网络对应的论文结构。
VGG网络结构
模型结构
During training, the input to our ConvNets is a fixed-size 224 × 224 RGB image. The only preprocessing we do is subtracting the mean RGB value, computed on the training set, from each pixel.
The image is passed through a stack of convolutional (conv.) layers, where we use filters with a very small receptive field: 3 × 3 (which is the smallest size to capture the notion of left/right, up/down,center). In one of the configurations we also utilise 1 × 1 convolution filters, which can be seen as a linear transformation of the input channels (followed by non-linearity). The convolution stride is fixed to 1 pixel; the spatial padding of conv. layer input is such that the spatial resolution is preserved after convolution, i.e. the padding is 1 pixel for 3 × 3 conv. layers. Spatial pooling is carried out by five max-pooling layers, which follow some of the conv. layers (not all the conv. layers are followed by max-pooling). Max-pooling is performed over a 2 × 2 pixel window, with stride 2.
A stack of convolutional layers (which has a different depth in different architectures) is followed by three Fully-Connected (FC) layers: the first two have 4096 channels each, the third performs 1000- way ILSVRC classification and thus contains 1000 channels (one for each class). The final layer is the soft-max layer. The configuration of the fully connected layers is the same in all networks. All hidden layers are equipped with the rectification (ReLU (Krizhevsky et al., 2012)) non-linearity. We note that none of our networks (except for one) contain Local Response Normalisation (LRN) normalisation (Krizhevsky et al., 2012): as will be shown in Sect. 4, such normalisation does not improve the performance on the ILSVRC dataset, but leads to increased memory consumption and computation time. Where applicable, the parameters for the LRN layer are those of (Krizhevsky et al., 2012).
论文的原文中提到了整个VGG网络的输入是224 x 224的RGB三通道的彩色图片。使用了大小为3x3的卷积核(也尝试的使用了1x1的卷积核)同时使用了2x2的最大池化,步长为2同时不在使用LRN这种方法
11 weight layers in the network A(8 conv. and 3 FC layers) to 19 weight layers in the network E (16 conv. and 3 FC layers).
VGG11由8个卷积层和3个全连接层组成,VGG19由16个卷积层和3个全连接层组成
整个全连接层与AlexNet相同都是4096 x 4096 x1000,最后通过softmax函数完成1000分类、
整个VGG全部采用3x3的卷积
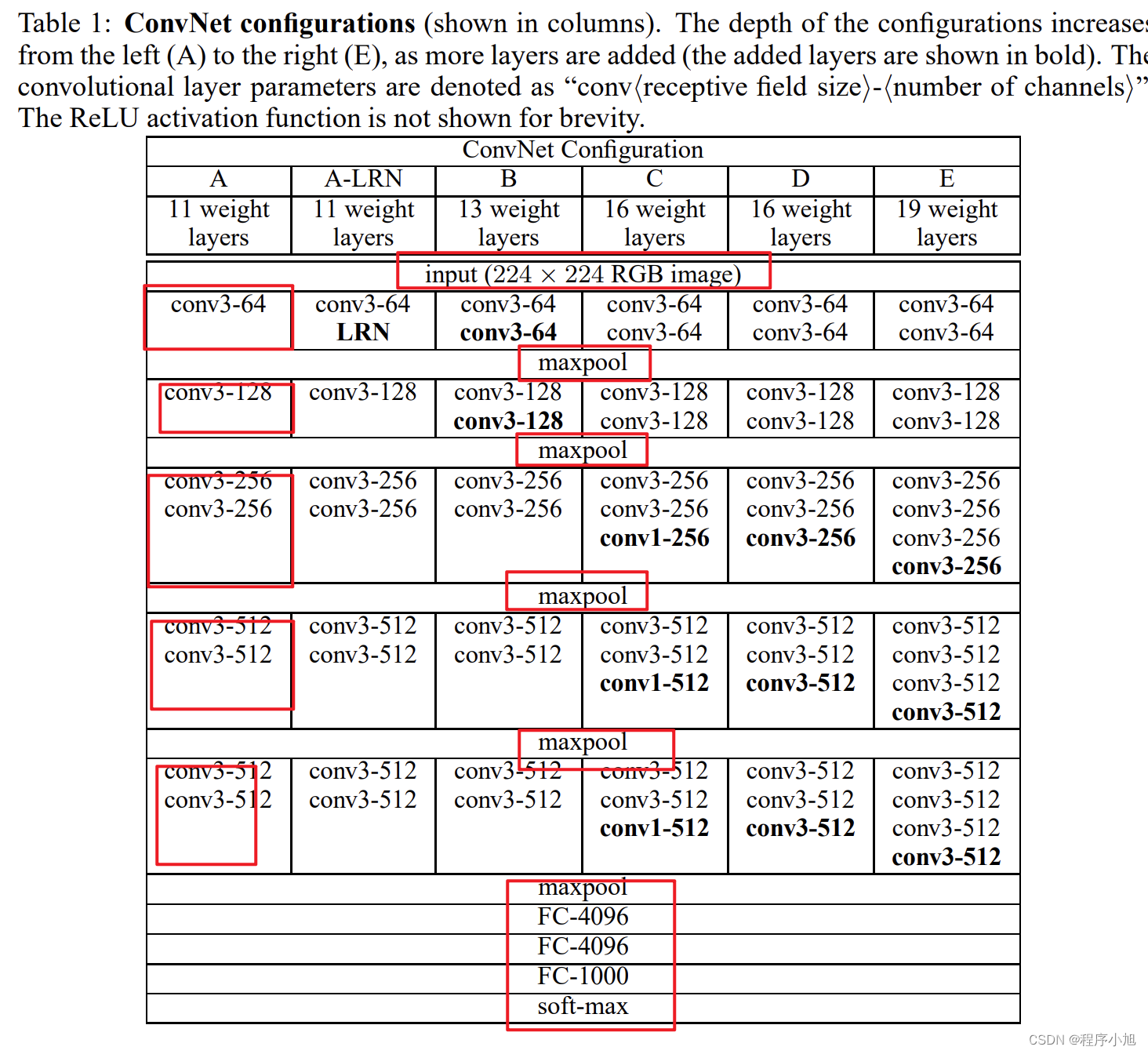
对A(VGG11)的过程和共性进行解读
首先论文中使用的是:224x224x3的一个输入,我们设置的是3x3的卷积核,论文中的作者进行了padding填充(1)保持经过卷积之后的图片大小不变。(conv-64)因此经过了第一层的卷积之后,得到了224x224x64的输出。
而最大池化的步骤2x2且步长为2
F o = ⌊ F in − k + 2 p s ⌋ + 1 F_{o}=\left\lfloor\frac{F_{\text {in }}-k+2 p}{s}\right\rfloor+1 Fo=⌊sFin −k+2p⌋+1
按照公式进行计算:
(224-2)/2 +1=112 因此输出是112x112的大小,在512之前,每次的通道数翻倍。
卷积不改变图片的大小,池化使得图片的大小减半,通道数翻倍
共性
- 5个maxpool
- maxpool后,特征图通道数翻倍直至512
- 3个FC层进行分类输出
- maxpool之间采用多个卷积层堆叠,对特征进行提取和抽象
参数计算

说明了网络的层数变化,对参数的变化影响不大

F i × ( K s × K s ) × K n + K n F_{i} \times\left(K_{\mathrm{s}} \times K_{\mathrm{s}}\right) \times K_{n}+K_{n} Fi×(Ks×Ks)×Kn+Kn
模型演变
A:11层卷积(VGG11)
A-LRN:基于A增加一个LRN
B:第1,2个block中增加1个卷积33卷积
C:第3,4,5个block分别增加1个11卷积
表明增加非线性有益于指标提升
D:第3,4,5个block的11卷积替换为33(VGG16)
E:第3,4,5个block再分别增加1个3*3卷积
其中最为常用的结构就是A中的VGG11和D中的VGG16
VGG的特点
- 堆叠3x3的卷积核
增大感受野2个33堆叠等价于1个553个33堆叠等价于1个77
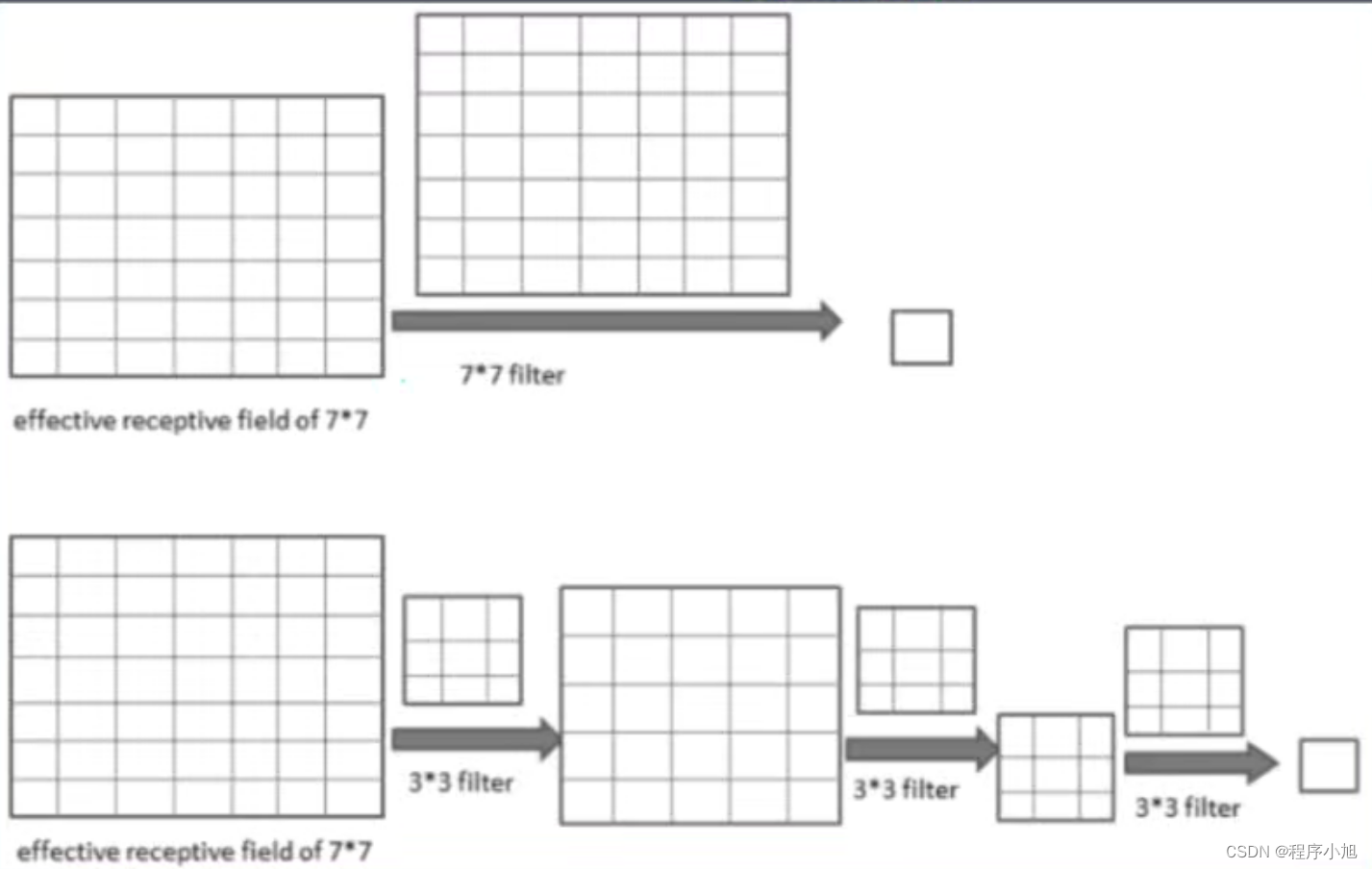
增加非线性激活函数,增加特征抽象能力
减少训练参数
可看成7 * 7卷积核的正则化,强迫7 * 7分解为3 * 3
假设输入,输出通道均为C个通道
一个77卷积核所需参数量:7 * 7 C * C=49C2
三个33卷积核所需参数量:3(3 * 3* C *C)=27C2
参数减少比:(49-27)/49~44%
之后的数据处理过程和测试过程的相关的内容,放到之后在进行下一次的解读,通过这一次主要要理解的是VGG的网络结构