前言

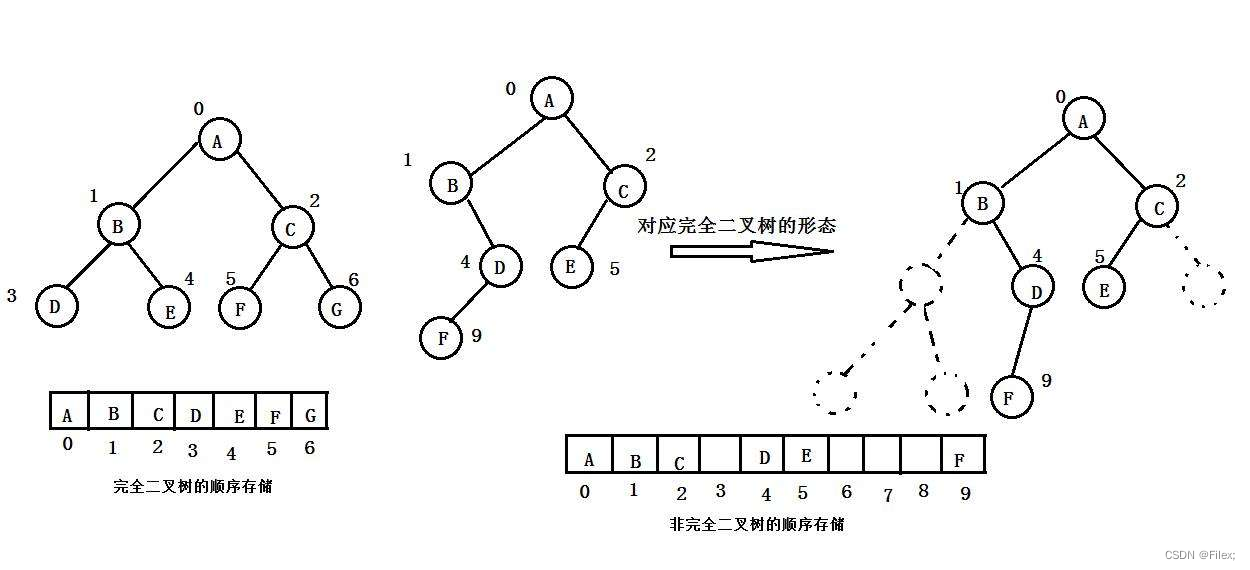
普通的二叉树是不适合用数组来存储的，因为可能会存在大量的空间浪费。而完全二叉树更适合使用顺序结
构存储。现实中我们通常把堆(一种二叉树)使用顺序结构的数组来存储，需要注意的是这里的堆和操作系统
虚拟进程地址空间中的堆是两回事，一个是数据结构，一个是操作系统中管理内存的一块区域分段。

一、堆的概念及结构

⼆叉堆本质上是⼀种 完全⼆叉树，它分为两个类型，最大堆 和 最小堆。

堆的性质：

1)堆中某个结点的值总是不大于或不小于其父结点的值；
2)堆总是一棵完全二叉树。

堆的结构:

最大堆

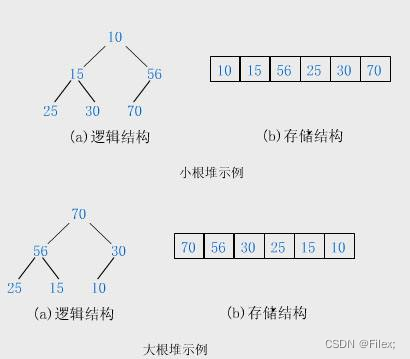
最⼤堆的任何⼀个⽗节点的值，都 ⼤于 或 等于 它左、右孩⼦节点的值（如下图所示）。

最小堆

最⼩堆的任何⼀个⽗节点的值，都 ⼩于 或 等于 它左、右孩⼦节点的值（如下图所示）。

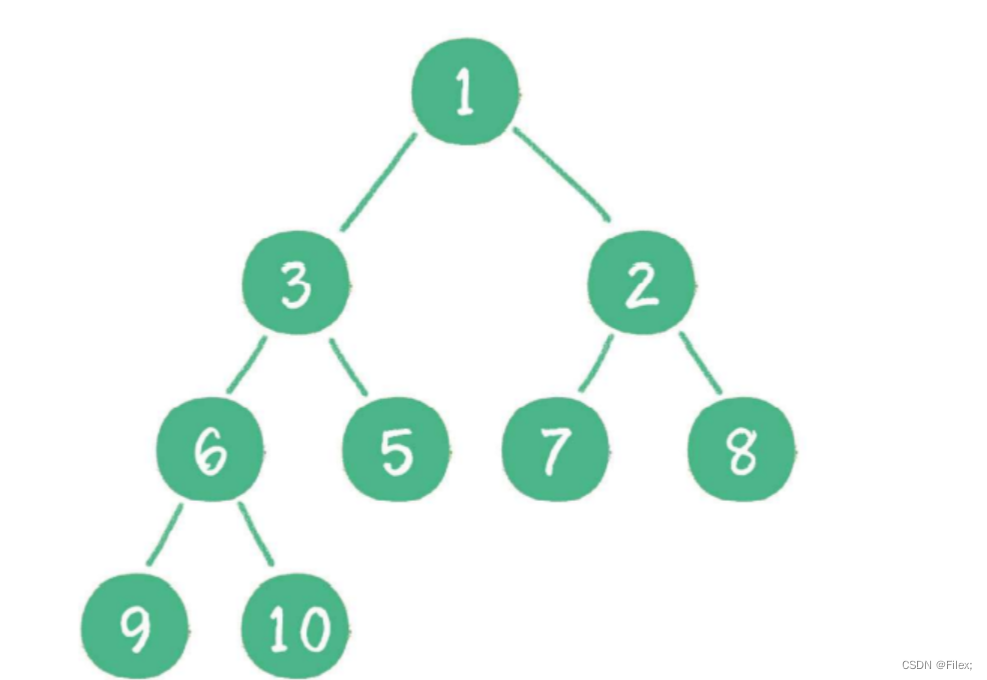
堆顶

⼆叉堆的根节点叫作 堆顶 。

最⼤堆和最⼩堆的特点决定了：

1）最⼤堆的堆顶是整个堆中的 最⼤元素；
2）最⼩堆的堆顶是整个堆中的 最⼩元素 。

注意

在实现堆的代码之前，我们还需要明确⼀点：⼆叉堆虽然是⼀个完全⼆叉树，但它的存储⽅式并不是链式存储，⽽是 顺序存储。

换句话说，⼆叉堆的所有节点都存储在数组中（如下图所示）。

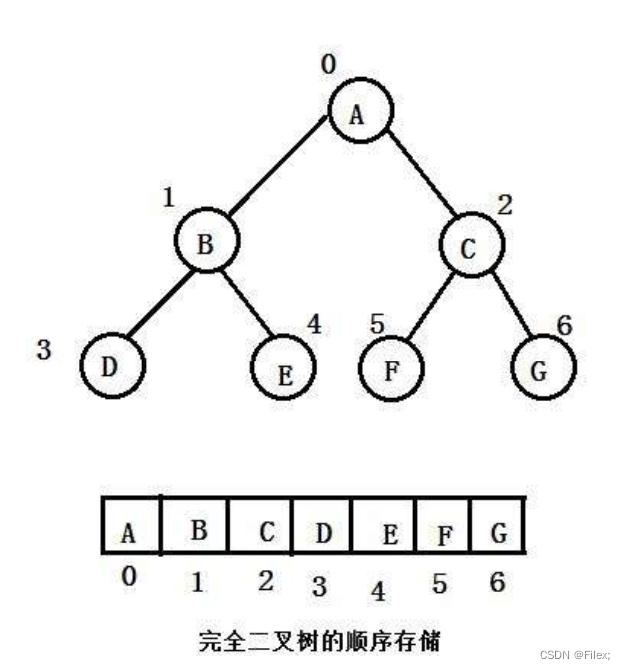
在数组中，在没有左、右指针的情况下，如何定位⼀个⽗节点的左孩⼦和右孩⼦呢？

我们可以通过数组下标来计算。

假 设 ⽗ 节 点 的 下 标 是 parent 。
那 么 它 的 左 孩 ⼦ 下 标 就 是 2 × p a r e n t + 1 ；
右 孩 ⼦ 下 标 就 是 2 × p a r e n t + 2 。

二、堆的实现

1.初始化堆

首先，创建一个堆的类型，该类型中需包含堆的基本信息：存储数据的数组、堆中元素的个数 以及 当前堆的最大容量。

typedef int HPDataType;typedef struct Heap
{HPDataType* a;int size;int capacity;
}HP;

然后我们需要一个初始化函数，对刚创建的堆进行初始化。

void HPInit(HP* php)
{assert(php);php->a = NULL;php->capacity = php->size = 0;
}

2. 堆的插入

当⼆叉堆插⼊节点时，插⼊位置是完全⼆叉树的最后⼀个位置。

例如插⼊⼀个新节点，值是10（如下图所示）。

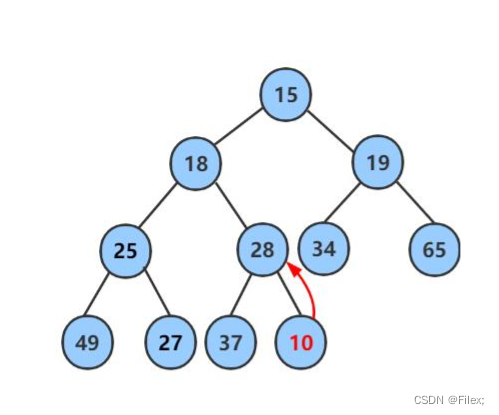
这时，新节点的⽗节点 28 ⽐ 10 ⼤，显然不符合 最⼩堆 的性质。于是让新节点 “上浮”，和⽗节点交换位置（如下图所示）。

继续⽤节点 10 和⽗节点 18 做⽐较，因为 10 ⼩于 18，则让新节点继续 “上浮”（如下图所示）。

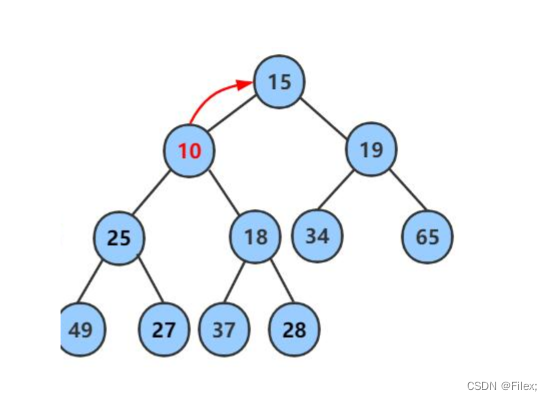
继续⽐较，最终新节点 10 “上浮” 到了堆顶位置（如下图所示）。

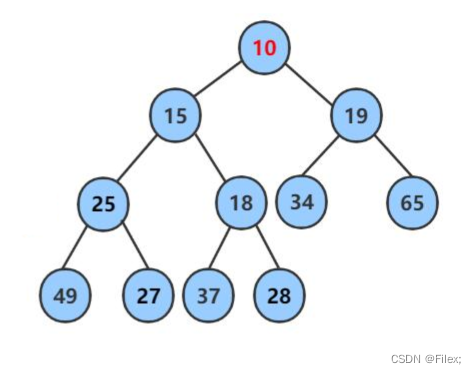
这种方法叫做 堆的向上调整算法。

什么是堆的向上调整算法？

在对二叉堆进行 插入数据 时，要使用 向上调整算法，它既可以构建 大堆，也可以构建 小堆。

核心思路（以构建小堆为例）：

1）将目标节点与其父节点比较。
2）若目标节点的值比其父节点的值小，则交换目标节点与其父节点的位置，并将原目标节点的父结点当作新的目标节点继续进行向上调整。
3）若目标节点的值比其父节点的值大，则停止向上调整，此时该完全二叉树已经是小堆了。

代码示例：

交换变量
void Swap(HPDataType* p1, HPDataType* p2)
{HPDataType tmp = 0;tmp = *p1;*p1 = *p2;*p2 = tmp;
}void AdjustUp(HPDataType* a, int child)
{//建小堆int parent = (child - 1) / 2;while (child > 0) 调整到根节点的位置截止{if (a[child] < a[parent]) 如果孩子节点的值小于父节点的值{Swap(&a[child], &a[parent]); 将父结点与孩子节点交换child = parent; 继续向上进行调整parent = (child - 1) / 2;}else{break; 已经是小堆了，直接跳出循环}}}

ps: 向上调整构建大堆

其实构建大堆只是把上面构建小堆中 if 语句中的 小于 改成了 大于。

既然 堆的插入 是向上调整，那我们直接用刚刚写好的函数就好了，这里以构建 小堆 为例。

代码示例：

void HPPush(HP* php, HPDataType x)
{assert(php);if (php->a == NULL){//扩容int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;HP* tmp = (HP*)realloc(php->a, sizeof(HPDataType) * newcapacity);if (tmp == NULL){perror("realloc tail");exit(1);}php->a = tmp;php->capacity = newcapacity;}php->a[php->size++] = x;AdjustUp(php->a, php->size - 1);}

3.堆的删除

⼆叉堆删除节点的过程和插⼊节点的过程正好相反，所删除的是处于堆顶的节点。

例如删除 最⼩堆 的堆顶节点 1（如下图所示）。

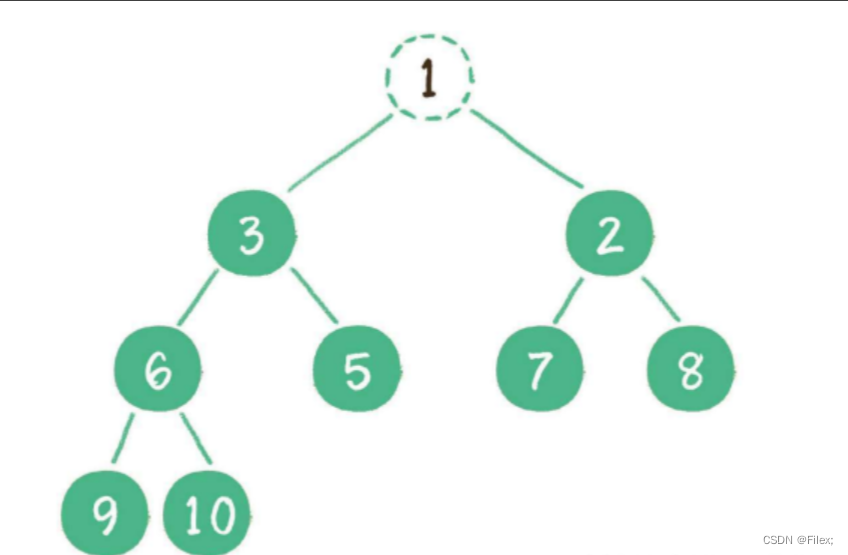
这时，为了继续维持完全⼆叉树的结构，我们把堆的最后⼀个节点 10 临时补到原本堆顶的位置（如下图所示）。

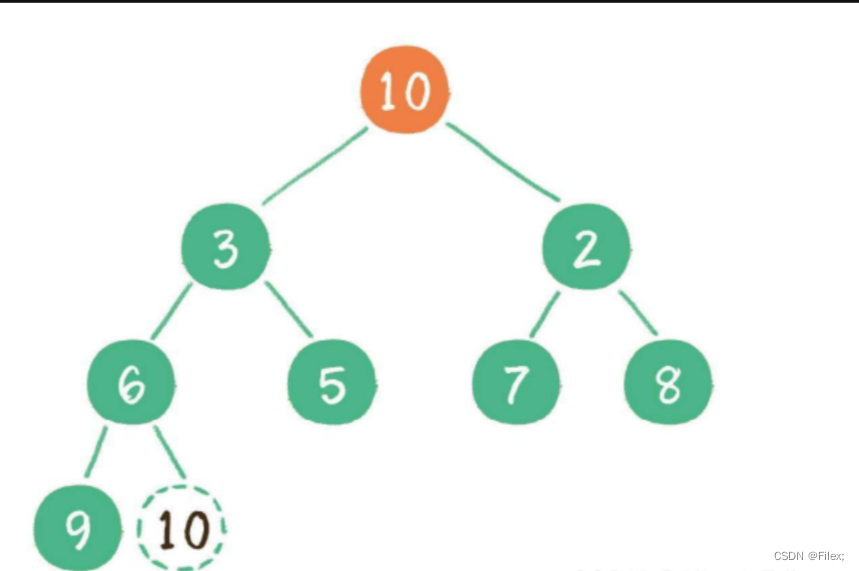
接下来，让暂处堆顶位置的节点 10 和它的左、右孩⼦进⾏⽐较，如果左、右孩⼦节点中最⼩的⼀个（显然是节点 2 ）⽐节点 10 ⼩，那么让节点 10 “下沉”（如下图所示）。

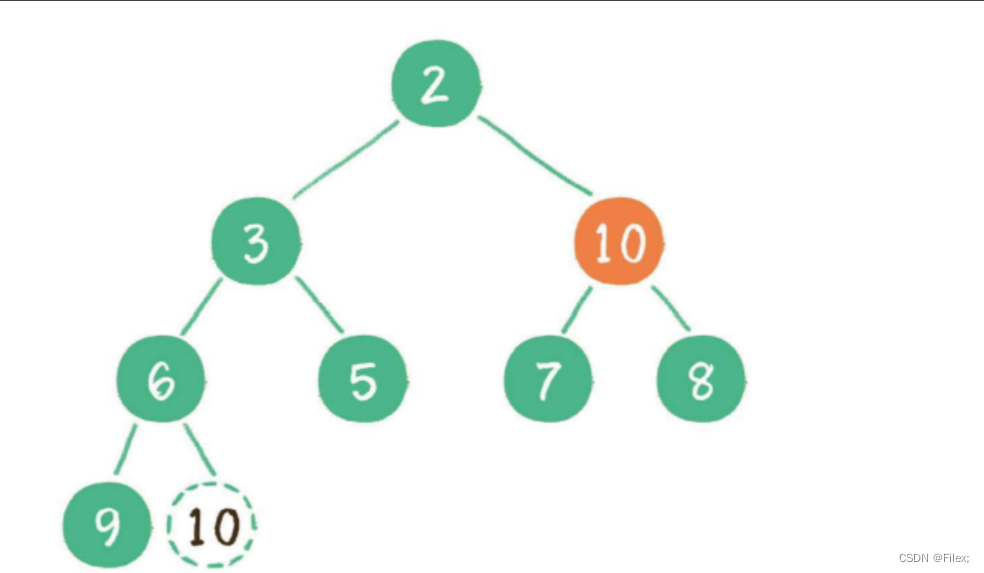
继续让节点 10 和它的左、右孩⼦做⽐较，左、右孩⼦中最⼩的是节点 7，由于 10 ⼤于 7，让节点 10 继续 “下沉”（如下图所示）。

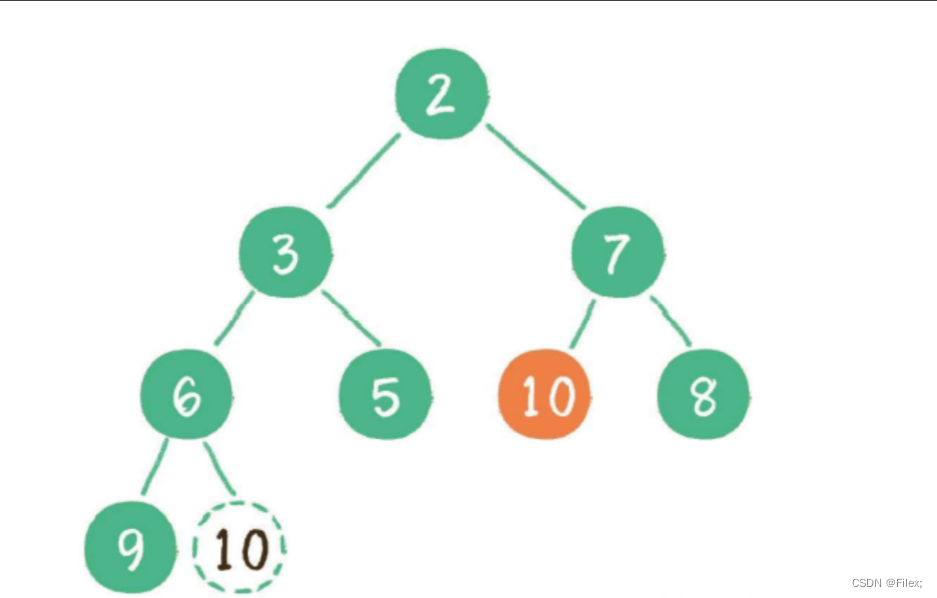
这种方法叫 堆的向下调整算法。

什么是堆的向下调整算法？

首先若想将其调整为小堆，那么根结点的左右子树必须都为小堆。

若想将其调整为大堆，那么根结点的左右子树必须都为大堆。

也就是说：

如果我们使用 向上调整算法 构建了一个 小堆，那么 向下调整算法 也必须只能调整 小堆。
如果我们使用 向上调整算法 构建了一个 大堆，那么 向下调整算法 也必须只能调整 大堆。

核心思路（以调整小堆为例）：

1）从根结点处开始，选出左右孩子中值较小的孩子。
2）让小的孩子与其父亲进行比较。
3）若小的孩子比父亲还小，则该孩子与其父亲的位置进行交换。并将原来小的孩子的位置当成父亲继续向下进行调整，直到调整到叶子结点为止。
4）若小的孩子比父亲大，则不需处理了，调整完成，整个树已经是小堆了。

代码示例:

交换变量
void Swap(HPDataType* p1, HPDataType* p2)
{HPDataType tmp = 0;tmp = *p1;*p1 = *p2;*p2 = tmp;
}void AdjustDown(HPDataType* a, int n, int parent)
{//建小堆假设左孩子小int child = parent * 2 + 1;while(child < n){在孩子存在的前提下，如果右孩子比【默认的左孩子】还要小，那么就把 child 指向右孩子；如果右孩子比左孩子大，那么就不进入if语句if ((child + 1) < n && a[child + 1] < a[child]){child++;}如果孩子小于父亲，则交换，并继续往下调整if (a[child] < a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}}

既然 堆的删除 是 向下调整，那我们直接用刚刚写好的函数就好了。
上面的 插入 是构建的小堆，所以这里删除调整的应该也必须是 小堆 。

void HPPop(HP* php)
{assert(php);Swap(&php->a[0], &php->a[php->size - 1]); 把堆顶的数据和最后一个位置的数据互换php->size--; 删除最后一个节点（也就是删除原来堆顶的元素）AdjustDown(php->a, php->size, 0); 向下调整（调小堆）
}

4.获取堆顶的数据

获取堆顶的数据，即返回数组下标为 0 的数据。

代码示例:

// 取堆顶的数据
HPDataType HeapTop(HP* php) {assert(php);assert(php->size > 0);return php->a[0]; //返回堆顶数据
}

5.获取堆的数据个数

获取堆的数据个数，即返回堆结构体中的 size 变量。

代码示例:

// 堆的数据个数
int HeapSize(HP* php) {assert(php);return php->size; //返回堆中数据个数
}

6.堆的判空

堆的判空，即判断堆结构体中的 size 变量是否为 0。

代码示例:

// 堆的判空
bool HeapEmpty(HP* php) {assert(php);//如果size等于0就为空，不等于0就不为空return php->size == 0;
}

7.堆的销毁

为了避免内存泄漏，使用完动态开辟的内存空间后都要及时释放该空间。

代码示例:

// 堆的销毁
void HeapDestory(HP* php) {assert(php);free(php->a); //释放动态开辟的数组php->a = NULL; //及时置空php->size = php->capacity = 0; //元素个数和容量置为0
}

三、建堆的时间复杂度

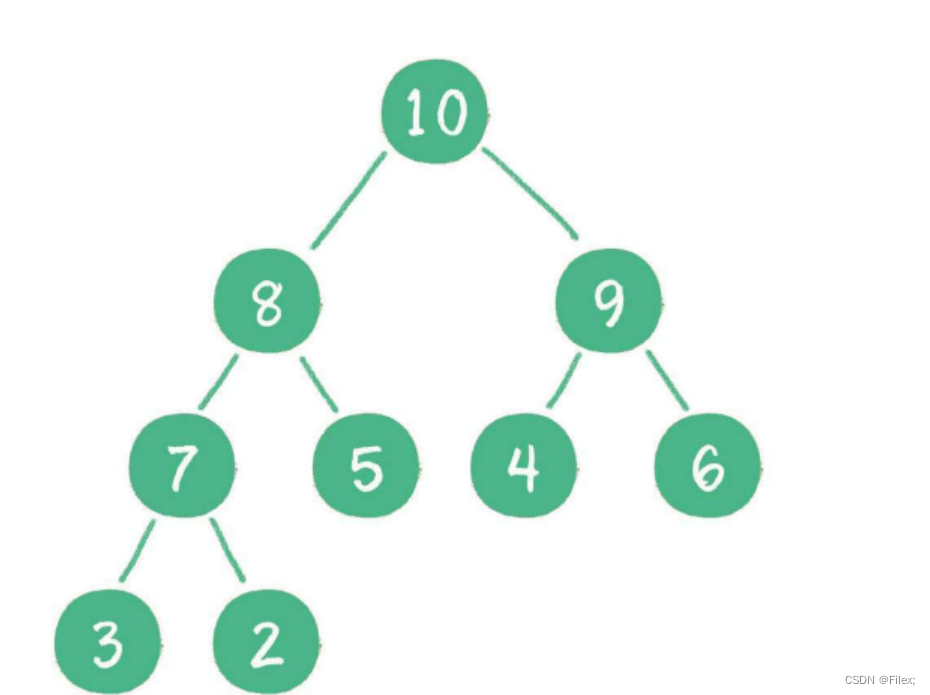
下面我们给出一个数组，这个数组逻辑上可以看做一颗完全二叉树，但是还不是一个堆，现在我们通过算法，把它构建成一个堆。根结点左右子树不是堆，我们怎么调整呢？

这里我们从倒数的第一个非叶子结点的子树开始调整，一直调整到根结点的树，就可以调整成堆。

int a[] = {1,5,3,8,7,6};

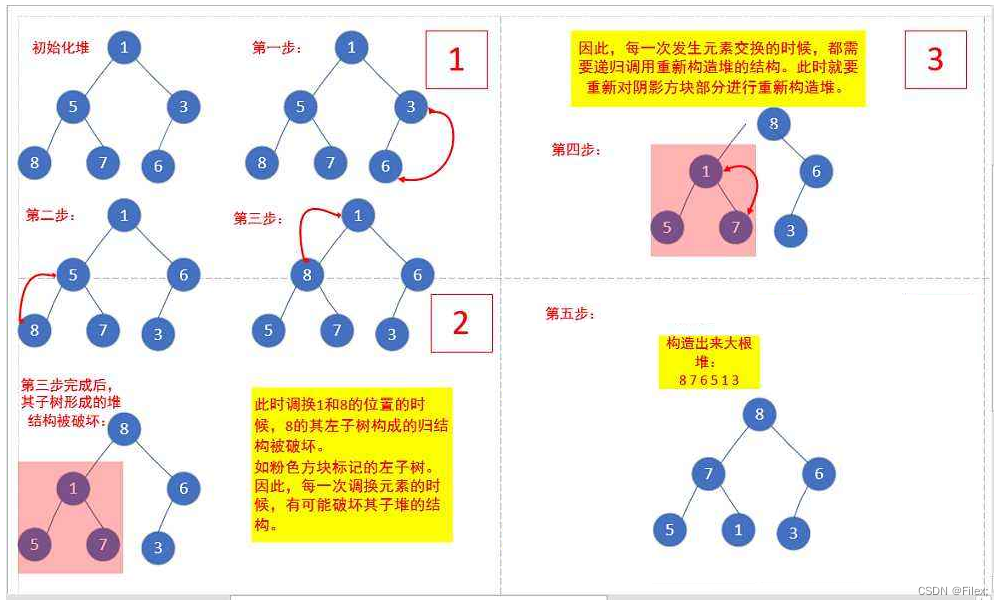
建堆代码：

从倒数第一个非叶子节点开始（最后一个节点的父亲）
n-1是最后一个节点的下标，(n-1-1)/2最后一个节点的父亲的下标
for (int i = (n - 1 - 1) / 2; i >= 0; --i) {AdjustDownBig(a, n, i);
}

那么建堆的时间复杂度又是多少呢？

因为堆是完全二叉树，而满二叉树也是完全二叉树，此处为了简化使用满二叉树来证明
(时间复杂度本来看的就是近似值，多几个结点不影响最终结果)：

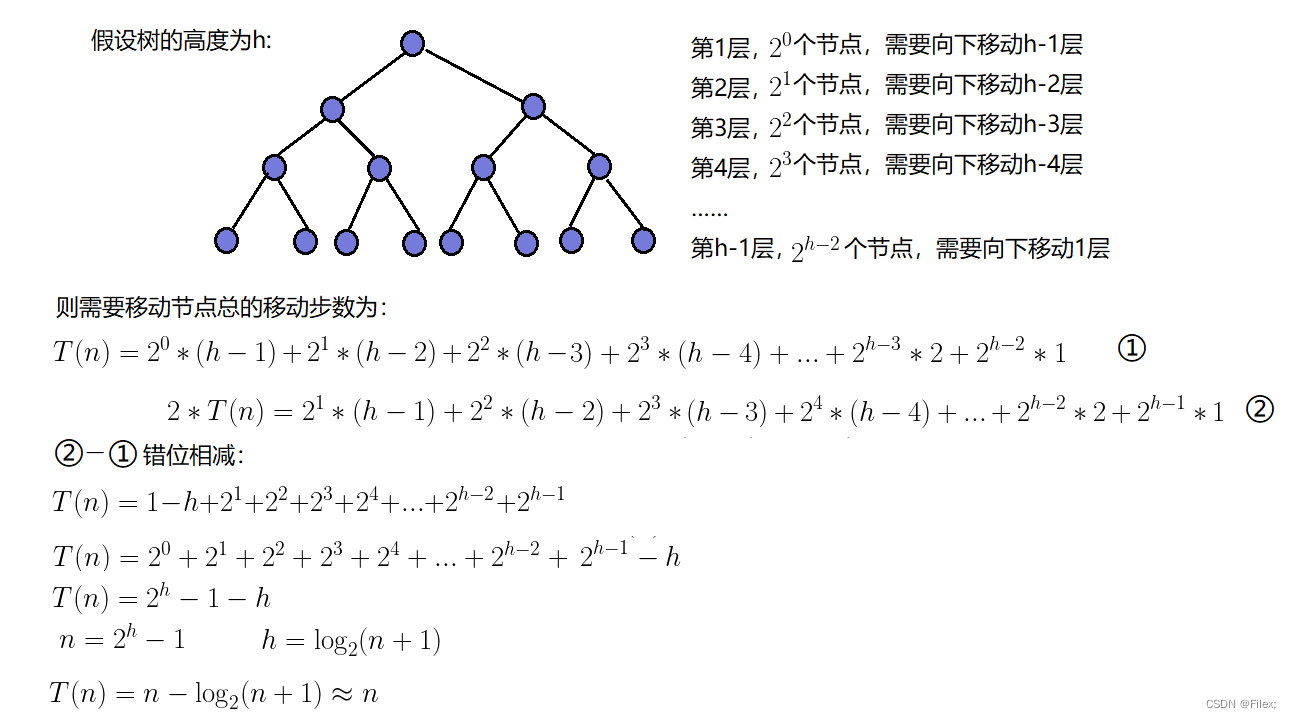
因此：建堆的时间复杂度为O(N)。

总结一下：

堆的向下调整算法的时间复杂度：O ( log N)
建堆的时间复杂度：O ( N )

四、堆排序

堆排序的基本思想是：

1)将无需序列构建成一个堆，根据升序降序需求选择大顶堆或小顶堆;
(升序建大堆，降序建小堆)
2)将堆顶元素与末尾元素交换，将最大元素"沉"到数组末端;
3)重新调整结构，使其满足堆定义，然后继续交换堆顶元素与当前末尾元素，反复执行调整+交换步骤，直到整个序列有序。

堆排序代码（以升序为例）：

void AdjustDownBig(HPDataType* a, int n, int parent)
{//建大堆//假设左孩子大int child = parent * 2 + 1;while(child < n){if ((child + 1) < n && a[child + 1] > a[child]){child++;}if (a[child] > a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}}void HeapSort(int* a, int n) {建堆：使用向下调整 --> O(N)从倒数第一个非叶子节点开始（最后一个节点的父亲）n-1是最后一个节点的下标，(n-1-1)/2最后一个节点的父亲的下标for (int i = (n - 1 - 1) / 2; i >= 0; --i) {AdjustDownBig(a, n, i);}升序 --> 建大堆size_t end = n - 1; 最后一个元素的下标while (end > 0){Swap(&a[0], &a[end]); 交换第一个元素和最后一个元素AdjustDownBig(a, end, 0);--end;}
}

总结一下：

堆排序是一种选择排序，整体主要由 构建初始堆 + 交换堆顶元素和末尾元素并重建堆 两部分组成。

其中构建初始堆经推导复杂度为 O ( n ) ，在交换并重建堆的过程中，需交换 n − 1 次，而重建堆的过程中，根据完全二叉树的性质，[ l o g 2 ( n − 1 ) , l o g 2 ( n − 2 ) . . . 1 ] 递减，近似为 n * log n 。

所以堆排序时间复杂度一般认为就是O(nlogn)级。

堆排序使用堆来选数，效率就高了很多。
时间复杂度：O ( N ∗ l o g N )
空间复杂度：O ( 1 )
稳定性：不稳定

五、二叉堆的应用——TopK问题

什么是 TOP-K?

TOP-K 问题：即求数据结合中前K个最大的元素或者最小的元素，一般情况下数据量都比较大。

比如：专业前 10 名、世界 500 强、富豪榜、游戏中前 100 的活跃玩家等。

最佳思路: 用堆来解决。

1）先将数组的前 K 个数建为 小堆。
2）将数组剩下的 N-K 个数依次与堆顶元素进行比较，若比堆顶元素大，则将堆顶元素替换为该元素，然后再进行一次向下调整，使其仍为小堆。
3)最后堆里面的 K 个数就是最大的前 K 个。

代码实现:

//调整算法里面的交换
void Swap(HPDataType* pa, HPDataType* pb) {HPDataType tmp = *pa;*pa = *pb;*pb = tmp;
}//向下调整算法 --> 构建小堆
void AdjustDownSmall(HPDataType* a, size_t size, size_t root) {size_t parent = root;size_t child = 2 * parent + 1; //默认左孩子最小while (child < size){//1.找出左右孩子中小的那个//如果右孩子存在，且右孩子小于size(元素个数)，那么就把默认小的左孩子修改为右孩子if (child+1 < size && a[child+1] < a[child]) {++child;}//2.把小的孩子去和父亲比较，如果比父亲小，就交换if (a[child] < a[parent]) {Swap(&a[child], &a[parent]);parent = child;child = 2 * parent + 1;}else {break; //如果孩子大于等于父亲，那么直接跳出循环}}
}void PrintTopK(int* a, int n, int k) {//1.建堆 --> 用a中前k个元素建小堆int* kminHeap = (int*)malloc(sizeof(int) * k);if (kminHeap == NULL) {printf("malloc fail\n");exit(-1);}//把数组的前K个数放进去（放进去的就是数组的前K个数，大小不一）for (int i = 0; i < k; ++i) {kminHeap[i] = a[i];}//k-1是最后一个数的下标，(k-1-1)/2就是倒数的第一个非叶子节点，也就是最后一个节点的父亲节点for (int j = (k - 1 - 1) / 2; j >= 0; --j) {//建小堆AdjustDownSmall(kminHeap, k, j);}//2.将剩余的n-k个元素依次与堆顶元素比较for (int i = k; i < n; ++i) {if (a[i] > kminHeap[0]) {kminHeap[0] = a[i];AdjustDownSmall(kminHeap, k, 0);}}free(kminHeap);
}

这种算法的时间复杂度为：O ( K + log K ∗ ( N − K ) ) ，当 N 非常大时，并且 K 很小，那么基本就是 O ( N ) .

空间复杂度：O ( K ) .

这样内存的消耗就取决于 K 的值了，就算要在 100 亿个数里面找到最大的 100 个数据，也只需要 400 字节的内存空间了！