写文章的初心主要是用来帮助自己快速的回忆这个模式该怎么用,主要是下面的UML图可以起到大作用,在你学习过一遍以后可能会遗忘,忘记了不要紧,只要看一眼UML图就能想起来了。同时也请大家多多指教。
装饰模式
是一种结构型模式。
目录
一、概述
1.1、主要的角色:
1.2、直观的理解装饰模式要干什么:
1.3、那么该如何思考呢?
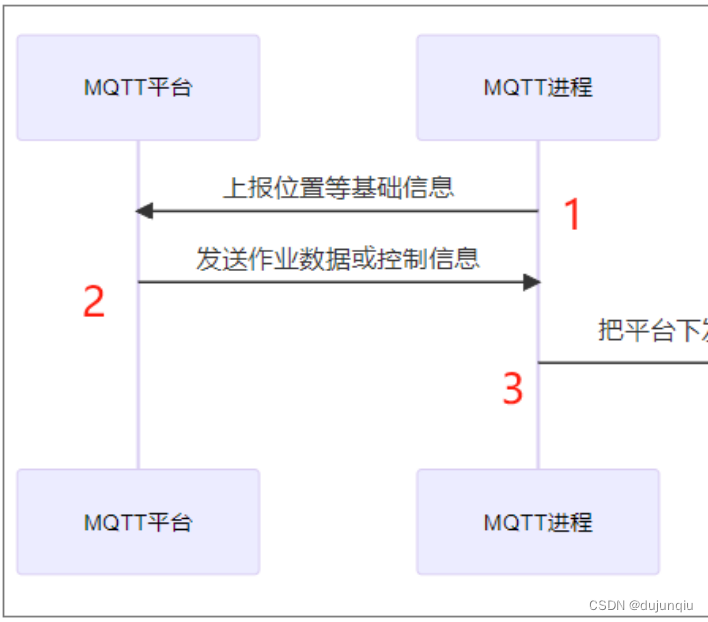
1.4、我先给出描述对象之间关系的UML图:
1.5、什么是断点?
二、举例代码实现
2.1、对象之间的关系用UML图表示如下:
2.2、代码如下(建议你在本地试一下,加深印象):
一、概述
1、需要把所需的功能按正确的顺序串联起来进行控制;2、动态地给一个对象添加一些额外的职责,就增加功能来说,装饰模式比生成子类更为灵活;3、装饰模式是为已有的功能动态的添加更多功能的一种方式;4、主要是给一个核心类 动态的添加各种功能。
1.1、主要的角色:
主要的角色分两种,但从代码(或技术)实现的角度看(为了充分使用面向对象语言的3大特性封装、继承、多态,还另外需要抽象类或接口)可能有4个:
- 组件类:组件类的抽象类或接口 + 组件类的实现类
- 装饰类:装饰类的抽象类或接口 + 装饰类的实现类
1.2、直观的理解装饰模式要干什么:
举个简单例子,之前是只运行对象A,现在新加了对象B和对象C,当我们希望要运行的对象应该由对象A到对象B再到对象C,也就是希望对象运行之间有严格的顺序要求时,就可以尝试使用装饰模式。如我们希望达到的效果是这样的:
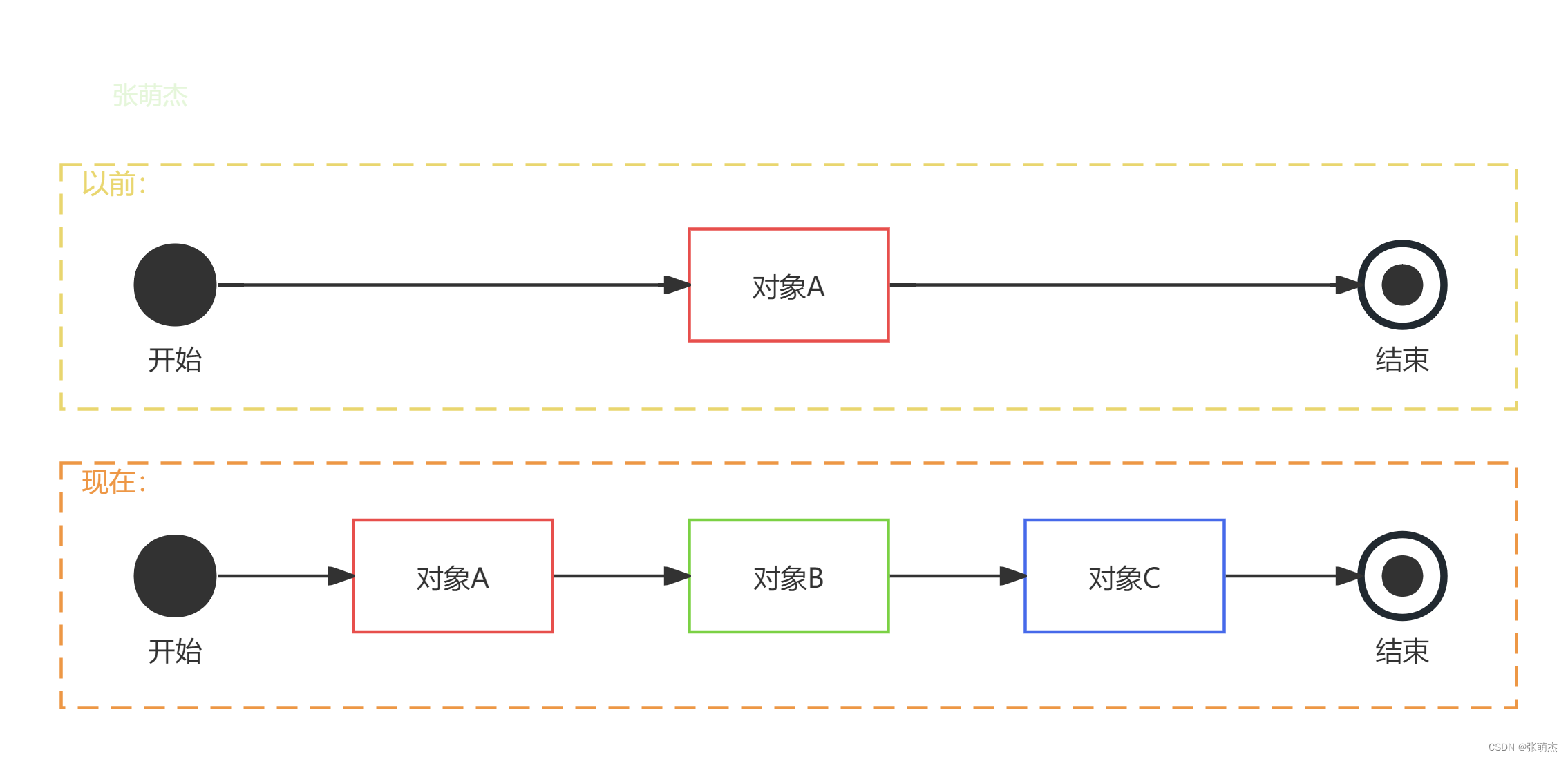
1.3、那么该如何思考呢?
可以从上可以看到,原先只有对象A,而对象B和对象C是后来加上的,且有严格的执行顺序,那么应用装饰模式后,我们可以认为:
- 对象A为组件类
- 对象B和对象C为装饰类,用来装饰对象A
除此之外,对于代码实现而言非常重要的东西是:
- 装饰类里的“断点”(这个词是我拍脑子想的,是为了帮助我们理解如何实现此模式而产生的,下面我会解释它是什么)。
1.4、我先给出描述对象之间关系的UML图:

1.5、什么是断点?
这是我从代码实现的角度提出的,所以要从代码的角度解释:
就拿上面的简单的举例来说,我们可以很明确地看到执行顺序是A-》B-》C,但实际代码实现上并非这样有前后顺序,而是你中有我、我中有你,解释图如下:
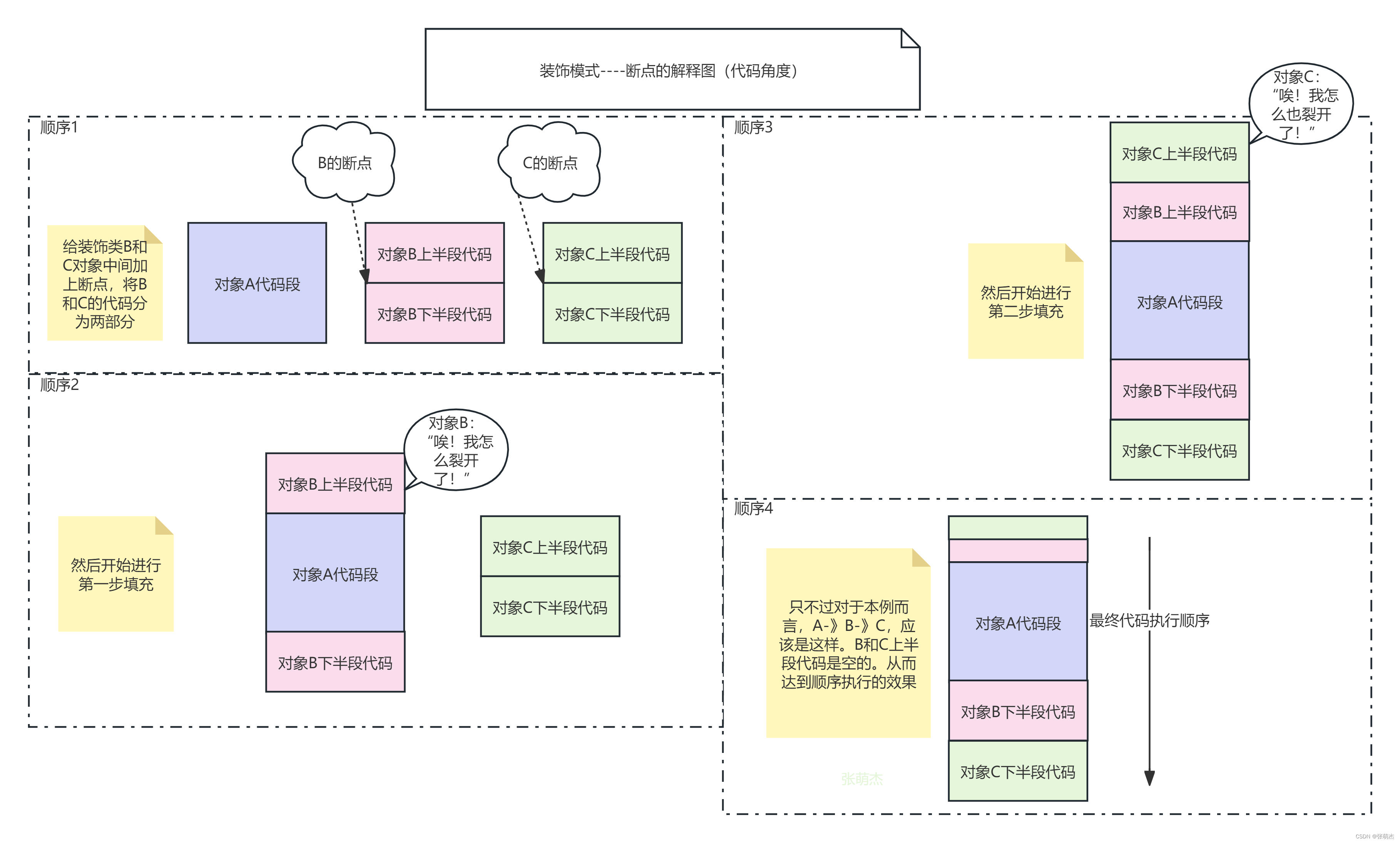
看懂上图我们就理解断点的意义了,同时也能发现装饰模式远比我们想象的更加灵活,不只是简单的A-》B-》C,就不再举例了。
需要说明的是,不同语言具体的实现方式略有不同,如:python的语法本身就支持装饰器,使用起来也更容易;而Java则需要创建装饰器父类,然后具体的装饰对象要继承父类,将调用父类的方法当做断点使用。但他们的共同点就是都有一个断点,这个断点可以用来插入别的类或对象的代码去运行。
二、举例代码实现
现有一个组件类和装饰类A、装饰类B,我们希望可以先运行组件类、再运行装饰类A、再运行装饰类B。
不再分析了,例子本身比较简单,而且上面概述当中也说的很清楚了。就直接给uml图和Java实现代码:
2.1、对象之间的关系用UML图表示如下:

2.2、代码如下(建议你在本地试一下,加深印象):
Java实现。
组件类的抽象类:
abstract class Component {public abstract void operation();
}
具体的组件类:
public class ConcreteComponent extends Component {@Overridepublic void operation() {System.out.println("具体组件对象的实际操作");}
}
装饰类的抽象类:
abstract class Decorator extends Component {protected Component component;public void setComponent(Component component) {this.component = component;}@Overridepublic void operation() {if (this.component != null) {component.operation();}}
}
装饰类A:
public class ConcreteDecoratorA extends Decorator {private String testA;@Overridepublic void operation() {super.operation(); //断点this.testA = "具体装饰对象A的独有操作";System.out.println(this.testA);}
}装饰类B:
public class ConcreteDecoratorB extends Decorator {@Overridepublic void operation() {super.operation(); //断点this.testB();}private void testB() {System.out.println("具体装饰对象B的独有操作");}
}
主程序(发起请求的类):
public class Main {public static void main(String[] args) {ConcreteComponent component = new ConcreteComponent();ConcreteDecoratorA concreteDecoratorA = new ConcreteDecoratorA();ConcreteDecoratorB concreteDecoratorB = new ConcreteDecoratorB();concreteDecoratorA.setComponent(component);concreteDecoratorB.setComponent(concreteDecoratorA);concreteDecoratorB.operation();}
}
这里就不再举例了,可以把上面的Java例子复制到你本地,运行main函数试一下加深理解。这些代码都是我自己学习的时候根据一些教材手敲的,不存在bug可以直接运行。
如果觉得本文还不错,就请点个赞给作者一点鼓励吧!如果有建议,也请评论指教和讨论!