一、基本概念

关系：定义在集合S上的关系指对于a，b∈S，若aRb为真，则a与b相关

等价关系：满足以下三个特性的关系R称为等价关系

(1)对称性，aRb为真则bRa为真；

(2)反身性,aRa为真;

(3)传递性,aRb为真，bRc为真，则aRc为真

等价类：等价类E是集合S的子集，其中E内的任意两个元素构成等价关系

不相交集：将集合S分为若干个等价类，等价类之间不包含相同的元素，对于x∈S，x只属于S中一个等价类。由于子集之间不包含相同的元素，将这样的集合称为不相交集。不相交集中主要基本操作是查找find和合并union，故常称为并查集。find查找给定元素所在的等价类，union将不在同一个等价类中的两个元素归并到一个等价类中，即将两个等价类归并为一个新的等价类。

 二、不相交集的实现

①线性表，线性表的第i个元素保存其所处等价类的名称，find时间复杂度O(1)，union时间复杂度O(N)

②采用树状结构，用一棵树表示一个并查集，每个并查集由树根唯一标识，则不相交集就构成一篇森林。判断结点处于哪一个并查集，需寻找其所在树的树根，因此采用双亲表示。在数组s[i]中，s[i]存储结点i的父结点的下标值，根结点则存特殊的-1。find就是向上找直到树根，时间复杂度O(logN)，union就是把一棵树作为另一颗树的子树，时间复杂度为O(1)

完成find的时间正比于从结点到根结点的路径长度，最坏的情况是O（N）[树退化为线性结构]，而find的性能一定程度上受到union的影响，因为在union过程中不考虑树的结构。改进思想是避免树增高，有两种思路：按规模归并，按高度归并,按高度归并可以保证find时间是对数级别。

 

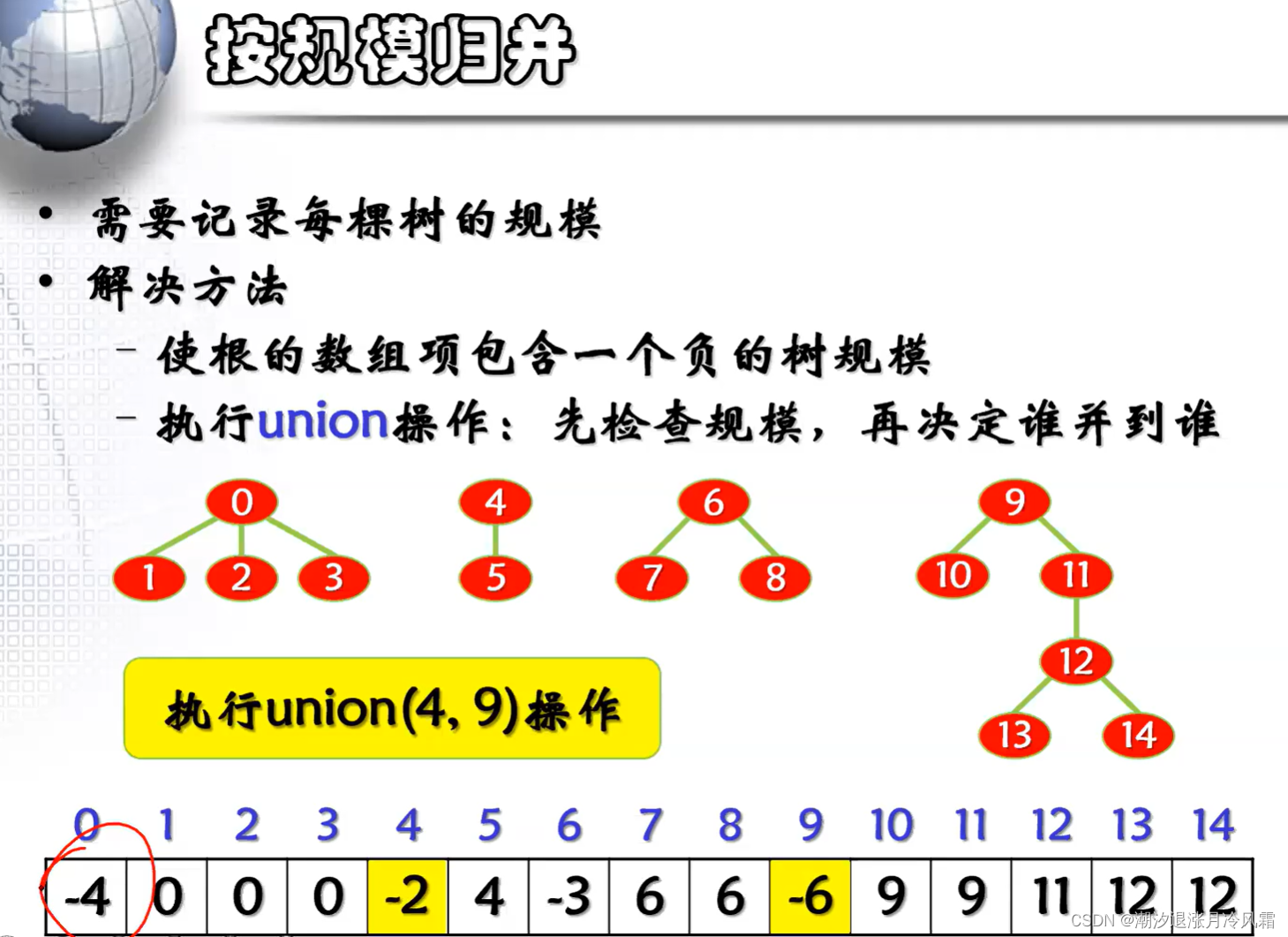
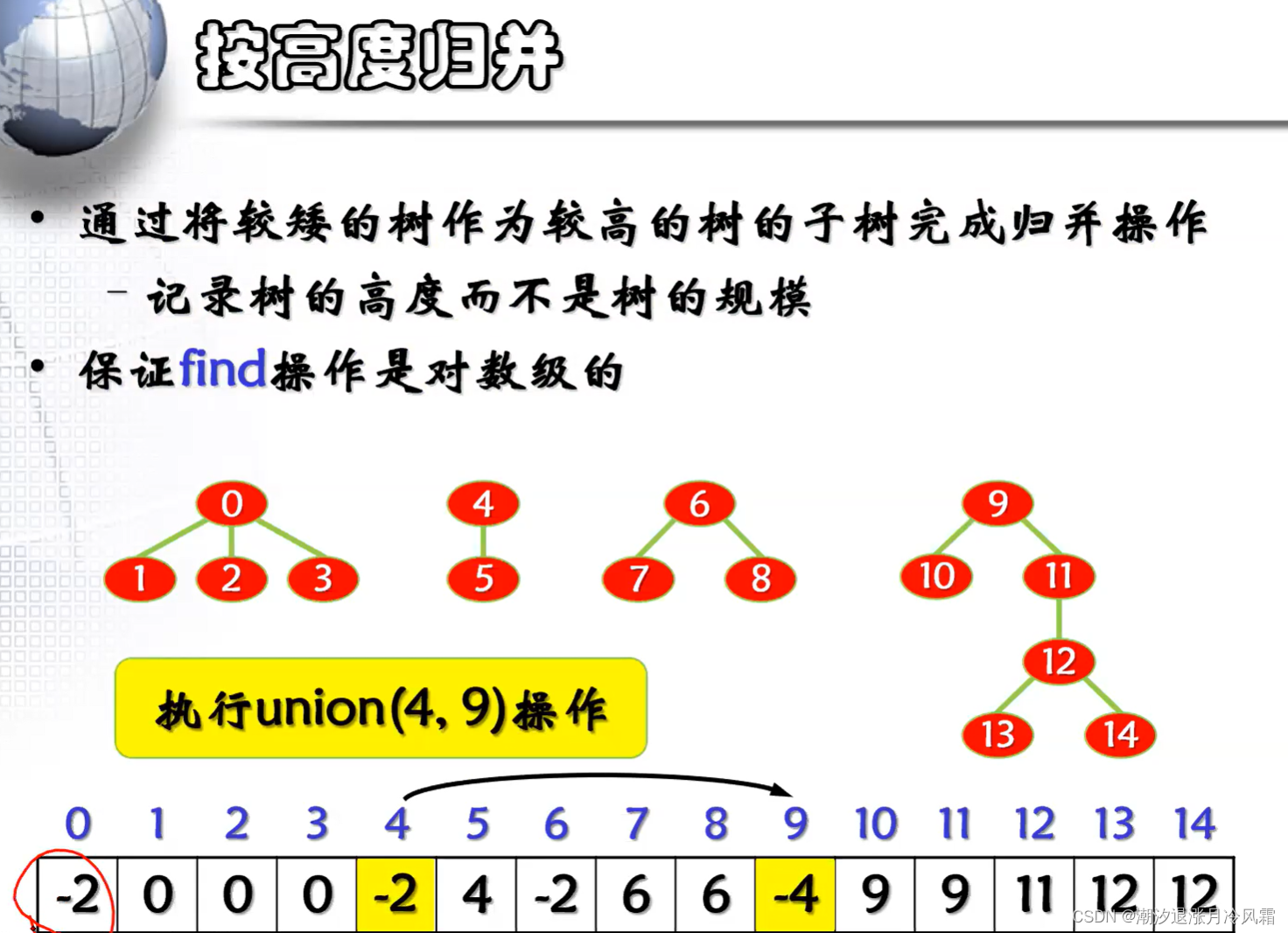
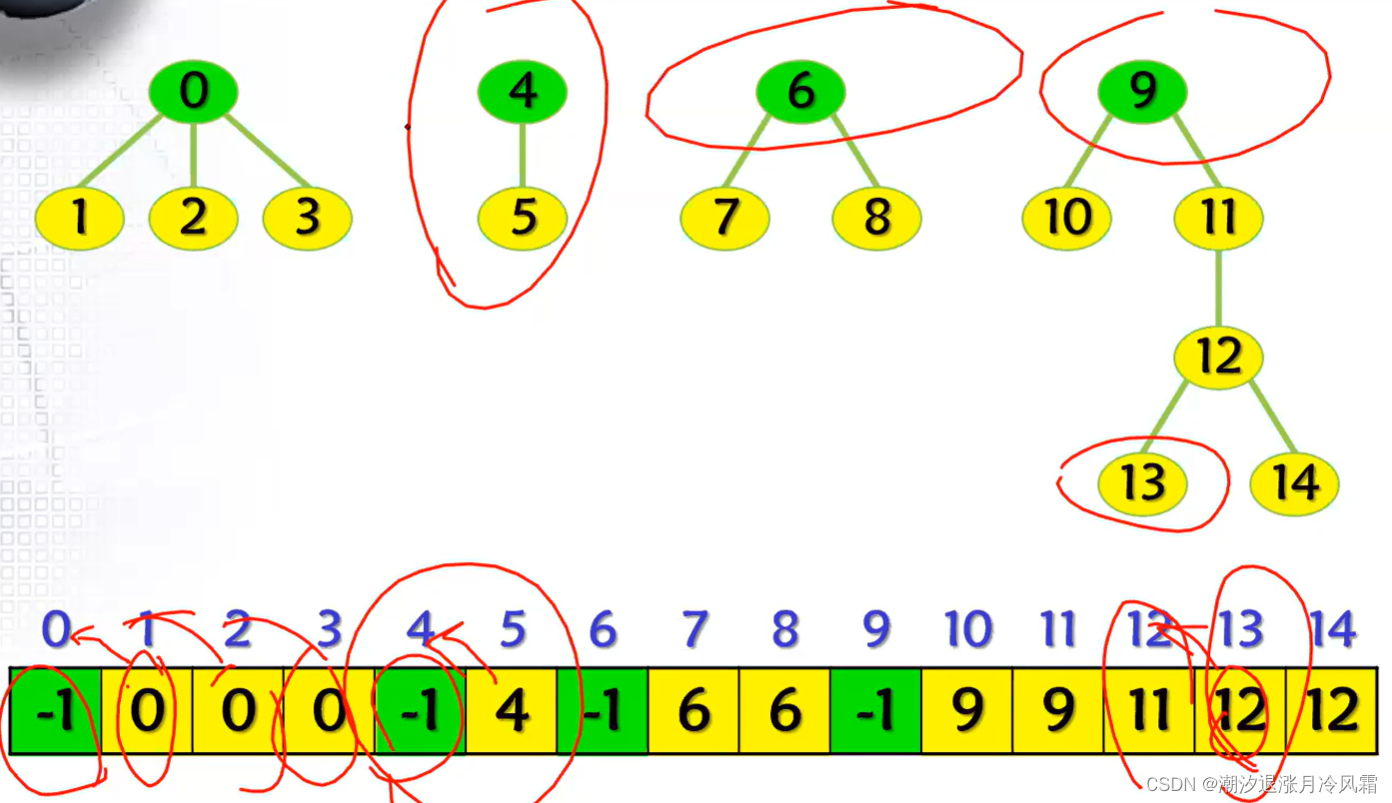
 最理想的情况是每一棵树的高度为2，只有根结点以及孩子结点，这时find的效率最高，尽管第一个改进能够提高find的效率，但是当两颗树高度接近时还是会使树的高度增加，引入第二个提高效率的方法：在find的时候进行路径压缩，即将路径上所有结点的父结点改为根结点。

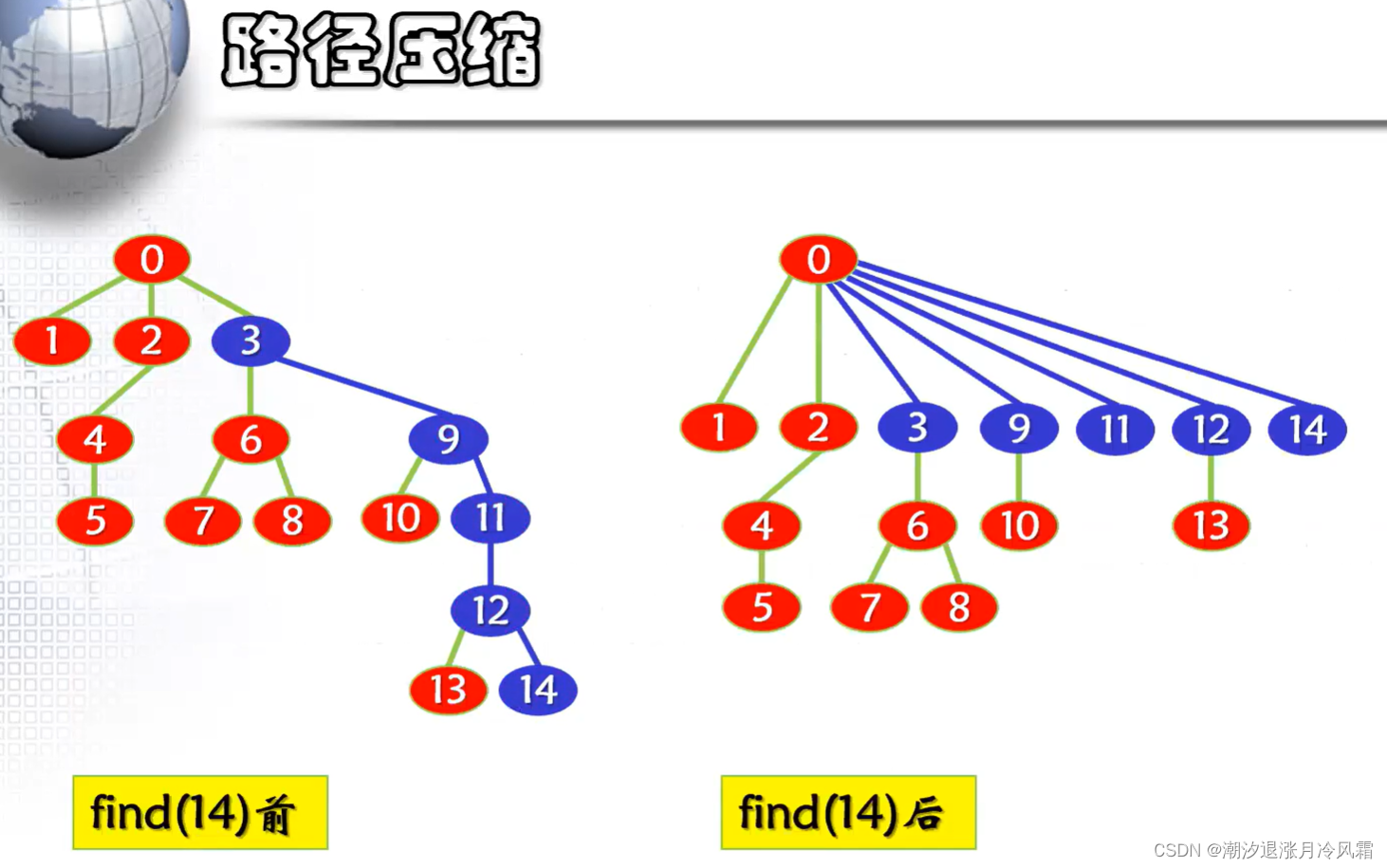
 Find(14)   return  parent[14]=Find(12)  0

Find(12)  return  parent[12]=Find(11)  0

Find(11)   return parent[11]=Find(9)  0

Find(9)    return  parent[9]=Find(3)   0

Find(3)  parent[0]=-15<0 return 0

 

三、不相交集的应用

 1.生成迷宫

将迷宫看成是M*N矩阵，每一个小块视为一个元素，左上角为入口，右下角为出口。块与块之间的连通关系属于等价关系，因此迷宫生成可以用并查集来实现。初始时块与块之间由墙分隔，通过随机拆墙的方法，逐渐连通迷宫中的区域，直至入口和出口连通时迷宫形成。

2.最近公共祖先问题

 

采取后序遍历的原因:先遍历两个结点，再遍历到其公共祖先

并查集的作用：每棵子树的根视作等价类的标志，当两个结点同属一棵树即同属一个等价类时，就找到了最近公共祖先。