数组基础-笔记

数组是非常基础的数据结构，实现运用和理解是两回事

数组是存放在连续内存空间上的相同类型的数据的集合

可以方便的通过下表索引的方式获取到下标下对应的数据。

举一个字符数组的例子：

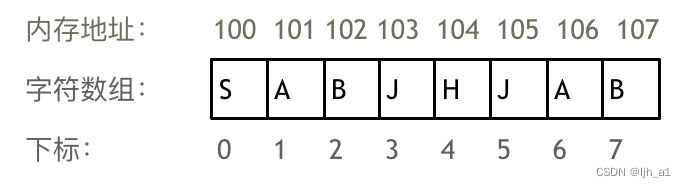
注意两点：

数组下标从0开始

数组内存空间的地址是连续的

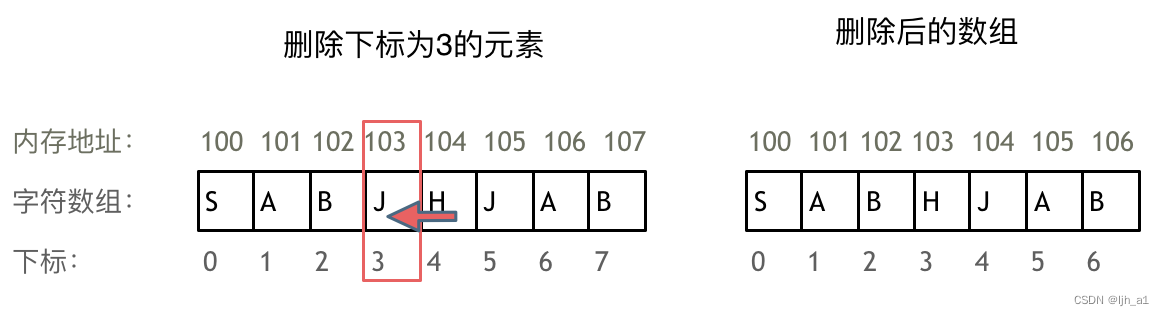
正因为数组的内存空间地址连续，索引删除或添加元素时，会移动其他元素地址

例如删除下标为3的元素，需要对下表为3的元素后面的虽有元素都要做移动操作。如图所示

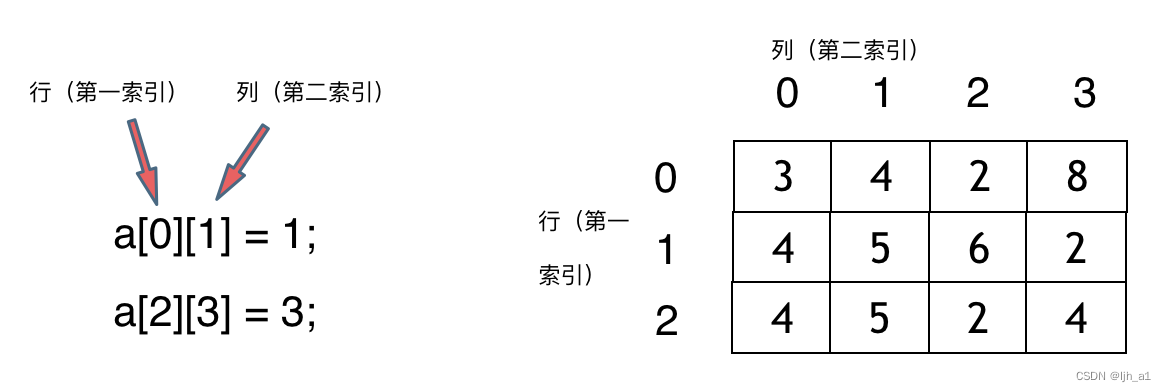
那二位数组在内存的空间地址是连续的么

不同编程语言的内存管理是不一样的。

1.二分查找

. - 力扣（LeetCode）

给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。

class Solution:def search(self, nums: List[int], target: int) -> int:left, right = 0, len(nums) - 1while left <= right:mid = (right - left) // 2 + leftnum = nums[mid]if num == target:return midelif num > target:right = mid - 1else:left = mid + 1return -1

复杂度分析

时间复杂度：O(log⁡n)O(\log n)O(logn)，其中 nnn 是数组的长度。
空间复杂度：O(1)O(1)O(1)。

2.移除元素

. - 力扣（LeetCode）

给你一个数组 nums 和一个值 val，你需要原地移除所有数值等于 val 的元素。元素的顺序可能发生改变。然后返回 nums 中与 val 不同的元素的数量。

假设 nums 中不等于 val 的元素数量为 k，要通过此题，您需要执行以下操作：

更改 nums 数组，使 nums 的前 k 个元素包含不等于 val 的元素。nums 的其余元素和 nums 的大小并不重要。
返回 k。

def remove_element(nums, val):i = 0    # 初始化一个指针 i 用于遍历数组for j in range(len(nums)):    # 遍历数组if nums[j]!= val:    # 如果当前元素不等于目标值nums[i] = nums[j]    # 将当前元素赋值给指针 i 位置的元素i += 1return i    # 返回不等于目标值的元素个数

在这里，通过遍历数组，当遇到不等于 val 的元素时，就将其覆盖到前面指针 i 所指向的位置，这样就逐步将不等于 val 的元素往前移动，而等于 val 的元素则被后面的非 val 元素覆盖掉，从而实现了原地移除等于 val 的元素。

如果要获取变更后的数组，可以加一个nums[:i],做截断。

 nums[:i]  # 返回数量和变更后的数组片段

3. 有序数组的平方

. - 力扣（LeetCode）

给你一个按 非递减顺序 排序的整数数组 nums，返回 每个数字的平方 组成的新数组，要求也按 非递减顺序 排序。

输入：nums = [-4,-1,0,3,10]
输出：[0,1,9,16,100]
解释：平方后，数组变为 [16,1,0,9,100]
排序后，数组变为 [0,1,9,16,100]

def sorted_squares(nums):# 初始化结果列表result = []# 初始化左右指针left = 0right = len(nums) - 1# 当左指针小于等于右指针时循环while left <= right:# 如果左指针对应值的平方大于右指针对应值的平方if nums[left] ** 2 > nums[right] ** 2:result.append(nums[left] ** 2)  # 将左指针对应值的平方加入结果列表left += 1  # 左指针右移else:result.append(nums[right] ** 2)  # 将右指针对应值的平方加入结果列表right -= 1  # 右指针左移# 反转结果列表使其非递减排序return result[::-1]

4.长度最小的子数组

. - 力扣（LeetCode）

给定一个含有 n 个正整数的数组和一个正整数 target 。

找出该数组中满足其总和大于等于 target 的长度最小的 连续子数组

[numsl, numsl+1, ..., numsr-1, numsr] ，并返回其长度。如果不存在符合条件的子数组，返回 0 。

def min_sub_array_len(target, nums):# 初始化左指针left = 0# 初始化当前子数组和cur_sum = 0# 初始化最小长度为无穷大min_len = float('inf')# 遍历数组for right in range(len(nums)):cur_sum += nums[right]  # 将当前元素加入和# 当和大于等于目标值时while cur_sum >= target:min_len = min(min_len, right - left + 1)  # 更新最小长度cur_sum -= nums[left]  # 减去左指针指向的元素left += 1  # 左指针右移# 如果最小长度还是无穷大，说明没有找到符合条件的子数组，返回 0return min_len if min_len!= float('inf') else 0

该算法的时间复杂度为 O(n)。

在这个算法中，我们使用了一个滑动窗口来遍历数组。每次移动窗口时，我们需要计算当前窗口内元素的总和，并判断是否满足条件。这个过程需要遍历窗口内的所有元素，因此时间复杂度为 O(n)。

具体来说，在每次循环中，我们需要执行以下操作：

计算当前窗口的和：cur_sum += nums[right]，这需要 O(1)的时间。
判断当前窗口的和是否大于等于目标值：while cur_sum >= target，这需要 O(1)的时间。
更新最小长度：min_len = min(min_len, right - left + 1)，这需要 O(1)的时间。
移动窗口：cur_sum -= nums[left]，left += 1，这需要 O(1)的时间。

因此，总的时间复杂度为 O(n)，其中 n 为数组的长度。

5.螺旋矩阵II

. - 力扣（LeetCode）

给你一个正整数 n ，生成一个包含 1 到 n2 所有元素，且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。

def generate_matrix(n):# 创建一个 n x n 的全 0 矩阵matrix = [[0] * n for _ in range(n)]# 初始化当前数字num = 1# 上下左右边界top = 0bottom = n - 1left = 0right = n - 1while num <= n * n:# 从左到右填充上边界行for i in range(left, right + 1):matrix[top][i] = numnum += 1top += 1# 从上到下填充右边界列for i in range(top, bottom + 1):matrix[i][right] = numnum += 1right -= 1# 从右到左填充下边界行for i in range(right, left - 1, -1):matrix[bottom][i] = numnum += 1bottom -= 1# 从下到上填充左边界列for i in range(bottom, top - 1, -1):matrix[i][left] = numnum += 1left += 1return matrix