- 实验目的:
- 掌握矩法估计与极大似然估计的求法;
- 了解估计量的优良性准则:无偏性、有效性、相合性(一致性);
- 学会利用R软件完成一个正态总体均值和两个正态总体均值差的区间估计;
- 学会利用R软件完成两个成对数据均值差的区间估计;
- 学会利用R软件完成一个总体比例和两个总体比例差的区间估计;
- 掌握大样本数据关于单个总体均值和总体比例的样本容量的确定方法。
实验内容:
(习题5.1)下表列出 50 个抽取自二项分布总体 B(n, p) 的数据(数据存放在 binom . data件中),试用矩估计方法估计参数n和p。
来自二项分布总体的数据
| 15 | 16 | 14 | 15 | 16 | 11 | 15 | 15 | 12 | 14 | 14 | 14 | 12 | 14 | 12 | 15 | 14 |
| 14 | 12 | 14 | 15 | 17 | 18 | 10 | 13 | 12 | 15 | 17 | 16 | 18 | 17 | 12 | 10 | 15 |
| 13 | 12 | 14 | 16 | 16 | 16 | 15 | 11 | 13 | 15 | 16 | 17 | 14 | 11 | 16 | 17 |
解:若将n作为未知参数,则需要同时考虑一阶矩和二阶矩。
总体的一阶矩和二阶矩分别为:
a1 =E(X)= np, a2 =E(X 2)= var(X)+(E(x))2 = np(1-p)+(np)2,
根据矩估计的基本思想,a1 = A1,a2 = A2,(其中
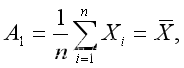
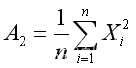 )
)
即有
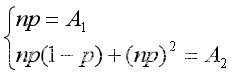
解上述方程组,可得
 ,
,![]() 。
。
以下请根据上式完成R程序,计算出参数n和p的矩估计量的值
(参考n = 20.0284,p = 0.713986)
源代码:
# 读取数据data <- scan("C:/Users/黄培滇/Desktop/R语言生物统计学/chap05/binom.data")# 计算参数估计m1 <- mean(data)m2 <- mean(data^2)p=1+m1-m2/m1n=m1/ppn
运行结果或截图:

(习题5.2)设总体X的分布密度函数为

从总体X抽取的样本为:
0.1 0.2 0.9 0.8 0.7 0.7 0.6 0.5
求参数a 的极大似然估计量![]() 。
。
解:
设X1,X2,…,Xn 为其样本,只需要考虑xÎ(0, 1)部分。依题意,
此分布的似然函数为 L(a ; x) =
相应的对数似然函数为 ln L(a ; x) = n ln(a +1)+ a ln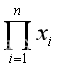
令
 ln
ln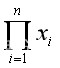 =0
=0
解此似然方程得到
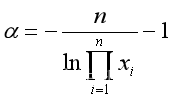 ,或写为
,或写为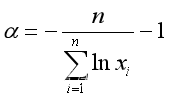
容易验证
,从而a 使得L达到极大,即参数a 的极大似然估计量 。
。
以下请根据上式完成R程序,计算出参数a 的极大似然估计量![]() 的值。
的值。
源代码:
data<-c(0.1,0.2,0.9,0.8,0.7,0.7,0.6,0.5)n<-length(data)alpha_hat<-n/(-sum(log(data)))-1alpha_hat运行结果或截图:

补充:求参数a 的矩估计量![]() 。由于只有一个参数,因此只需要考虑a1 = A1,即E(X)=
。由于只有一个参数,因此只需要考虑a1 = A1,即E(X)=![]()
而由E(X)的定义有:E(X)=

因此 ,解得
,解得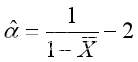 。
。
以下请根据上式完成R程序,计算出参数a 的矩估计量![]() 的值,并与其极大似然估计量的值进行比较。
的值,并与其极大似然估计量的值进行比较。
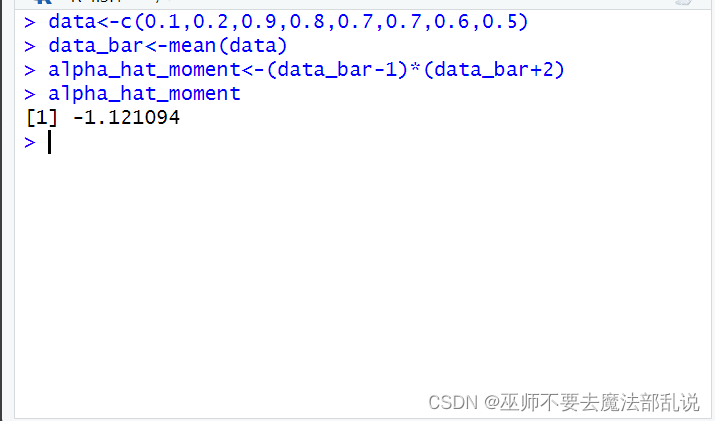
源代码:
data<-c(0.1,0.2,0.9,0.8,0.7,0.7,0.6,0.5)data_bar<-mean(data)alpha_hat_moment<-(data_bar-1)*(data_bar+2)alpha_hat_moment运行结果或截图:
(习题5.4)为研究新生儿出生时的体重,随机地选取了某妇产医院的100个新生儿,其样本均值为3338g,样本标准差为629g。试计算新生儿平均体重的置信水平为95%的置信区间。
提示:参考例5.6
解:源代码及运行结果:(复制到此处,不要截图)
birth_bar<-3338birth_S<-629n<-100alpha<-0.05z<-qnorm(1-alpha/2)c(birth_bar - birth_S/sqrt(n)*z,birth_bar + birth_S/sqrt(n)*z)结论:

(习题5.5)某妇产医院有意估计产妇在该医院住院的平均天数,在过去的年份中随机抽取了 36位孕妇,每位孕妇住院天数取整后如下表所示(数据存放在 hospital.data 文件中)。使用这些数据构建 95% 的置信区间,估计在该医院生小孩的所有孕妇的平均住院天数。
提示:参考例5.10。由于此题是小样本数据,也可以直接使用t.test()函数。
解:源代码及运行结果:(复制到此处,不要截图)
> H_data<-scan("C:\\Users\\黄培滇\\Desktop\\R语言生物统计学\\chap05\\hospital.data")Read 36 items> H_bar<-mean(H_data);S<-sd(H_data)> n<-length(H_data)> alpha<-0.05> t<-qt(1-alpha/2,df = n-1)> c(H_bar - S/sqrt(n)*t,H_bar + S/sqrt(n)*t)[1] 2.910812 3.700299
结论:
即95%的产妇在医院的平均住院时间在2~3天
(习题5.8)已知某种灯泡寿命服从正态分布,在某星期所生产的该灯泡中随机抽取10 只,测得其寿命(单位:小时)为
1067 919 1196 785 1126 936 918 1156 920 948
求灯泡寿命平均值的置信度为0.95的单侧置信下限。
提示:此题是一个正态总体的区间估计问题,且由于总体方差未知,因此可以直接使用R语言中t.test()函数进行分析。参考例5.11,单侧置信下限,t.test()函数中的参数alternative="greater"。
解:源代码及运行结果:(复制到此处,不要截图)
> L<-c(1067,919,1196,785,1126,936,918,1156,920,948)> t.test(L,alternative="greater")One Sample t-test
data: L
t = 23.969, df = 9, p-value = 9.148e-10
alternative hypothesis: true mean is greater than 0
95 percent confidence interval:
920.8443 Inf
sample estimates:
mean of x
997.1
结论:
即这批灯泡中95%的平均寿命在997.1小时以上
(习题5.11)某调查公司对 902 名高尔夫女选手进行了一项调查,以了解女选手怎样看待自己在比赛中的安排。调查结果显示 397 名女选手对下午茶的时间感到满意。(1) 试计算所有女选手对下午茶的时间感到满意的置信区间,这里取置信水平为 0.95; (2) 如果使用binom. test ()函数精确计算两者相差多少?
提示:参考例5.12。
解:源代码及运行结果:(复制到此处,不要截图)
> my<-397;w<-902> p<-my/w;q<-1-p> alpha<-0.05;z<-qnorm(1-alpha/2)> c(p-z*sqrt(p*q/w),p+z*sqrt(p*q/w))0.4077379 0.4725281
> binom.test(my,w)Exact binomial test
data: my and w
number of successes = 397, number of trials =
902, p-value = 0.0003617
alternative hypothesis: true probability of success is not equal to 0.5
95 percent confidence interval:
0.4074246 0.4732337
sample estimates:
probability of success
0.440133
结论:
即在女子高尔夫比赛时间安排中,女选手对下午茶的时间满意总体比例在0.407~0.473的概率是95%
两者相差0.440133
(续习题5.12)如果希望新生儿的平均体重与总体均值的边际误差不超过 100 ,应从该妇产医院随机地选取多少名新生儿?
提示:例5.13。
解:源代码及运行结果:(复制到此处,不要截图)
> birth_S<-629> E<-100> alpha<-0.05> z<-qnorm(1-alpha/2);> (n<-z^2*birth_S^2/E^2)[1] 151.9839
结论:
说明还需要从妇产医院再随机抽取52名新生儿
(习题5.13)某汽车营销公司计划估计某地区拥有小汽车家庭所占的比重,要求边际误差不超过5%,置信水平取 90%, 问应抽取多少样本?公司调查人员认为,拥有小汽车家庭的实际比重不会超过 20%,如果这一结论成立,应抽取多少样本?
提示:例5.14。
解:源代码及运行结果:(复制到此处,不要截图)
> p<-0.2;E<-0.05;alpha<-0.1> z<-qnorm(1-alpha/2)> (n<-z^2*p*(1-p)/E^2)[1] 173.1548
结论:
即需要随机抽取174个家庭
(习题5.16)甲、乙两种稻种分别播种在10块试验田中,每块试验田甲、乙稻种各种一半。假设两稻种产量X, Y均服从正态分布,且方差相等。收获后10块试验田的产量如下所示(单位:千克)。
| 甲种 | 140 | 137 | 136 | 140 | 145 | 148 | 140 | 135 | 144 | 141 |
| 乙种 | 135 | 118 | 115 | 140 | 128 | 131 | 130 | 115 | 131 | 125 |
求出两稻种产量的期望差m1-m2的置信区间(a =0.05)。
提示:此题是两个正态总体的区间估计问题,且由于两总体方差未知,因此可以直接使用R语言中t.test()函数进行分析。t.test()可做两正态样本均值差的估计。注意此例中两样本方差相等。
解:源代码及运行结果:(复制到此处,不要截图)
> a<-c(140,137,136,140,145,148,140,135,144,141)> b<-c(135,118,115,140,128,131,130,115,131,125)> a_bar<-mean(a);Sa<-sd(a);na<-length(a)> b_bar<-mean(b);Sb<-sd(b);nb<-length(b)> alpha<-0.05;z<-qnorm(1-alpha/2)> S<-sqrt(Sa^2/na + Sb^2/nb)> c(a_bar - b_bar - z*S,a_bar - b_bar + z*S)[1] 7.956516 19.643484
结论:
即两个稻种产量的期望差在95%的置信水平下位于[7.96, 19.64]这个区间内。
(习题5.17)甲、乙两组生产同种导线,现从甲组生产的导线中随机抽取4根,从乙组生产的导线中随机抽取5根,它们的电阻值(单位:W)分别为
| 甲组 | 0.143 | 0.142 | 0.143 | 0.137 | |
| 已组 | 0.140 | 0.142 | 0.136 | 0.138 | 0.140 |
假设两组电阻值分别服从正态分布N(m1, s 2)和N(m1, s 2),s 2未知。试求m1-m2的置信区间系数为0.95的区间估计。
提示:此题是两个正态总体的估计问题,且由于两总体方差未知,因此可以直接使用R语言中t.test()函数进行分析。t.test()可做两正态样本均值差的估计。注意此例中两样本方差相等。
解:源代码及运行结果:(复制到此处,不要截图)
> x <- c(0.143, 0.142, 0.143, 0.137)> y <- c(0.140, 0.142, 0.135, 0.138, 0.140)> x_bar <- mean(x)> Sx <- sd(x)> nx <- length(x)> y_bar <- mean(y)> Sy <- sd(y)> ny <- length(y)> Sw2 <- ((nx - 1) * Sx^2 + (ny - 1) * Sy^2) / (nx + ny - 2)> S <- sqrt(Sw2 * (1/nx + 1/ny))> alpha <- 0.05> t <- qt(1 - alpha/2, nx + ny - 2)> conf_interval <- c(x_bar - y_bar - t*S, x_bar - y_bar + t*S)> conf_interval[1] -0.002104423 0.006604423
结论:
两组之差的置信区间系数为0.95的区间估计为-0.002,0.007
思考:
常用的点估计的方法有哪些?
矩估计法;极大似然估计法;
估计量的优良性准则有哪些?
估计量的优良性准则:无偏性、有效性、相合性(一致性)
在对单个总体样本均值进行区间估计时,可以使用Z统计量和T统计量,这两个统计量分别在什么情况下使用?
总体标准差已知且样本容量较大,则可以使用Z统计量进行区间估计;
如果总体标准差未知或者样本容量较小,则应使用T统计量进行区间估计
对于单个总体比例的区间估计问题,涉及到其实是二项分布。但是当满足
n大于等于30 条件时,也可以近似使用正态分布来计算。
对于单个总体比例的区间估计,涉及的是二项分布。因此在R语言中,可以使用binom.test()函数进行区间估计,它是精确检验函数,通常用于小样本数据;当处理大样本数据时,在R语言并没有使用正态分布函数,而是使用了 prop.test() 分布函数?同样,在使用这个分布函数时,仍然需要满足 样本容量足够大,且满足二项分布近似正态性 条件。
在对两个总体样本均值差进行区间估计时,可以使用Z统计量和T统计量,这两个统计量分别在什么情况下使用?
两个总体标准差已知,用Z统计量
两个总体标准差未知,用T统计量
在对两个总体样本均值差进行区间估计时,如果使用了T统计量,还要进一步考虑两个总体的 方差 是否相同 ,来分别使用不同的T统计量。