题目链接：209. 长度最小的子数组 - 力扣（LeetCode）

题目分析

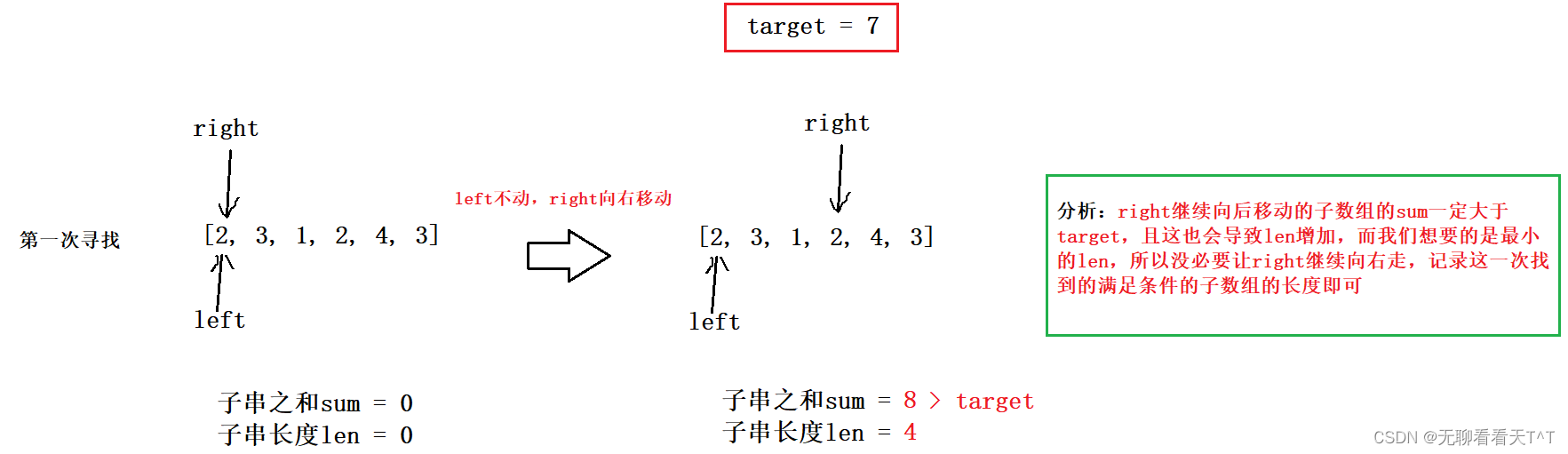
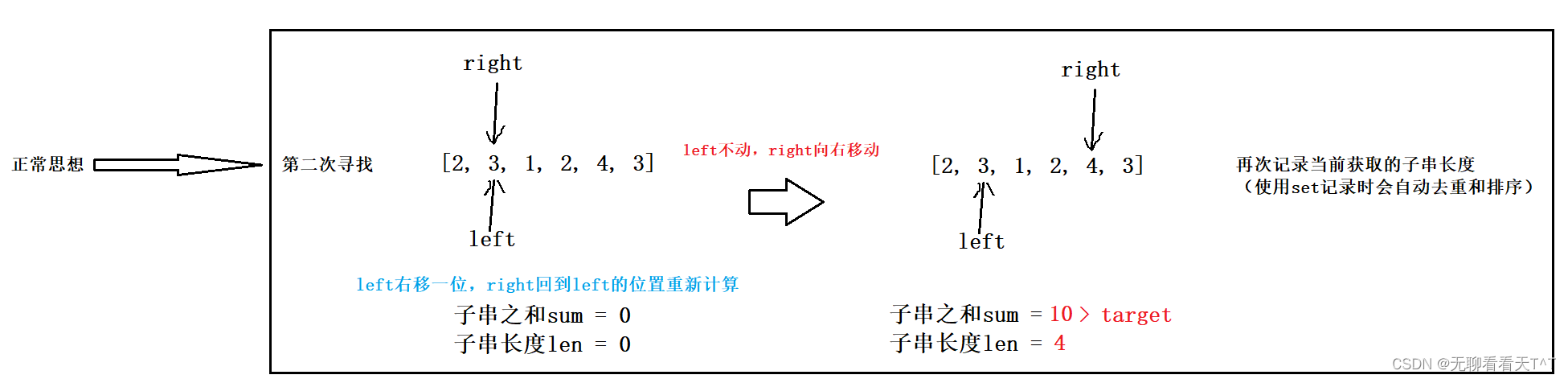
由暴力枚举引申到滑动窗口的画图分析过程

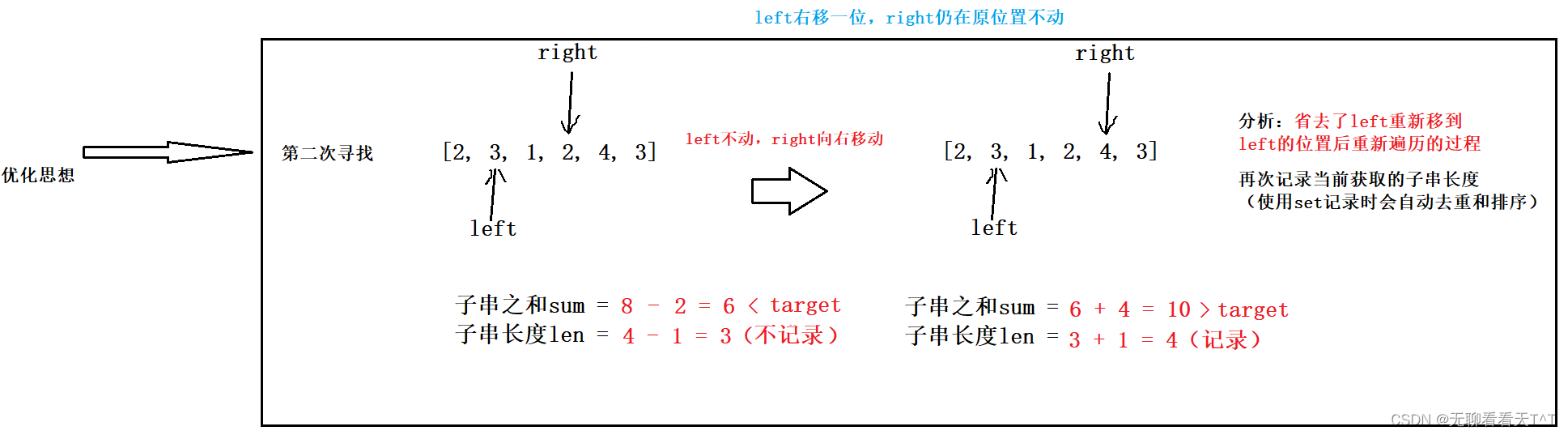
优化版本（滑动窗口）

滑动窗口的使用场景：单调性（一定是递增或递减的情况） + 可以不回退的同向双指针（可能是int left和right，可能是是int *left和*right）

使用模板： 

class Solution {
public:int minSubArrayLen(int target, vector<int>& nums) {int n = nums.size(),sum = 0,len = INT_MAX;for(int left = 0,right = 0;right < n;right++){sum += nums[right];//进窗口while(sum >= target){len = min(len,right - left + 1);//更新结果, right-left+1表示符号条件的子数组长度sum -= nums[left++];//出窗口（如果出窗口后rigth仍然小于n就重新进窗口）}}return len == INT_MAX ? 0 : len;//需要加一个判断条件，如果没有满足的子数组应该返回0//但初始化时将len设置为INT_MAX，故如果最后len仍为INT_MAX时就返回0}
};

补充：因为当前我们只要一个最小的子数组长度，不是取所有我们统计到的满足条件的子数组的中间值的那种要求，所以不用set记录结果，直接当遇到更小的len时更新len即可，且len的初始值太小，因为如果答案的最小子数组长度为5而你len的初始值为2，那么就一直得不到正确结果，所以最好将其设置一个足够大的值比如INT_MAX

时间复杂度： O（N）

时间复杂度分析：

①代码是两层循环嵌套，暴力枚举时的确是O（N^2）因为right每次还要回到left的新位置最坏情况是right每走N次返回left，left需要走N次才能到达末尾，即（N * N ）= O（N^2）

②但滑动窗口中的right只会接着上次的结果继续移动，且当某条件满足时left继续右移，最坏的情况就是当right移动n次到数组末尾时才满足条件，然后left才会去移动N次也到达数组末尾，即O（N + N ）= O（2N）=  O（N），

问题：为什么这样就可以得到正确结果？暴力枚举是将所有结果都枚举出来然后选出符号要求的结果，滑动窗口并没有枚举出所有结果，它是如何保证正确性的？

解释：滑动窗口利用单调性，规避了很多没有必要的枚举行为，上述案例中在确定一个满足条件的子数组长度后，因为是right继续向后走sum一定会增加且一直大于target，这时还继续向后走统计出一个长度为5的子数组{2，3，1，2，4}是没有必要的，前面已经有了一个长度为4的子数组{2，3，1，2}，长度为5甚至是6的子数组肯定不会是最终结果，不枚举也罢

还不懂就画一个小窗口自己套在数组上试一试

~over~