最小二乘法拟合消除趋势项
消除趋势项函数
在MATLAB的工具箱中已有消除线性趋势项的detrend函数;再介绍以最小二乘法拟合消除趋势项的polydetrend 函数。
函数:detrend功能:消除线性趋势项
调用格式:y=detrend(x)说明:输入参数x是带有线性趋势项的信号序列,输出参数y是消除趋势项的序列。
函数:polydetrend功能:最小二乘法拟合消除多项式的趋势项
调用格式:[y,xtrend]=polydetrend(x,fs,m)说明:输人参数x是带有趋势项的信号,fs是采样频率,m是调用本函数时设置的多项式阶次。输出参数y是消除趋势项后的信号序列,xtrend是叠加在信号上的趋势项序列。函数polydetrend的程序清单如下:
function [y,xtrend]=polydetrend(x, fs, m)
x=x(:); % 把语音信号x转换为列数据
N=length(x); % 求出x的长度
t= (0: N-1)'/fs; % 按x的长度和采样频率设置时间序列
a=polyfit(t, x, m); % 用最小二乘法拟合语音信号x的多项式系数a
xtrend=polyval(a, t); % 用系数a和时间序列t构成趋势项
y=x-xtrend; % 从语音信号x中清除趋势项基线漂移的修正
1.概 述
在实际采集到的信号中经常会发生基线漂移,这可能是由多种原因造成的。本案例将介绍在心电图检测中,若由于病人身体的轻微活动造成了心电图信号的基线漂移,则在后期处理中就可以用最小二乘法拟合消除消除基线的漂移。
2.实例
读入已知的心电图ecgdata2.mat数据,用最小二乘法拟合消除基线的漂移。程序清单如下:
clear all; clc; close all;
load ecgdata2.mat % 读入心电图数据
N=length(y); % 数据长度
time=(0:N-1)/fs; % 计算出时间刻度
[x,xtrend]=polydetrend(y, fs, 3); % 用多项式拟合法求出趋势项及消除后的序列
% 作图
subplot 311; plot(time,y,'k')
title('输入心电信号'); ylabel('幅值');
axis([0 max(time) -2000 6000]); grid;
subplot 312; plot(time,xtrend,'k','linewidth',1.5);
title('趋势项信号'); ylabel('幅值');
axis([0 max(time) -2000 6000]); grid;
subplot 313; plot(time,x,'k');
title('消除趋势项心电信号'); ylabel('幅值');
xlabel('时间/s');
axis([0 max(time) -2000 6000]); grid;
set(gcf,'color','w');
3.案例延伸
除了以最小二乘法拟合消除趋势项以外,还有其他方法可以消除趋势项,只是最小二乘法拟合的方法用得较多。其他的方法主要是一些平滑或滤波的方法,只取信号中的低频信号。例如可以用sgolay滤波器求取趋势项。sgolay滤波器是由SavitzkyA和GolayM在1964年提出的一种基于多项式拟合的最佳形式的低通滤波器[23,将在4.5.3小节中详细地说明。下面给出用sgolay滤波器对中的心电图数据消除趋势项的方法。读人已知的心电图ecgdata2.mat数据,用sgolay 滤波器消除基线的漂移。程序清单如下:
clear all; clc; close all;
load ecgdata2.mat % 读入心电图数据
N=length(y); % 数据长度
time=(0:N-1)/fs; % 计算出时间刻度
y1=sgolayfilt(y,3,2001); % 用sgolay滤波器求出趋势项
x=y-y1; % 计算消除趋势项后的序列
% 作图
subplot 311; plot(time,y,'k')
title('输入心电信号'); ylabel('幅值');
axis([0 max(time) -2000 6000]); grid;
subplot 312; plot(time,y1,'k','linewidth',1.5);
title('趋势项信号'); ylabel('幅值');
axis([0 max(time) -2000 6000]); grid;
subplot 313; plot(time,x,'k');
title('消除趋势项心电信号'); ylabel('幅值');
xlabel('时间/s');
axis([0 max(time) -2000 6000]); grid;
set(gcf,'color','w');
寻找信号中的峰值和谷值
MATLAB中峰谷值检测的函数
1.检测峰值的函数
检测峰值的函数是MATLAB自带的,在signal工具箱中
函数:findpeaks功能:寻找待测信号的峰值
调用格式:
pks = findpeaks(x)
[pks,locs] = findpeaks(x)
[pks,locs]=findpeaks(x,'属性',参数)说明:如果只找一个峰值可以用max函数,而需要寻找多个峰值才用本函数findpeaks。输入参数中x是被检测的信号序列,pks是被检测到信号中峰值的幅值,locs是被检测到峰值的位置,是序列的索引号。为了检测到峰值可以设置各种条件,即由属性和对应的参数来限定。可以利用findpeaks函数中的属性和参数较灵活地寻求序列中的峰值,在以下案例中还会介绍利用findpeaks函数来寻找谷值。
2.检测峰值和谷值的函数
本函数检测峰值和谷值,但不是MATLAB自带的,而是由帝国理工学院电气电子工程系的Mike Brookes教授在voicebox中提供的。该函数原名为findpeaks,为了避免和 MATLAB自带的findpeaks混淆,在本书中改名为findpeakm。
所数:findpeakm功能:寻找待测信号的峰值和谷值
调用格式:[K,V]= findpeakm(x,m,w)说明:输入变量x是被测序列;m是方式,选用'g'时是用二次曲线内插后寻找峰值,选用v'时是寻找谷值;w是在寻找峰值时,两个峰值之间最小间隔的样点数。
已知一个脉动信号,如何求信号的周期
1.概 述
在实际信号处理中经常会遇到脉动信号,可通过提取峰值求出峰值间的距离计算出脉动信号的平均周期,如果有谷值的话也可以从谷值间的距离计算出脉动信号的平均周期。在本节中用脉搏信号分别从峰值和谷值位置获取脉动信号的平均周期。
2.实 例
某一患者的脉搏信号在ffpulse.txt文件中,采样频率是200Hz。脉搏不稳定,通过脉搏信号的峰值求出脉搏的平均周期。程序第一部分清单如下:
clear all; clc; close all;
y=load('ffpulse.txt'); % 读入脉搏数据
x=detrend(y); % 消除趋势项
fs=200; % 采样频率
N=length(x); % 数据长度
time=(0:N-1)/fs; % 时间刻度
% 第一部分,用findpeaks函数求峰值位置
[Val,Locs]=findpeaks(x,'MINPEAKHEIGHT',200,'MINPEAKDISTANCE',100);
T1=time(Locs); % 取得脉搏峰值时间
M1=length(T1);
T11=T1(2:M1);
T12=T1(1:M1-1);
Mdt1=mean(T11-T12); % 从峰值得的平均周期值
fprintf('峰值求得的平均周期值=%5.4f\n',Mdt1);
% 作图
pos = get(gcf,'Position');
set(gcf,'Position',[pos(1), pos(2)-100,pos(3),(pos(4)-140)]);
plot(time,x,'k'); hold on; grid;
plot(time(Locs),Val,'ro','linewidth',3);
xlabel('时间/s'); ylabel('幅值'); title('脉搏信号波形图')
set(gcf,'color','w');
% pause
% 第二部分,用findpeakm函数求谷值位置
[K,V]=findpeakm(x,'v',100);
T2=time(K); % 取得脉搏谷值时间
M2=length(T2);
T21=T2(2:M1);
T22=T2(1:M1-1);
Mdt2=mean(T21-T22); % 从谷值得的平均周期值
fprintf('谷值求得的平均周期值=%5.4f\n',Mdt2);
% 作图
plot(time(K),V,'gO','linewidth',3);
set(gcf,'color','w');
如何利用findpeaks 函数求谷值
1.概 述
一般是利用findpeaks函数来寻找峰值,但有时也会利用findpeaks函数来寻找谷值,因为在findpeaks函数中可以设置较多的限制条件,在需要用到这些限制条件会比用findpeakm寻找谷值更有利。
2.实 例
采集到一组数据在文件SDgdata2.mat中,由于外界干扰的原因信号的基线有不规则的漂移,故希望能把基线拉平。读人 SDgdata2.mat文件得到如图4-2-3所示的数据波形图,从图中可看出数据的基线极不规则,下面用找出极小值(谷值点)的方法把基线拉平。

clear all; clc; close all;
load SDqdata2.mat % 读入信号
y=-mix_signal; % 把输入信号反相
% 信号反相后用findpeaks函数检测峰值替代谷值的检测
[Val,Locs]=findpeaks(y,'MINPEAKHEIGHT',-1400,'MINPEAKDISTANCE',5);
b0=interp1(time(Locs),-Val,time); % 延伸谷值,构成基线偏离曲线
x=-y-b0; % 基线拉平的信号
% 作图
subplot 211; plot(time,y,'k'); hold on; grid
plot(time(Locs),Val,'r.','linewidth',3);
xlabel('时间/s'); ylabel('幅值');
title('把信号颠倒过来用寻找峰值替代寻找谷值');
subplot 212; plot(time,x,'k');
xlabel('时间/s'); ylabel('幅值');
title('把基线拉平后的波形图'); grid;
set(gcf,'color','w');
说明:为了能使用findpeaks函数,把读入的信号反相操作,即正值变负值;负值变正值,这样就能用求峰值替代求谷值了。读人的数据mix_signal同样不是一条平滑的曲线,有许许多多的峰值和谷值,为了能获取基线的漂移,必须要适当地选择findpeaks函数中的一些限制参数。在这里选择了MINPEAKIIEIGHT',-1400和MINPEAKDISTANCE',5.从findpeaks函数得到极值点的位置和数值,但这些不是基线的漂移曲线中每一点的位置和数值,而是基线漂移曲线中极值点的位移和数值。通过内插可得到整条基线漂移曲线,再从信号中减去基线漂移,基线基本上得到了校正。
寻找信号中的峰值和谷值
在信号处理中经常会对时间域或频率域的信号提取信号波形的包络,在提取包络后往往还要做进一步处理。提取包络最常用的方法是希尔伯特变换,此外还有其他方法,介绍几种实用的方法。
用希尔伯特变换计算信号的包络
1.概况
在求某一信号包络时用得最多的是希尔伯特变换,但并不是希尔伯特变换适用于所有信号求包络的情况。这是因为对于包络没有一个很严格的定义,在求包络时不同的情况会有不同的要求。本小节介绍用希尔伯特变换求取信号的包络。
2.实例
设信号x(n)=120+96e-(m/1500)cos(2xn/600),n=-5000:20:例4-3-1(pr4 31)5000,求该信号的包络线。设置信号后直接调用hilbert函数求信号的包络,程序清单的第一部分如下:
clear ; clc; close all;
n=-5000:20:5000; % 样点设置
% 程序第一部分:直接做做希尔伯特变换
N=length(n); % 信号样点数
nt=0:N-1; % 设置样点序列号
x=120+96*exp(-(n/1500).^2).*cos(2*pi*n/600); % 设置信号
Hx=hilbert(x); % 希尔伯特变换
% 作图
plot(nt,x,'k',nt,abs(Hx),'r');
grid; legend('信号','包络');
xlabel('样点'); ylabel('幅值')
title('信号和包络')
set(gcf,'color','w');
% 程序第二部分:消除直流后做希尔伯特变换
y=x-120; % 消除直流分量
Hy=hilbert(y); % 希尔伯特变换
% 作图
figure(2)
plot(nt,y,'k',nt,abs(Hy),'r');
grid; legend('信号','包络');
xlabel('样点'); ylabel('幅值')
title('信号和包络')
set(gcf,'color','w');
figure(3);
plot(nt,x,'k',nt,abs(Hy)+120,'r');
grid; legend('信号','包络'); hold on;
xlabel('样点'); ylabel('幅值')
title('信号和包络')
set(gcf,'color','w');
% 程序第三部分:通过频域做希尔伯特变换
y_fft=fft(y); % FFT
y_hit(1)=y_fft(1); % 按式(4-3-11)设置y_hit
y_hit(2:(N+1)/2)=2*y_fft(2:(N+1)/2);
y_hit((N+1)/2+1:N)=0;
z=ifft(y_hit); % 对y_hit做IFFT
% 作图
figure(4)
subplot 211; plot(n,real(Hy),'r',n,real(z),'g');
xlabel('样点'); ylabel('幅值'); legend('时域','频域')
title('频域和时域希尔伯特变换实部比较');
subplot 212; plot(n,imag(Hy),'r',n,imag(z),'g');
xlabel('样点'); ylabel('幅值'); legend('时域','频域')
title('频域和时域希尔伯特变换虚部比较');set(gcf,'color','w');
figure(5)
plot(nt,x,'k',nt,abs(z)+120,'r');
grid; legend('信号','包络');
xlabel('样点'); ylabel('幅值')
title('信号和包络')
set(gcf,'color','w');
用求极大值和极小值的方法来计算信号的包络线
1.概 述
指出用hilbert函数求包络线不一定适用于所有的信号,有时对包络线的要求也不完全相同,所以在某些情况下可以用极大值,、极小值的方法来求取信号的包络线。
2.案例分析
从文件pulsedata0.txt中读出脉冲信号,求取该脉冲信号的上、下包络线。本例将分为两部分:第一部分用hilbert函数求包络线,第二部分用极大值、极小值的方法来求取包络线。程序第一部分清单如下:
clear all; clc; close all;
xx=load('pulsedata0.txt'); % 读入信号
N=length(xx); % 数据长度
n=1:N; % 设置样点序列
% 作图
plot(n,xx,'k'); grid;
xlabel('样点'); ylabel('幅值');
title('原始信号波形图')
set(gcf,'color','w');
% 程序第一部分用hilbert计算信号的包络
xm=sum(xx)/N; % 计算信号的直流分量
x=xx-xm; % 消除直流分量
z=hilbert(x); % 进行希尔伯特变换
% 作图
figure(2)
plot(n,x,'k'); hold on; grid;
plot(n,abs(z),'r');
xlabel('样点'); ylabel('幅值');
title('消除直流分量用求取包络曲线图')
set(gcf,'color','w');
% 程序第二部分用求极大极小值计算信号的包络
% 利用findpeakm函数计算信号的极大极小值
[K1,V1]=findpeakm(x,[],120); % 求极大值位置和幅值
up=spline(K1,V1,n); % 内插,获取上包络曲线
[K2,V2]=findpeakm(x,'v',120);% 求极小值位置和幅值
down=spline(K2,V2,n); % 内插,获取下包络曲线
% 作图
figure(3)
plot(n,x,'k'); hold on; grid;
plot(n,up,'r');
plot(n,down,'r');
xlabel('样点'); ylabel('幅值');
title('用求取极大极小值方法获取包络曲线图')
set(gcf,'color','w');


用倒谱法来计算语音信号频谱的包络线
1.概述
语音信号频谱的包络线对语音分析来说是比较重要的,它反映了人类发声器官的共振结构,从频谱的包络可提取共振峰参数(频率和带宽)。在语音分析中常用倒谱方法来提取语音信号频谱的包络线。


clear all; clc; close all;
y=load('su1.txt'); % 读入数据
fs=16000; nfft=1024; % 采样频率和FFT的长度
time=(0:nfft-1)/fs; % 时间刻度
nn=1:nfft/2; ff=(nn-1)*fs/nfft; % 计算频率刻度
Y=log(abs(fft(y))); % 取幅值的对数
z=ifft(Y); % 按式(4-3-16)求取倒谱
mcep=29; % 分离声门激励脉冲和声道冲击响应
zy=z(1:mcep+1);
zy=[zy' zeros(1,1024-2*mcep-1) zy(end:-1:2)']; % 构建声道冲击响应的倒谱序列
ZY=fft(zy); % 计算声道冲击响应的频谱
% 作图
plot(ff,Y(nn),'k'); hold on; % 画出信号的频谱图
plot(ff,real(ZY(nn)),'k','linewidth',2.5); % 画出包络线
grid; hold off; ylim([-4 5]);
title('信号频谱和声道冲击响频谱(频谱包络)')
ylabel('幅值'); xlabel('频率/Hz');
legend('信号频谱','频谱包络')
set(gcf,'color','w');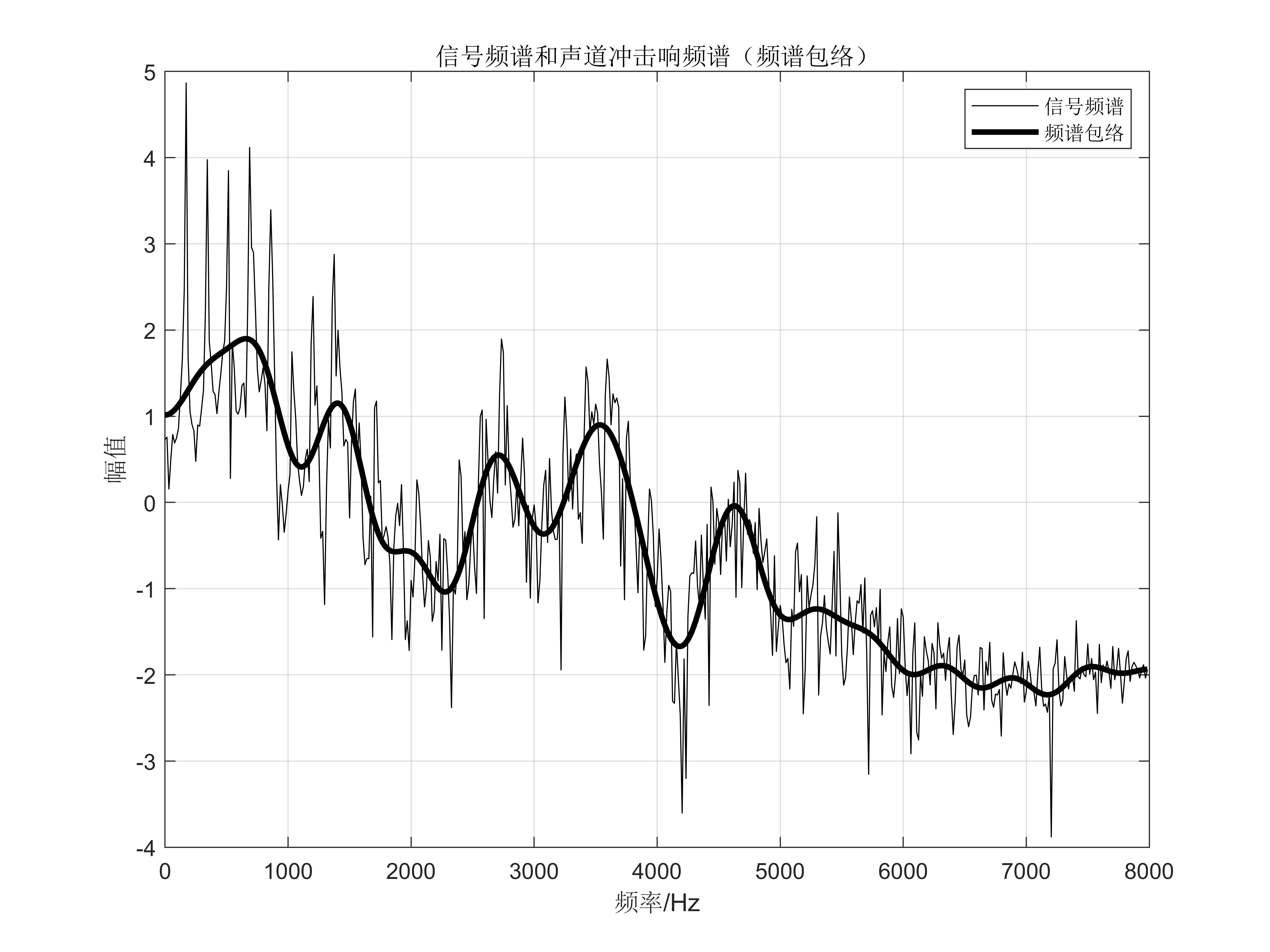
获取代码请关注MATLAB科研小白的个人公众号(即文章下方二维码),并回复信号处理中简单实用的方法本公众号致力于解决找代码难,写代码怵。各位有什么急需的代码,欢迎后台留言~不定时更新科研技巧类推文,可以一起探讨科研,写作,文献,代码等诸多学术问题,我们一起进步。