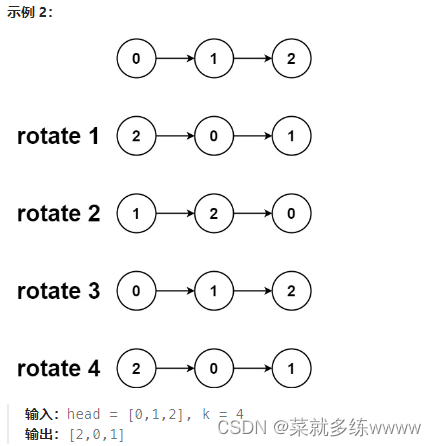
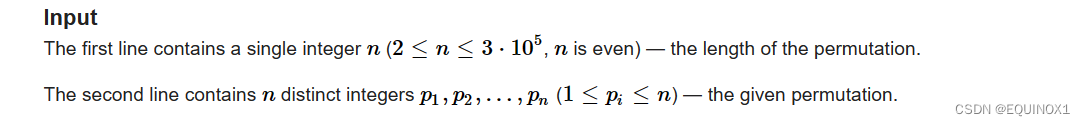一、题目

1、题目描述

2、输入输出

2.1输入

2.2输出

3、原题链接

Problem - 1148C - Codeforces

---

二、解题报告

1、思路分析

题目提示O(5n)的解法了，事实上我们O(3n)就能解决，关键在于1，n的处理

我们读入数据a[]，代表初始数组，p[i]代表 i 的下标

如果p[i] != i

说明需要交换

a[p[i]] 一定能跟a[1]或者a[n]交换, a[i]也一定能跟1或n交换

假设 a[i]  的可交换位置为x，a[p[i]] 的可交换位置为y（x、y只可能为1、n）

那么我们使得元素i从p[i] -> y -> x -> i 就在3步之内让i到达了下标i

此时a[1] 和 a[n]可能不满足a[1] = 1, a[n] = n

事实上我们将每个元素调整完后再调整1和n即可

这也是为什么能从O(5n)优化到O(3n)

 

2、复杂度

时间复杂度： O(3n)空间复杂度：O(n)

3、代码详解

​

#include <bits/stdc++.h>
using PII = std::pair<int, int>;
const int N = 3e5 + 10;
int p[N], a[N], n, s;
std::vector<PII> path;void swap(int x, int y) {std::swap(p[a[x]], p[a[y]]);std::swap(a[x], a[y]);path.emplace_back(x, y);
}int main () {std::cin >> n;path.reserve(5 * n);for (int i = 1; i <= n; i ++ ) std::cin >> a[i], p[a[i]] = i;for (int i = 1; i <= n / 2; i ++ ) {if (p[i] != i) {if (p[i] <= n / 2) {swap(p[i], n);swap(i, n);}else {swap(1, p[i]);swap(1, n);swap(i, n);}}}for (int i = n / 2 + 1; i <= n; i ++ ) {if (p[i] != i) {if (p[i] > n / 2) {swap(1, p[i]);swap(1, i);}else {swap(p[i], n);swap(1, n);swap(1, i);}}}if (a[1] != 1) swap(1, n);std::cout << path.size() << '\n';for (auto [x, y] : path) std::cout << x << " " << y << '\n';return 0;
}