题目描述
每一头牛的愿望就是变成一头最受欢迎的牛。现在有 N 头牛,给你 M 对整数,表示牛 A 认为牛 B 受欢迎。这种关系是具有传递性的,如果 A 认为 B 受欢迎,B 认为 C 受欢迎,那么牛 A 也认为牛 C 受欢迎。你的任务是求出有多少头牛被除自己之外的所有牛认为是受欢迎的。
输入描述
第一行两个数 N,M;
接下来 M 行,每行两个数 A,B,意思是 A 认为 B 是受欢迎的(给出的信息有可能重复,即有可能出现多个 A,B)。
输出描述
输出被除自己之外的所有牛认为是受欢迎的牛的数量。
样例输入
3 3 1 2 2 1 2 3
样例输出
1
我们先把这道题分成两种情况来讨论
第一种情况:不存在环
首先来画一个图

观察一下每个点的出度
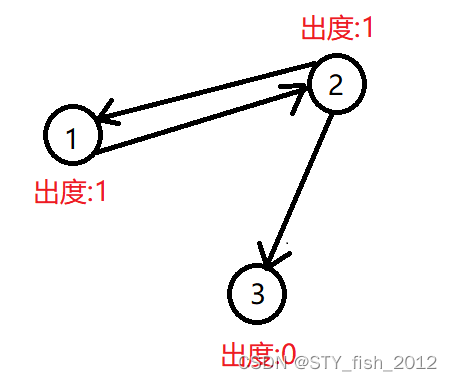
在这幅图中,最受欢迎的牛是3, 那么,是否是出度为零的点就最受欢迎呢?
再来看一下

此时,点4的出度也为零,但是,这张图没有最受欢迎的牛,因为条件是除自己以外,所有人都认为它受欢迎才行,所以,在没有环情况下,如果只有一个出度为零的点,就有一头最受欢迎的牛,否则一头都没有
再来看第二种情况
第二种情况:存在环
还是来画张图
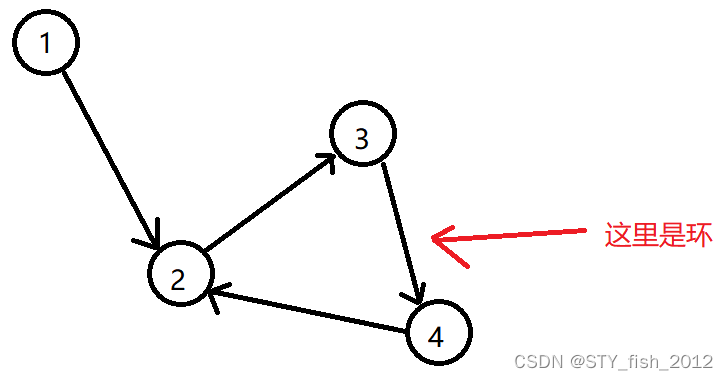
这里最受欢迎的是2,3,4
结论:有环时,先把每一个环合并成一个点,在按照没有环的方案去找,最后最受欢迎的就是那个点合并前的所有点
#include<bits/stdc++.h>
using namespace std;
const int N=1e4+5;
vector<int>a[N];
int dfn[N],vis[N],id[N],size[N],low[N],cd[N];
int n,m;
int times;
int scc;
stack<int>t;
void tarjan(int x){vis[x]=1;dfn[x]=low[x]=++times;t.push(x);for(int i=0;i<a[x].size();i++){int v=a[x][i];if(dfn[v]==0){tarjan(v);low[x]=min(low[x],low[v]);}else if(vis[v]==1){low[x]=min(low[x],dfn[v]);}}if(low[x]==dfn[x]){scc++;int v;do{v=t.top();t.pop();vis[v]=0;id[v]=scc;size[scc]++;}while(x!=v);}
}
main(){scanf("%d%d",&n,&m);for(int i=1;i<=m;i++){int u,v;scanf("%d%d",&u,&v);a[u].push_back(v);}for(int i=1;i<=n;i++){if(dfn[i]==0)tarjan(i);}for(int x=1;x<=n;x++){for(int i=0;i<a[x].size();i++){int v=a[x][i];int u1=id[x];int u2=id[v];if(u1!=u2){cd[u1]++;}}}int cnt=0,ans=0;for(int i=1;i<=scc;i++){if(cd[i]==0){ans+=size[i];cnt++;if(cnt>1){printf("0");return 0;}}}printf("%d",ans);
}